- 九九が十分に覚え切れていない.したがって,因数分解のときに,例えば掛けて 24 になるような2つの数が見つけられない.
- 正負の足し算,引き算のルールが定着できていない.例えば,異符号の足し算のときは,絶対値の引き算の計算をしなければならないが,足し算なのに引き算をしなければならないことにとまどってしまう(1-3 の計算を 4 または -4 としてしまう).
- 分数の計算が苦手である.約分の原理は理解しているが,3 や 7 などの数で割るものは九九が不十分なため手が止まってしまう(
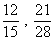 など).また,通分がまったくわかっていない者もわずかながらいる.
など).また,通分がまったくわかっていない者もわずかながらいる.
ちなみに私が受け持つクラスの入試の平均点は60点満点で14.0点(23.3%)であった.
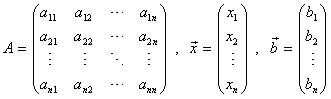 とする.
とする.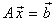 の解は, det A ≠0 のときただ一組の解を持ち,その解は
の解は, det A ≠0 のときただ一組の解を持ち,その解は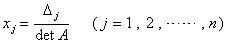
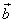 で置き換えた行列式である.
で置き換えた行列式である.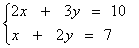 i.e.
i.e. 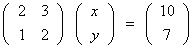
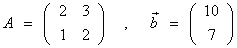 とおき,A の第1列,および第2列を
とおき,A の第1列,および第2列を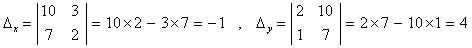
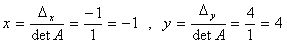 ……(答)
……(答)
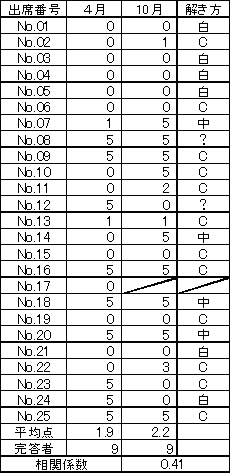 (問題)
(問題)