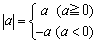斵傜偼側偤乥x乥亙1 傪x亙亇1偲偡傞偺偐丠
嶥杫埉媢崅峑丂拞懞暥懃
丂尰壽掱偵偍偄偰愨懳抣偺巜摫偼丆戝偒側娭栧偲側偭偰棫偪偼偩偐偭偰偒偰偄傞丏
丂偦傟偼晄摍幃偺奣擮偑拞妛偐傜崅峑傊堏峴偟偰偒偨偙偲傕梫場偱偁傝丆惗搆偵偲偭偰偼晄摍幃偑傑偩乽楙傜傟偰偄側偄乿偆偪偵丆偦偺墳梡偱偁傞愨懳抣偑廝偄偐偐偭偰偔傞偺偱偁傞丏妋偐偵 傛偆側夝摎偼愄傕偢偄傇傫偁偭偨偑丆尰壽掱偵側偭偰偐傜偼恖悢偑寖憹偟丆嬃偒偲(嫵巘偲偟偰偺)幐堄偺擮傪姶偠偰偟傑偆偺偩丏
丂偙偺傛偆側夝摎偵懳偟偰偼丆偄傑傑偱偼丆
乽壗傗偭偰傫偩丆偙傫側夝摎偼恖娫偲偟偰嫋偝傟側偄偩傠丏愨懳傗傞側丏崱搙傗偭偨傜妎屽偟偰偍偗傛乿
偲丆攍鎖嶨尵傪梺傃偣丆嫼偟傪偐偗偰嵪傑偣偰偟傑偭偰偄偨偑丆偙傟偩偗棟夝偱偒側偄傕偺偑偄傞偲丆斵傜偺怱棟暘愅偲崌傢偣偰偦偺棟桼傪抦傝偨偔側傞丏彮偟扵偭偰傒傛偆丏
丂傑偢丆斵傜偼乥x乥=1傪偳偆懆偊偰偄傞偺偩傠偆偐丏
丂拞妛偱偼丆斵傜偼愨懳抣傪乽尨揰偐傜偺嫍棧乿偲偟偰嫵偊傜傟傞丏偟偨偑偭偰丆乥x乥=1偼丆
乽尨揰偐傜偺揰x傑偱偺嫍棧偑1偵摍偟偄乿
偲傒側偟丆偦偺抣傪尨揰偐傜x幉忋嵍塃偺曽岦偵墑偽偟x=亇a偲偡傞丏曄悢x偲嵍曈偺嫍棧1傪斾妑偟側偑傜偦偺抣傪應傞偺偱偁傞丏摨條偵峫偊傞偲丆乥x乥亙1偼丆
乽尨揰偐傜揰 傑偱偺嫍棧偑1傛傝抁偄乿
偲偟丆x傪應傞偲丆-1亙x亙1偲側傞偼偢側偺偩偑丆偙偙偱晄摍幃偺奣擮偑掕拝偟偰偄側偄斵傜偺巚峫偼旘傇丏
丂扨弮偵x偲塃曈偺1傪斾妑偟丆嫍棧偑1偺揰x偺抣傪亇1偲媮傔丆椉幰傪寢傇晄摍崋傪戝偟偰峫偊傕偣偢偵(峫偊傞偙偲傕偱偒側偔) 幚偵埨捈偵丆x亙亇1偲寢榑傪堷偒弌偡偺偱偁傞丏
丂愨懳抣偺嫍棧揑懆偊偼崅峑偺悢妛嘥偵傕堷偒宲偑傟偰丆嫍棧傪応崌暘偗偡傞偙偲偱愨懳抣偼師偺傛偆偵掕媊偝傟傞丏
丂丂丂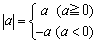
丂偙傟傪娙棯壔偡傞偲丆乥a乥=亇a偲側傞偑丆偙偙偱巊傢傟傞摍崋(=)偼嵍曈偺愨懳抣偺寢壥傪昞偡傕偺偱偁傝丆偦偺抣偑塃曈偺亇a偱偁傞偲偄偆偙偲偱偁傞丏偟偐偟丆偙傟偵懳偟偰乥x乥=k (k亜0)偱偁傞幃偼丆乥x乥偑塃曈偺k偵摍偟偄x偺抣偼壗偐傪梫媮偟丆偦偺寢壥偲偟偰x=亇k偑摼傜傟偰偄傞丏峆摍幃丒曽掱幃偺堘偄偱椉幰偺摍崋偺巊傢傟曽偼堎側偭偰偄傞偺偩丏
丂偩偐傜乥x乥=k偺愨懳抣傪嫍棧揑側埖偄偲偟偰懆偊丆偦偺戝偒偝傪昡壙偡傞偺偱偁傟偽丆
丂丂丂乥x乥=k丂佀丂x=亇k
偲側傞丏偟偐偟丆乽愨懳抣傪偼偢偡乿偙偲偱夝偔偺偱偁傟偽丆
丂丂丂乥倶乥=k丂佀丂亇x=k
偲偡傋偒偱偁傞丏偟偐偟偙偺摍幃亇x=k偼丆x=亇k偲側傞偐傜丆嫍棧揑夝朄偲姶妎揑偵偼摨偠傛偆偵巚傢傟丆偦偺嫇嬪丆姩堘偄偟偰偟傑偭偨斵傜偼丆偦偺傑傑晄摍幃偵傕摉偰偼傔傛偆偲偡傞丏偙傟偑丆
丂丂丂乥x乥亙1丂佀丂x亙亇1
偲偟偰偟傑偆斵傜偺敪憐側偺偱偁傞丏
丂偩偑丆幚嵺偵丆乽愨懳抣傪偼偢偡乿偙偲偱晄摍幃傪夝偔偲丆
丂丂丂乥x乥亙1丂佀丂亇x亙1
偱偁傞偐傜丆亅x亙1傛傝丆-1亙x偑摼傜傟丆x亙1偺幃偐傜丆
丂丂丂-1亙x亙1丂丂乧乧嘆
偲側傞偺偩傠偆偐丏
丂傕偪傠傫偙傟偼岆偭偨夝摎偱偁傞丏偟偐偟丆x亙亇1偼夝摎偺嫅愨埲奜偺側偵傕偺偱傕側偄偑丆亇x亙1偼丆乽応崌暘偗乿偄偆廳梫側奣擮偵堷偒宲偑傟偰偄偔丏
丂嘆偺夝摎偺岆傝偼丆-1亙x偲x亙1偺嫟捠夝傪媮傔偰偟傑偭偨偙偲偱偁傞丏杮棃偼応崌暘偗偟偨斖埻偺榓廤崌傪夝偲偡傞傢偗偩偐傜丆偙偺曽朄偱夝偄偰偟傑偆偲杮摉偼偡傋偰偺幚悢偑夝偲側偭偰偟傑偆丏嘆偺夝朄偼俀廳偺岆傝傪斊偟偰偄傞偺偩丏
丂斵傜偑晄摍幃傪嬯庤側傕偺偲姶偠傞偺偼丆嫟捠晹暘傪偄偭偰偄傞偐丆擇偮埲忋偺斖埻偺晹暘傪崌傢偣傛偆偲偟偰偄傞偺偐丆偦偺堘偄偑偼偭偒傝偲暘偐傜側偄偙偲偵傕尨場偑偁傞丏斵傜偺懡偔偼応崌暘偗傪偡傞偲偒偵丆偳偆偄偭偨斖埻(group)偱暘偗偰偄傞偐偑偄偮偺娫偵偐寚棊偟偰偟傑偆丏愨懳抣偼丆偦偺抣偑侽傪嫬偲偟偰惓丒晧偺応崌偱偼偢偡偑丆乥x乥=1傪夝偔偲偒偵偼丆愨懳抣傪嫍棧揑奣擮偲崿摨偟側偑傜丆懄嵗偵偼偢偟偰x=亇k偲敾抐偟偰偟傑偄丆寢壥丆偡傋偰偺愨懳抣偵懳偟偰傕摨偠偙偲偑偱偒傞偲奼戝夝庍傪偟偰偟傑偆偺偱偁傞丏偦偆偄偭偨揰偱傕丆偙偺亇x=1偐傜師偺棳傟傪嶌偭偰偄偔偙偲偑丆応崌暘偗巜摫偺嵟揔側僠儍儞僗摓棃偱偁傞偲峫偊傞傋偒側偺偱偁傞丏
丂偩偐傜丆乥x乥=-1偺傛偆側栤戣傪採帵偟丆嫍棧揑側奣擮偱夝偑側偄偙偲傪愢柧偟偨屻偵丆愨懳抣偺偼偢偡偙偲傪応崌暘偗傪偟側偑傜夝偄偰傒偰傕傛偄丏
丂x亙0偺偲偒偼丆-x亖-1傛傝x=1丏
丂丂偙傟偼丆x亙0傛傝晄揔丏
丂0亝x偺偲偒偼丆x=-1丏
丂丂偙傟偼丆0亝x傛傝晄揔丏
丂柧傜偐偵夝偑側偄偙偲傪柧傜偐偱側偄傛偆偵愢柧偡傞偙偲傕昁梫側偙偲偱偼側偄偩傠偆偐丏
丂偝偰丆乥x乥亙1偺夝傕丆摨條偵丆
丂x亙0偺偲偒偼丆-x亙1傛傝丆-1亙x丏
丂丂傛偭偰嫟捠斖埻傪媮傔偰丆-1亙x亙0丏
丂0亝x偺偲偒偼丆x亙1丏
丂丂傛偭偰嫟捠斖埻傪媮傔偰丆0亝x亙1丏
丂埲忋傛傝丆俀偮偺夝傪崌傢偣偰-1亙x亙1
偲側傞丏
丂偙偆偄偭偨婎杮揑側夝摎偺棳傟偑丆墳梡揑側栤戣偺戝偒側夝摎偺棳傟偵側偭偰偄偔偺偱偁傞丏
丂偱偼丆斵傜偵懳偟偰変乆偼偳偆懳墳丆懳張偡傋偒偐偲偄偆尰幚偺栤戣傪峫偊傛偆丏
丂傑偢丆傂偲偮偵偼丆変乆偼愨懳抣偺俀柺惈傪偒偪傫偲愢柧偡傋偒偱偁傞偲巚偆丏偦偺偨傔偵偼晧晞崋偺俀柺惈偵偮偄偰傕愢柧傪帋傒側偗傟偽側傜側偄丏晧晞崋乽亅乿偼偦傟偑偮偔抣偑晧悢偱偁傞偙偲偲丆偦傟偑偮偔抣偺晞崋傪僠僃儞僕(曄姺)偡傞嶌梡慺揑側摥偒傪傕偮丏-a偺応崌偼屻幰偺堄枴偱偁傝丆偙傟偑愨懳抣傪偼偢偡幚嵺偺嶌嬈偱偁傞傢偗偩丏
丂傕偆傂偲偮偼丆嫵壢彂偵偼嫍棧揑側堄枴偐傜
丂丂丂乥x乥=k丂佀丂x=亇k
偑採帵偝傟丆偦傟偱廔傢偭偰偟傑偭偰偄傞丏偙傟偑x亙亇k偲偄偆夝摎傪嶌傝弌偡尦嫢偵側偭偰偄傞偲偄偆偙偲傪摜傑偊丆偦偺偆偊偱愨懳抣偺奜偟曽偺愢柧偑側偝傟傞傋偒偱偁傞丏
丂偨偩丆愨懳抣偺嫍棧揑夝朄偑晄梫偲偄偆偙偲偱偼側偄丏愨懳抣偺夝朄帺懱偑偙偺屻丆僌儔僼忋偺娭悢偲偟偰懆偊傜傟偰偄偔偐傜丆乽偼偢偟曽乿傪巜摫偡傞偙偲傕娷傔丆抜奒揑側儗儀儖偱敪憐傪攟偭偰偄偗偽傛偄丏戝帠側偙偲偼丆愨懳抣偺偼偢偟曽偑崅峑悢妛偱斵傜偑懳洺偡傞弶傔偰偺乽応崌暘偗乿偱偁傝丆変乆偵偲偭偰偼巜摫偺岲婡偱偁傞偲偄偆偙偲偩丏偙偙偱忳偭偰偟傑偆偲斵傜偺榑棟揑巚峫偺敪夎偑抶傟偰偟傑偆偺偱偁傞丏