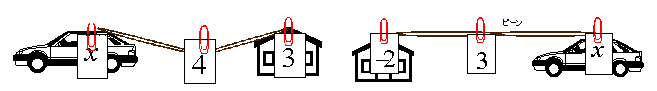嶥杫憯娾崅峑丂拞懞丂暥懃


 亂嵽丂椏亃丂杮帪偱巊梡偡傞慺嵽
亂嵽丂椏亃丂杮帪偱巊梡偡傞慺嵽
岤巻丄嫵幒偺暻偵揬偭偰偁傞晄梫偵側偭偨宖帵暔(惣梞巻)丄僠儑乕僋(偁傞偄偼儅僕僢僋)丄僴僒儈丄儅僌僱僢僩丄椫僑儉丄僋儕僢僾亂壓偛偟傜偊亃
岤巻傪愗傝敳偄偰丄帺摦幵丄壠傪嶌傞丅嫵幒偺晄梫偺宖帵暔傪攓庁偟偰丄僇乕僪傪嶌傞丅
亂挷丂棟亃
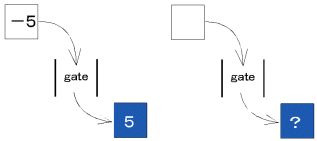 乻婎杮曇1乼丂丂乣僇乕僪偺抣偐傜愨懳抣傪儊僀僋傞
乻婎杮曇1乼丂丂乣僇乕僪偺抣偐傜愨懳抣傪儊僀僋傞
- 愨懳抣傪昞偡婰崋| |偼丄悢偺戝偒偝傪媮傔傞偨傔偺gate偱偁傞偙偲傪愢柧丅
- 崟斅偵愨懳抣婰崋傪彂偒丄惣梞巻傪愗傝敳偄偰嶌偭偨僇乕僪偑愨懳抣gate傪偔偖傞偲偳偆側傞偐梊憐偝偣傞丅
- 敀巻偺僇乕僪偼gate傪捠偡偲偳偆側傞偐峫偊傞丅
- 敀巻偺僇乕僪偵 偲彂偒丄gate傪捠偡偲偳偆側傞偐挷傋傞丅
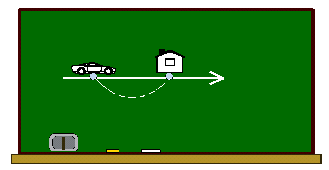
乻婎杮曇2乼丂丂乣帺摦幵傪憱傜偣愨懳抣傪儊僀僋傞
- 悢捈慄忋偱
丂丂丂(幵偺埵抲)亅(壠偺埵抲)亖(幵偲壠偺嫍棧)
偱偁傞偙偲傪愢柧丅偙偙偱丄(幵偺埵抲)亙(壠偺埵抲)丂偺偲偒丄嫍棧亙侽丂偲側傞丅 - 偦偙偱丄(嫍棧)亞侽偲偡傞偨傔偵丄乥丂丂乥傪偮偗偰廋惓偡傞偙偲傪愢柧丅
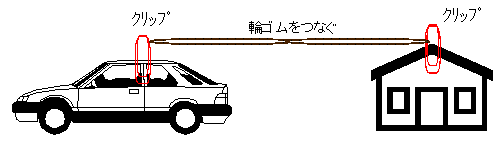
- 僋儕僢僾偲椫僑儉偱岤巻偱嶌偭偨壠偲幵傪寢傇丅
- 椫僑儉偑抩傫偱偄側偄挿偝偑愨懳抣偺抣偱偁傞偙偲傪愢柧偡傞丅
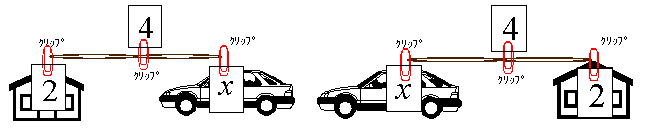
乻婎杮曇3乼丂丂乣幵偲壠偺嫍棧偐傜愨懳抣侾師曽掱幃傪儊僀僋傞
ex1) 師偺曽掱幃傪夝偗丅
丂丂丂(1) 乥x-2乥=4丂丂(2)乥x乥=3丂丂(3) 乥2x-3乥=4 |
- x 丆2丆4傪彂偄偨俁枃偺僇乕僪傪梡堄偟丄偦傟偧傟丄幵丄椫僑儉丄壠偵肛邆艐矀迊B
- 丒僑儉傪抩傑側偄忬懺偵偟偨偲偒偺壠偐傜幵傑偱偺嫍棧傪媮傔傞丅丂
- 丒摨條偵(2)偵偮偄偰偼乥x-0乥=3 偲峫偊丄傑偨(3)偵偮偄偰偼 乥x-3/2乥=2 偲峫偊昁梫側僇乕僪傪梡堄偡傞丅
乻婎杮曇4乼丂丂乣幵偲壠偺嫍棧偐傜愨懳抣侾師晄摍幃傪儊僀僋傞
ex1) 師偺晄摍幃傪夝偗丅
丂丂丂(1) 乥x-3乥亙4丂丂(2)乥x+2乥亜3丂丂(3) 乥3x+2乥亞1 |
- x丆3丆4偲彂偄偨俁枃偺僇乕僪傪梡堄偟丄偦傟偧傟肛邆艓詠A椫僑儉丄壠偵嫴傓丅
- 僑儉傪抩傫偩忬懺偵偟偨偲偒偺幵偲壠偺嫍棧偺曄壔傪撉傒庢傞丅
- (2) 乥x-(-2)乥亜3偲傒偰丄 x丆-2丆3傪彂偄偨僇乕僪傪梡堄偟丄幵丄椫僑儉丄壠偵嫴傓丅
- 椫僑儉傪抩傑側偄忬懺偐傜怢偽偟丄壠偐傜幵傑偱偺嫍棧傪撉傒庢傞丅
- (3) 乥x+2/3乥亞1/3 偲偟偰昁梫側僇乕僪傪梡堄偟丄(2)偲摨條偺憖嶌傪偡傞丅
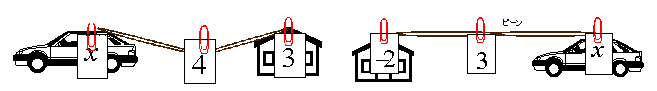
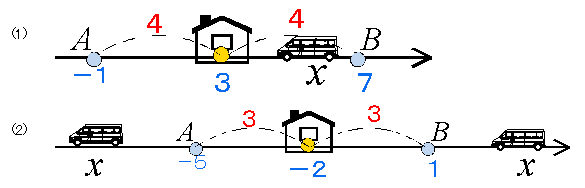
乻墳梡曇1乼丂丂乣悢捈慄忋偵愨懳抣曽掱幃傪儊僀僋傞
ex1)偺(1)偺栤戣傪夝偔丅- 崟斅偵悢捈慄傪彂偔丅
- 弌敪揰偱偁傞 x=2 偺応強偵儅僌僱僢僩偱壠傪揬傞丅
- 壠偐傜偺嫍棧偑4偱偁傞悢捈慄忋偺揰偵儅僌僱僢僩偱幵傪揬傞丅
- 幵偺埵抲傪撉傒庢傞丅

乻墳梡曇2乼丂丂乣悢捈慄忋偵愨懳抣晄摍幃傪儊僀僋傞
ex2)偺(1)偺栤戣傪夝偔丅- 崟斅偵悢捈慄傪彂偔丅
- x=3 偺応強偵儅僌僱僢僩偱壠傪揬傞丅
- 壠偐傜偺嫍棧偑係偱偁傞俀揰 A丆B (A亙B) 傪媮傔偦偺嵗昗傪悢捈慄偵彂偔丅
- 壠偐傜幵傑偱偺嫍棧偑係傛傝抁偔側傞傛偆幵傪憱傜偣丄揔摉側応強侾偮偵儅僌僱僢僩偱揬傞丅
- 悢捈慄忋嵍偐傜丄A亙幵亙B 偺弴偵偦偺嵗昗傪彂偔丅
ex2)偺(2)偺栤戣傪夝偔丅- 壠偐傜偺嫍棧偑俁偲側傞俀揰 A丆B 傪媮傔偰偐傜丄嫍棧偑俁傛傝挿偔側傞俀偮偺応強偵幵偺儅僌僱僢僩傪偼傞丅
- 嵍偐傜弴偵 幵亙A丆B亙幵 偺弴偵彂偄偰偄偔丅
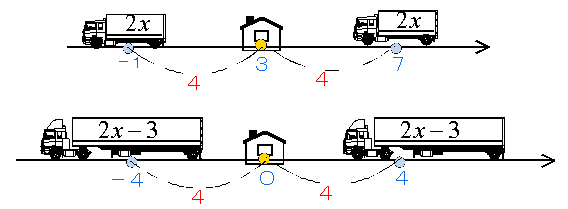
乻墳梡曇3乼丂丂乣幵傪懼偊偰愨懳抣曽掱幃傪儊僀僋傞
ex1) (3)傪夝偔丅- 僇乕僪偵 2x 傪彂偒丄幵偵揬傞(彫宆僩儔僢僋僒僀僘偵偡傞)丅
- 2x 偲偄偆幵庬偺幵偲壠偺埵抲俁傑偱偺嫍棧偑係偺俀揰 A丆B傪媮傔丄偦偺嵗昗傪彂偔丅
- 俀揰 偺埵抲偵幵傪儅僌僱僢僩偱揬傞丅
- 幵偲埵抲 A丆B 傪斾妑偟偰x 偺抣傪媮傔傞丅
丂丂丂2x=-1丆7 傛傝丄x=-1/2丆7/2 - 師偵僇乕僪偵 2x-3 偲彂偒丄幵偵揬傞(戝宆僩儔僢僋僒僀僘偵偡傞)丅
- 2x-3 偲偄偆幵庬偺幵偲壠偺埵抲(尨揰)傑偱偺嫍棧偑係偱偁傞俀揰 傪媮傔傞丅
- A丆B 偺埵抲偵幵傪儅僌僱僢僩偱揬傝丄x 偺抣傪媮傔傞丅
丂丂丂2x-3=-4丆4傛傝丄x=-1/2丆7/2
乻墳梡曇4乼丂丂乣幵傪懼偊偰愨懳抣晄摍幃傪儊僀僋傞
ex2) (1)傪夝偔丅- 僇乕僪偵 x-3 傪彂偒丄幵偵揬傞(戝宆僩儔僢僋僒僀僘偵偡傞)丅
- 壠偺偁傞尨揰偐傜偺嫍棧偑係偱偁傞俀揰 A丆B傪媮傔傞丅
- 僩儔僢僋偲壠偲偺嫍棧偑係傛傝抁偄応強偵僩儔僢僋傪揬傞丅
- A亙僩儔僢僋亙B 偺弴偵彂偔丅
- x偺抣傪媮傔傞丅
丂丂丂-4亙x-3亙4傛傝丄-1亙x亙7
 ex2) (3)傪夝偔丅
ex2) (3)傪夝偔丅- 僇乕僪偵 3x+2 傪彂偒丄幵偵揬傞(戝宆僩儔僢僋僒僀僘偵偡傞)丅
- 壠偺偁傞尨揰偐傜偺嫍棧偑侾偱傞偁傞俀揰 A丆B傪媮傔傞丅
- 僩儔僢僋偲壠偲偺嫍棧偑侾傛傝挿偄応強乮俀売強乯偵僩儔僢僋傪揬傞丅
- 僩儔僢僋亙A丆B亙僩儔僢僋 偺弴偵彂偔丅
- x 偺抣傪媮傔傞丅
丂丂丂3x+2亝-1丆1亝3x+2 傛傝丄x亝-1丆-1/3亝x - 師偵丄僇乕僪偵 3x 偲彂偒丄幵偵挘偭偰摨條偵媮傔偰傒傞(彫宆僩儔僢僋僒僀僘偵偡傞)丅丂丂丂3x亝-3丆-1亝3x傛傝丄x亝-1丆1/3亝x
傑偲傔
丂愨懳抣栤戣偑擄偟偄偺偼丄乽愨懳乿偲偄偭偰偍偒側偑傜丄偦偺夝朄偑乽憡懳乿揑偱偁傞偐傜偩偲巚偄傑偡丅戝偒偝傪媮傔傞婰崋偲懆偊偨傝丄悢捈慄(暯柺丒嬻娫)偵偍偗傞嫍棧偲峫偊偨傝丄偁傞偄偼暯柺忋偺僌儔僼偱偼 幉偵娭偡傞斀幩偲傒偨傝丄埖偆栤戣偵傛偭偰懡庬懡條偺怓傪傒偣傑偡丅傕偪傠傫崻尮偵堘偄偼側偄偺偱偡偑乽偦偆峫偊傞偲暘偐傝堈偄偐傜乿偲墴偟晅偗傞偙偲偑暘偐傝偵偔偔側偭偰偄傞暘栰偺戙昞椺偲偄偊傞偱偟傚偆丅愨懳抣暘栰偑怺傒偵偼傑傞偲嵺尷側偔棊偪崬傓偺偼丄夁嫀偵彫庤嬈僔儕乕僘偱愨懳抣晄摍幃傪埖偭偨偲偒丄師偺晄摍幃曄宍偼擣傔傜傟傞偐偲偄偆偙偲偵懳偟偰偺攇栦偺戝偒偝偐傜傕暘偐傝傑偡丅
丂丂丂嘆乥2x-1乥亙x丂佁丂-x亙2x-1亙x
丂丂丂嘇乥2x-1乥亜x丂佁丂2x-1亙-x丆x亙2x-1
丂幚偼椉曽偲傕偵惓偟偄偙偲偑僱僢僩忋偺媍榑偱徹柧偝傟偨偺偱偡偑丄嘇偵懳偟偰偼惓偟偄偺偵側偤尰応偱偼擣傔傜傟側偄偐偲偄偆揰偱偼埶慠寢榑偑偱偰偄傑偣傫丅愨懳抣偼悢妛揑偵怗傟傜傟偨偔側偄晹暘傪旐暍偟偰偄傞gate傒偨偄側傕偺偱傕偁傝丄偦偙偼嫵堢忋丄僱僌儗僋僩偟偨曽偑偒偭偲偄偄偺偱偟傚偆丅
丂偝傜偵丄亅乮儅僀僫僗乯婰崋傪偳偆惗搆偼夝庍偟偰偄傞偐偲偄偆偙偲偱巜摫朄傕曄傢偭偰偒傑偡丅惗搆偑丄乥-a乥=a 偲摎偊傞側傜丄a 偑曄悢偱偁傞偙偲傪棟夝偝偣傞偙偲偲摨帪偵(亅)婰崋偑丄晧悢傪昞偡偺偱偼側偔丄儀僋僩儖揑偵晞崋傪曄偊傞摥偒傪偡傞婰崋偲擣幆偡傞偙偲傕昁梫偱偟傚偆丅愨懳抣偑濨枂側曄悢偺戝偒偝傪曪妵揑偵媮傔傞偺偵懳偟丄(亅)婰崋偼捈愙揑偵嶌梡偡傞栿偱偡丅偙偆偄偭偨弌敪揰偺堘偄偐傜傕愨懳抣偼嬯偄枴傢偄傪傕偭偰嬯偟傔偰偔傟傑偡丅
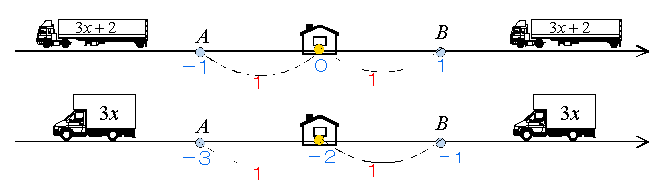
丂偝偰丄杮暥偺撪梕偱偡偑丄慜敿偺壠偲幵偲椫僑儉偼偦傟偧傟丄掕悢(掕揰)偲曄悢(摦揰)偲(亅)婰崋傪僷儘僨傿偭偰偄傑偡丅椫僑儉偺怢傃弅傒偱晄摍幃偺昞尰偟傛偆偲偟偨偺偱偡偑丄偪傚偭偲幐攕偩偭偨偐傕偟傟傑偣傫丅梀傃偡偓傞偲儘僋側偙偲偑偁傝傑偣傫丅
丂屻敿偼丄曄悢傪幵偱昞偟丄x丆2x丆2x+3 偲曄偊偰偄偔條傪幵偺戝偒偝偱椺偊偰偄傑偡丅嵍曽岦偐傜掕悢偲曄悢傪廍偭偰偄偒丄乽亙乿丄傗乽亝乿偱寢傋偽帺慠偲夝偑摼傜傟傑偡丅曄壔偡傞揰丄曄壔偟側偄揰傪偦傟偧傟壠偲幵偱抲偒姺偊傞偲悘暘偡傫側傝偲棟夝偑偱偒偨側偲姶偠傑偡丅
丂側偍丄杮暥偺悢捈慄忋偺帺摦幵偼偡傋偰嵍曽岦(x幉晧曽岦)傪岦偄偰偄傑偡丅懠堄偑偁偭偨傢偗偱偼偁傝傑偣傫丅帺摦幵偺僀儔僗僩偱塃岦偒偺偑庤尦偵側偐偭偨偩偗偺偙偲偱偡丅幵偺岦偄偰偄傞曽岦傕峫偊偰巜摫傪傾儗儞僕偟偰傕傜偊傟偽偲巚偄傑偡丅






 亂嵽丂椏亃丂杮帪偱巊梡偡傞慺嵽
亂嵽丂椏亃丂杮帪偱巊梡偡傞慺嵽 乻婎杮曇1乼丂丂乣僇乕僪偺抣偐傜愨懳抣傪儊僀僋傞
乻婎杮曇1乼丂丂乣僇乕僪偺抣偐傜愨懳抣傪儊僀僋傞