札幌藻岩高校 中村 文則


札幌藻岩高校 中村 文則

 【材 料】 本時で使用する素材
【材 料】 本時で使用する素材
【下ごしらえ】
 【調 理】
【調 理】
みんなの身近にある放物線ってなんだろうか?……分からない、じゃあヒントだ、放物線は「パラボラ」ともいう。この言葉から連想してごらん……、
そう、衛星アンテナのことだね。パラボラアンテナ。正確にはアンテナの表面が放物面になっていて、アンテナの軸に平行に切った切り口が放物線なんだ。ではなぜ衛星アンテナの表面が放物面かというと、放物線には電波や光を集める性質があるからなんだ。宇宙で分散してアンテナの軸に平行に入ってきた電波は、軸の先端にある集積器に集まり、家庭のテレビに送られる。この原理を逆に応用したのが懐中電灯で、豆電球で発光した光は放物面に当たり、軸に平行に反射するから照らすことができるようなる。この豆電球の部分を放物線の焦点という。
ところで、人間にも焦点があるけどどこだかわかるかな?……、こころだよ。人は心で相手の気持ちを受け止めるだろ。それが大事な人なら相手のすべてを受け入れたいと思うから、自然、体の形が放物線に近くなる。腕を上げ、そしてまげて、大事な人の気持ちを抱きしめるように相手の方に向かって伸ばすだろう。そして、受け入れた熱い気持ちを胸の奥にあるハート型の心に送っているわけだ。
さて、そこで今日は、体で放物線を表現することを試みて見よう。
《基本編1》 ~からだで放物線をメイクる(ボディパラ)
〇放物線準備体操
腕を空に向かってやや広げ気味に伸ばします。
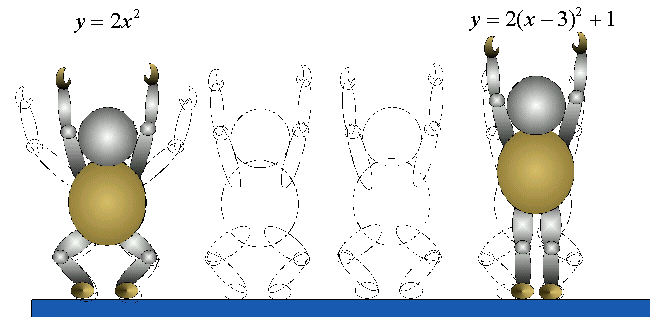
この形を基本形とします。すなわち、y=ax2 において、a=1 の場合です。
腕をゆっくりと上に上げ、狭めていきましょう。なお、掌は、内側に向くようにしましょう。この動作は a>1の場合を表現していることになります。その際、a=2,a=3 と喋りながら狭めていくと効果的です。腕が両耳にくっつくくらい狭まったら、基本形に戻してください。今度は、腕を徐々に広げていき、水平の位置になったら止めます。これは 0<a<1の場合で、水平の位置は a=0です。次に、一呼吸おいてから、上に向いている掌を反して下に向けます。そしてゆっくりと下に下げていき、a<0 の場合を表現していきます。
なお、放物線の意識付けを高める意味で胸にペンダントを掛けておくと効果的でしょう(もちろん、上に凸の場合は使えませんが)
さあ、一連の動きが終わったら、掛け声を掛けて放物線準備体操Go!。


オイッチ、ニー、サン。腕を高く挙げていこう。
次は、サン、ニー、オイッチ、ハン(ブン)、ゼロ、腕を広げて水平。
ゆっくり深呼吸して、掌を下に向けよう。
ゼロ、マイイー(-1)、マイニー(-2)、マイサン(-3)
下に向かって腕を下げ、両脇に近づける。
最後にゆっくりと基本形に戻して終わり
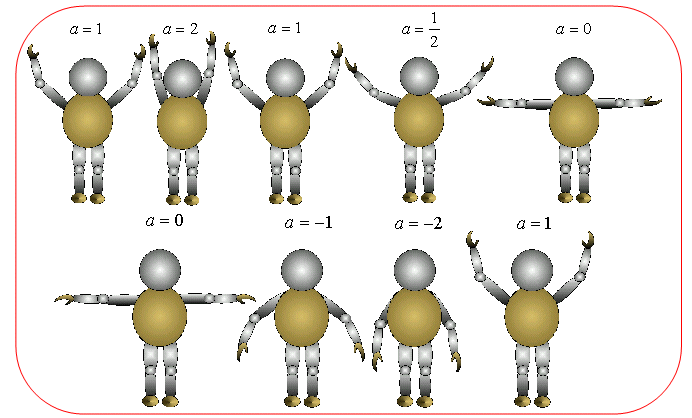
※留意事項《基本編2》 ~ボディパラたてよこ移動
最初はまず先生が見本をみせよう。先生がバカにならないと生徒もバカにはなれないもの。
〇上下方向の移動 (y=ax2+q のグラフ)
|
ex) y=2x2-1 のグラフを表現しよう。 ①黒板に大きく座標軸を描く。 ②基本形から手を揚げて、まず y=2x2のグラフ。 ③次にゆっくりしゃがんで y=2x2-1のグラフ。 |
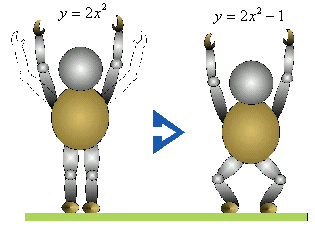 a,q の値をいろいろ変えて、生徒に上下運動をさせてみましょう。特に、q>0 のときは上の方向に飛ぶことになりますが、その地点できちんと静止するよう義務付けましょう。止まっていれない生徒に対しては厳しく指導します。
a,q の値をいろいろ変えて、生徒に上下運動をさせてみましょう。特に、q>0 のときは上の方向に飛ぶことになりますが、その地点できちんと静止するよう義務付けましょう。止まっていれない生徒に対しては厳しく指導します。|
ex) y=-2(x-3)2 のグラフを表現しよう。 ①基本形から腕をさげて、まず y=-2x2のグラフ。 ②右にゆっくり動いて y=-2(x-3)2のグラフ。 |
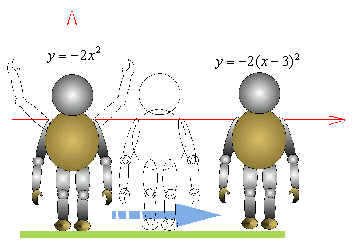 pの値を1,2,3と変化させて生徒を動かしてみましょう。ペンギン歩きに見えれば最高!。
pの値を1,2,3と変化させて生徒を動かしてみましょう。ペンギン歩きに見えれば最高!。基本形から標準形を踊って見ましょう。
| y=ax2 → y=a(x-p)2+q |
①まず先生が見本を見せる。標準形をいって、その形になるように実際に動く。(ガマン)
②生徒に標準形を言わせ、動いて見る。(ガマン、ガマン)
③今度は生徒に当てて、動いて貰おう。(さあ、やって貰おうじゃないか)
④他の生徒にどんな形になるか考えさせよう。
ex) 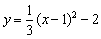 のグラフを踊ろう のグラフを踊ろう
|

《応用編1》 ~Let's dance BodyPara Para Para!
一般形から標準形を踊ってみましょう。
| y=ax2+bx+c → y=a(x-p)2+q |
①生徒に適当な一般形を言わせ、他の生徒に踊ってもらう。
②式変形ができず踊れない場合は、一般形をいった生徒に責任を持って変形させる。
③そして、レッツ!ダンス!
《応用編2》 ~最大・最小問題を解こう
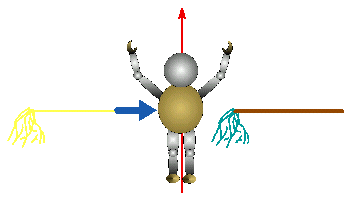 〇定義域が変化する最大・最小
〇定義域が変化する最大・最小
①生徒に標準形を躍らせる。
②掃除用具箱の中にあるモップを持って、左方向からゆっくりと生徒に近づける。
③モップを定義域に見立てて最小をとるx の値が変わった時点で生徒に「ストップ!」と声を掛けさせる。
④最大の場合も同様にする。
⑤ストップがかからない場合は、柄の先でちょっと突付いたり、頂点にあたる胸の部分を軽く柄で押して見よう。
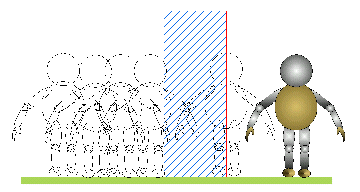 〇グラフが変化する最大・最小
〇グラフが変化する最大・最小
①黒板に定義域を描く。
②グラフの開きを固定し、生徒に黒板の右端からゆっくりと歩かせる。
③最小をとる xの値が変わった時点で生徒に「ストップ!」と声を掛けさせる。
④最大の場合も同様にする。
⑤ストップがかからない場合は、見ている生徒たちに掛けさせる。
《応用編3》 ~いろいろなグラフを踊ろう!
放物線の単元のみならず、いろいろな分野で曲線を体で表現してみましょう。
なお、掌の向きは、曲線が下に凸(掌を上)か上に凸(掌を下)かで区別します。
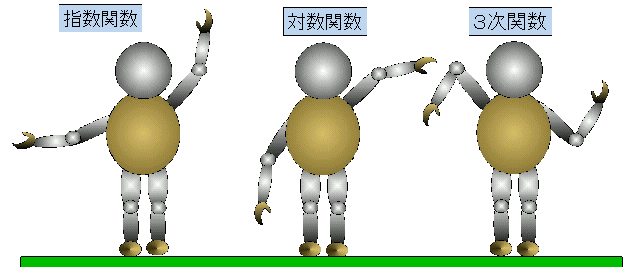
| 《指数関数》 |
教卓の板部分が漸近線になるようにしよう。 右腕と左腕の動き方に注意させよう。 y=ax のとき、a=1 を境に増加関数、減少関数が切り替わることに注目させよう。 |
| 《対数関数》 |
教室の壁(あるいは黒板の縁)を漸近線として使おう。 右腕と左腕の連動した動きに注意させよう。 |
| 《3次曲線》 |
変曲点でグラフが対称になるように腕の動きをつけよう。 最高次の係数でグラフが変わる様子に注目させよう。 |
あとがき
身近な素材を使うことがメイクる数学の真骨頂ですが、素材も使い尽くしてとうとうカラダに手を出すことになってしまいました。でも、カラダで放物線を形作ることはいろいろな面での発見を促します。
例えば視点の違い。放物線を俯瞰的に眺める立場と違って、放物線という乗り物(自分の体ですが)から周りを見ることには緊張感が伴ってきます。なぜならカラダは動いているわけですから制御するために思考と注意力が必要になってくるのです。同時に、仲間が放物線になって動いて姿を見ることは他の生徒にとっても特別な印象を持つことでしょう。一挙手一投足が新鮮に映っているはずです。
視点の違いは、最大・最小問題へのアプローチでは面白い現象を生み出します。放物線が動くことの方が自然になってしまいます。区間を横目に身体が通過する状態は放物線と区間が相対的な関係でしかないことを改めて教えてくれるでしょう。観ている生徒と実際に動いている生徒はまったく違った認識を持って問題に臨むことになるのです。
また、アナログ的動きを体感できることも利点です。どんなに放物線をコンピュータでシミュレートしようとそれはデジタルな動きでしかないのです。
しかし、基本形からグラフの開きを変化させて放物線準備体操をすると、a=-2,-1,0,1,2 を唱えながらも、その隙間の値を身体は埋めていっているのです。観ている生徒たちもまた放物線準備体操の動きから千手観音の流れような動きを見出すのではないでしょうか。
基本形から作り出される標準形の形も、単に変形の結果だけでなく、そこに人間としての「姿」も演出します。両手を挙げて背伸びする様はウルトラマンの飛び立とうとする姿でしょうか。両手をさげ、しゃがんで蛙。両手を広げて踏ん張って相撲の四股。慣れてくると身体を動かす生徒は標準形をいっただけでその姿を想像し、表情で顕します。それを見ている生徒たちも同時に顔を輝かすのです。
ところで、文中、ボディパラたて移動では、「ウルトラマンにはなれない」といって、y=2x2+1 のグラフをどう生徒は表現するかを問うています。何も条件をつけなければ生徒は手を上に伸ばした状態からジャンプして終わります。しかし、ここで「標準形の状態で停止すること」と条件をつけると生徒はどうするでしょうか。きっと聡明なあなたの生徒は少し考えてからこういうでしょう。
「先生、もう一度最初からやってもいいですか」
生徒は基本形の表現をするときに、しゃがんだ状態から始めます。そしてそのあとニコッと笑いながらすっくと立ちあがることでしょう。
この条件をつけた問いかけは実は重要な意味をもっています。標準形の形を姿として認識する一方、その位置を把握することも大切なことでしょう。しゃがんだ状態を基本形とみることで、生徒はx 軸を下方にさげたわけです。生徒がグラフを描くとき、y=(x-1)2+3 のようにx 軸上方に浮かんだグラフでは両座標軸は十字を切って作る必要はなありません。x軸の上方部分だけ描けば十分であり、x軸はずっと下方に書いて構わないことになります。しゃがんだことにより、グラフの位置によって見通しがいいように座標軸を設定することを生徒は学んだわけです。
そしてそのとき、生徒はウルトラマンになれるのです。