
札幌藻岩高校 中村文則
○はじめに
「ハノイの塔」は120年前に考案されたパズル玩具であり,いまでも広くパズル愛好家に親しまれている.それは有名パズルがみなそうであるように,その規則性のシンプルさと並べ替えの面白さに拠る.ルールは簡単.板の上の3本の棒の1つに突き刺された大小の円盤を他の棒に次の規則で移し換えるゲームである.
①1回に1枚の円盤しか移動できない
②移動した円盤はそれより大きな円盤の上に乗せる
③移動した円盤は3本の柱のいずれかに必ず差し込む
|
単純な規則だから,誰でも取り組め,実際にやりだすと手が止まらなくなるのだ.
このパズルに関しては「バラモンの塔」という次の逸話もよく知られている.
「インドのガンジス川ほとりの町ベナレスのバラモン教の寺院には,世界の中心を表すという聖堂がある.この聖堂の中には3本の大理石の柱が立っており,その1本には当初,大小64枚の黄金の円盤が,大きい円盤から順に重ねられていたという.この円盤をバラモン教の僧侶(ブラフマン)が昔から昼夜を問わず上記の規則で移し換えている.さて,バラモン教の教えでは,最初にこの円盤を1番目の柱に重ね並べたのは神であり,僧侶がすべての円盤を3番目の柱に移し換えたとき,この世は崩壊し終焉を迎えると言われている.
僧侶は今も滅びに向かってひたすら円盤を移しているのである.
このぞっとするある意味では崇高な伝説もこのパズルを解くことの興味を掻き立てるのである.
ところでわれわれはバラモン教の僧侶ではないから,はっきり言えば上記の規則なんかはどうでもいい.このパズルでもっと楽しく数学を遊べればと思う.そこでここでは日夜苦行を続ける僧侶を尻目にルールをちょっと改ざんして数列の教材とみてハノイの塔のパズルを考えてみよう.
なお,円盤の枚数はn枚とし,並べ方は最短の手数(てかず)を考えるものとする.
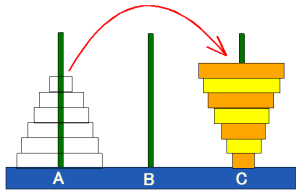
Ⅰ. Aの位置にある塔をCの位置に逆立
《移動のルール》
①1回に1枚の円盤しか移動できない
②移動した円盤は3本の柱のいずれかに必ず差し込む
|
逆立とは,小さい円盤から順に大きい円盤を積み重ねることをいう.これに対して正立はハノイの塔の通常の積み重ね方としよう.
さて,この場合は逆立させることより「円盤はそれより大きな円盤の上に乗せる」というハノイの塔の基本ルールは必要ない.したがい,ルールはないようなものであり,最短の手数 も容易に求められるだろう.もちろん小さい円盤から順番に1個ずつすべてを に移せばよい.
an=n
である.
Ⅱ. Aの位置にある塔をCの位置に正立

《移動のルール》
①1回に1枚の円盤しか移動できない
②移動した円盤は3本の柱のいずれかに必ず差し込む
|
塔全体をA→Bは逆立,B→Cは正立に移動させる.その手数はn+n=2nと勘違いされがちである.
ハノイの塔の円盤移動の目的は
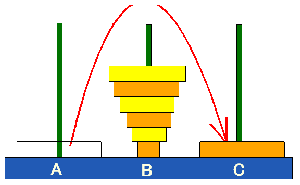 であることを注意したい.この場合,一番下になる円盤は最大サイズの円盤であるから,この円盤が自由に動くことができるように,他の円盤を別の棒に移していくのである.
であることを注意したい.この場合,一番下になる円盤は最大サイズの円盤であるから,この円盤が自由に動くことができるように,他の円盤を別の棒に移していくのである.
したがって,まずAの棒からBの棒へ上から順に(n-1)個の円盤を移動させる.そして一番最後のn番目の円盤を剥き出しにして,その円盤をCへ移動する.次に,Bの棒に差し込まれた逆立している(n-1)個の円盤をCに移していく.よって,その手数の総数anは,
an=(n-1)+1+(n-1)=2n-1
となり,単純に移動する場合より手数が1つ減る.
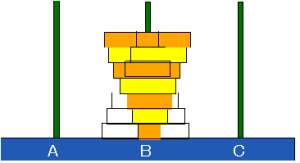
Ⅲ.Bの位置にある塔を同じ位置に逆立
《移動のルール》
①1回に1枚の円盤しか移動できない
②移動した円盤は3本の柱のいずれかに必ず差し込む
|
一番下にくるのは最小円盤であるから,基本原則によりこの円盤を最優先する.
まず,Bにある一番上の最小円盤をAに移し,Bにある残りの(n-1)個の円盤を順にCに逆立に移していく.次にAの最小円盤をBに移す.これで最小円盤が目的の位置に移された.
次にCに逆立している(n-1)個の一番下の円盤を優先する.残りの(n-2)個をAに正立に移していき,最後に一番下の1個をBに移す.
後は,Aにある(n-2)個の円盤をBに移して終わりである.
以上より,その手数は,
an=1+(n-1)+1+(n-2)+1+(n-2)=3n-2
である.
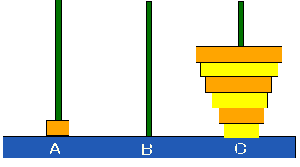
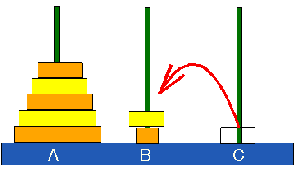
Ⅳ.Aの位置から他の位置に正立
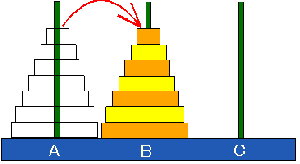
《移動のルール》
①1回に1枚の円盤しか移動できない
②移動した円盤は3本の柱のいずれかに必ず差し込む
③移動した円盤はそれより大きな円盤の上に乗せる
|
通常のハノイの塔のルールによる移動である.
このルールはアルゴリズムとして帰納法の問題とみることができる.
円盤の枚数を2,3,4,5,……と増やしていき,その手数anを予想してみるとよい.
a2=3,a3=7,a4=15 ぐらいは楽しんでいるうちにすぐに見つけられる.そのうち,
a2=a2-1,a3=23-1,a4=24-1
に気が付くだろうから,すぐにan=2n-1が予想される.あとはこの予想が正しいことを例えば数学的帰納法なんぞを使って示すことになる.ここでは「最下位円盤優先」の基本原則を元に説明しよう.
例えば,3枚の場合は,まず2枚を他の棒に移動させ,一番下の円盤を目的の棒に移す,最後に残りの2枚を移動させることになる.したがってその手数は,
a3=a2+1+a2=2a2+1=2・3+1=7
同様に,4枚の場合は,
a4=a3+1+a3=2a3+1=2・7+1=15
以下,続けていけばよい.これを2枚の場合から順次考えていけば,
a2=1
a3=1+2a2=1+2(2+1)=1+2+22
a4=1+2a3=1+2(2+1+22)=1+2+22+23
よって,
an=1+2+22+…+2n-1=(2n-1)/(2-1)=2n-1
となる。なお,an-1とanの関係をみると,
an=an-1+1+an-1=2an-1+1
これから数列{an+1}が公比2の等比数列になることから,
an+1=(a1+1)2n-1=2n
このように,ハノイの塔の移動は,漸化式の問題としてみることもできる.
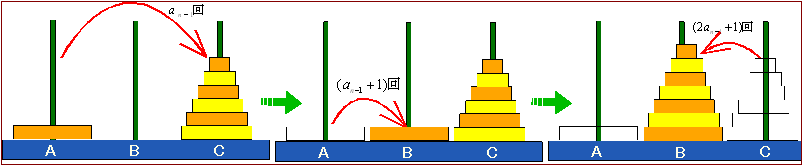
Ⅴ. Aの位置からCの位置に正立
バラモンの塔の逸話では,第3の棒に円盤を移し換えるとある.すなわち,移動する円盤は指定されており,残りの第2の円盤は補助棒的に使われている.では,最短の手数で指定した棒に移動するにはどうしたらいいだろう.
例えば2枚の場合,一番上の円盤をBに移すと,その下の円盤はCに移る.よって,2つの円盤はCに移ることになる.すなわち,一番上に置いた場所と違った場所に最終的に円盤はみな移る.
3枚の場合は,一番下を動かすためにはその前に上の2枚を動かすわけだから,その2枚の移動する棒は,一番上の円盤を置いた棒とは異なる棒である.したがって一番下の円盤は,一番上の円盤を最初に置いた棒に移ることになり,円盤全体は最初に置いた棒の位置にすべて移動する.
このように考えていくと,次の結論を得る.
Aにある塔を最短の手数anでCにすべて移すには,
円盤が奇数枚ある場合は,一番上にある円盤をCの棒に移す.
円盤が偶数枚ある場合は,一番上にある円盤をBの棒に移す.
|
ハノイの円盤の移動は,個数2個の移動を基本として,2個毎にその下の円盤を基本原則に基づき優先させ,移動させていく.しかし,実際に円盤の移動の操作をしてみると,人間の頭では,3個をブロックとして(7回の移動を)考えたほうが良さそうである.3個の移動は,一番上の円盤が移動した場所が3個のブロックの移動場所に一致し,全体の移動が見やすいのである.
ところで,バラモンの塔では,僧侶(ブラフマン)は昼夜黄金の円盤を他の棒に移す苦行を続けている.円盤の枚数は64枚であったから,最短の手数ですべての円盤をCに移し換え苦行を終えるには最初の一手はBに置かなければならない.僧侶が一番始めに震える手で1枚目の円盤を置いた場所がCであったとしたら,滅びを迎える最後の一手で僧侶は神の御心を知ることになるのかもしれない.

Ⅵ.Bの位置から両端に位置に偶数番目と奇数番目の円盤を分けて正立
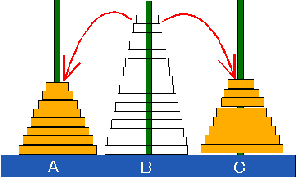
《移動のルール》
①1回に1枚の円盤しか移動できない
②移動した円盤は3本の柱のいずれかに必ず差し込む
③移動した円盤はそれより大きな円盤の上に乗せる
|
単純操作で考えれば,まず,Bにあるn個の円盤から最下位の円盤を除いた(n-1)個の円盤をAに移し,Bに残った円盤をCに移す.
次に,Aの上から(n-2)個をCに移し,今度はCの(n-3)個をAに移す.以下,交互に円盤の個数を1個ずつ減らしながらAとCの棒に振り分けていけば,最終的にはすべて両端に偶数番目と奇数番目の円盤に分けられる.
したがってその手数をbnとし,通常ルールのn個の円盤の場合の手数をanとすれば,
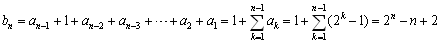
となる.
しかし,これが最短の手数でないことは明らかである.
例えば,b2=22-2+2=4となるが,実際には,Bの円盤を両端に振り分けるだけであるからb2=2である.
b3については,
Bの上の2枚をA⇒Bの一番下をC⇒Aの一番上をC
とすれば,b3=5でいいことになる.上述の振り分けより2手減っている.
実は上述の計算は,「最下位円盤の優位性」の捉え方に誤りがある.
円盤を中央の棒Bから両端の棒A(or C)に移す場合と,両端の棒から中央の棒に移す場合では,最下位円盤が異なるのである.この2つの場合について具体的にみてみよう.
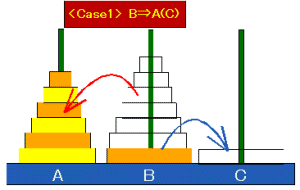
《Case 1》中央棒(B)⇒両端棒(A or C)
|
「最下位円盤の優位性」より, n個の円盤から最下位を除いた(n-1)個の円盤を両端のどちらかに移動し,最下位の円盤を残りの両端に移動する.
よって,この移動の回数は,通常n個のハノイの最小手数をanとすると,
an-1+1=(2n-1-1)+1=2n-1
となる。
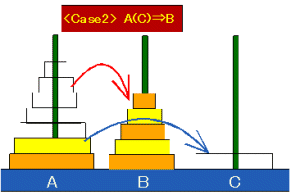
《Case 2》両端棒(A or C)⇒中央棒(B)
|
n個の円盤のうち,一番下にある最大サイズの円盤は両端に配置される円盤のひとつであるから,その上の円盤が移動対象となる最下位の円盤である.したがって,上から(n-2)個の円盤を中央棒Cに移し,(n-1)番目の円盤をもうひとつの端に移せばよい.よって,移動の回数bnは,
an-2+1=(2n-2-1)+1=2n+2
となる.
このようにCase2の手数はCase1の手数の半分でいいことがわかる.したがって中央棒に移す回数を最大限とるために,
C→A→B→C→B→A→B→C→B→A→…
のように,交互に両端と中央棒を移動させればよい.
このことから,n枚の円盤の最短手数bnを求めると,
b3=22+20=5
b4=23+21+20=11
b5=24+22+21=22
となる.さらに抜き出していくと,
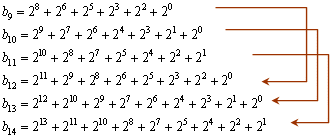
個数が3枚増える度に,同じ形の移動(アルゴリズム)が繰り返されることが分かる.このことから,最小手数bnは3を法とする剰余類で調べられる.
① n mod 3=0 のとき
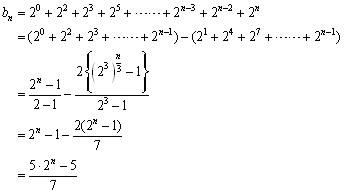
② n mod 3=1 のとき
bn=2bn-1+1である.ここで,n-1は3の倍数より,
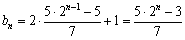
③ n mod 3=2 のとき
bn=2bn-1であるから,
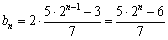
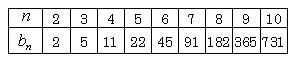 右表に具体的な手数を示したが,a10=1023であるから,通常のハノイの塔の手数に比べて意外と少ない結果となる.
右表に具体的な手数を示したが,a10=1023であるから,通常のハノイの塔の手数に比べて意外と少ない結果となる.
また,b9=365は,バラモンの塔伝説から考えても意味深な回数となっている.
○おわりに
パズル「ハノイの塔」は,フランスの数学者リュカ(Lucas)が考案したものです.リュカは,著書「数学遊戯」の中でクロー教授(Claus)に教えて貰ったと述べていますが,チャールズ・ドジソンがルイス・キャロルと名乗ったように,この数学家の洒落っ気たっぷりのアナグラム(文字の綴り換え)であることが後に判明しました.だから,もちろん「バラモンの塔」の伝説もリュカの創作であるということになります.
リュカはこの中で世界の終焉を64枚の円盤を移し終えることでリミットとしましたが,その回数は,最短の手数でも
264=18446744073709551615 (回)
と,トンデモない天文学的な回数となり,どうでもいい先の話となりますから,こんなところからもリュカの茶目っ気の一面を伺うことができます.
さて,本文ですが,その内容は読まれても分かりにくいところがあるかもしれません.ハノイの塔の醍醐味を味わうには実際に円盤を手で動かしてみるのが一番なのです.自分で円盤を操作してみると本文とは違った独自のアルゴリズムが見出せるかもしれません.
そのハノイの塔を作ることは簡単です.大小の消しゴミを用意し,縦に積み上げてもいいし,あるいは紙にピラミッド状に長方形を書いて切り抜き,平面的に並べてもいいでしょう(別紙に用意しました.よろしければご利用ください)
でもちゃんとパズルに腰を据えて取り組みたいのであればこの際,買ってしまいましょう.授業教材として売っているものは結構値の張る金額)が必要となりますが(レインボーハノイと商品名で3000円ぐらいだったような),玩具売場には安価で売っています.
この間,百円ショップで教材を物色していたら,なんと売っていました.「ダ○○―」というヒャッキンです.木製のもので,台座は縦20㎝,横8㎝,円盤は最大サイズ6㎝から最小サイズ2.5㎝まであって,これがなんと7個もついていますから,127回の手数が楽しめることになります.クラス人数分買ったって4200円,これだけの出費で新たに数学好きが増えること間違いなしです.
今回のレポートも実は傍らにその玩具をおいてアルゴリズムを確認しながら書き上げたものです.偶数番目,奇数番目の円盤を振り分ける最後の問題は,その玩具が茶色とクリーム色に塗り分けられていたことから,自然と浮かんできました.この問題を,棒の両端に配置された状態から中央に元の塔に復元するところから始めると,また違った見方が生まれます.
ところで,ハノイの塔は,いろいろなバリエーションで楽しみことが可能です.棒の数を4本にするとどうなるでしょう.その手数aは,a2=3,a3=5,a4=9,a5=13 であり通常ハノイと較べて随分回数は減ってきます.また,ハノイの塔の移動が自己相似形であることからその移動を音符に対応させ作曲したものをインターネットでみつけました.ネットでハノイの塔を検索すると凄い件数がヒットしてきます.隠れハノイファンがどれだけ多いか伺えます.きっと授業で40人が触りだしたら,40通りの新しいハノイ塔のアルゴリズムが見つかるかもしれません.
最後にハノイを授業で導入する際の引き込み方をひとつ.
「この右端に積み上げられた円盤を,左端に移すにはどうしたらいいだろう」
ちょっと,生徒に間かさせてから,
「こうやるんだ」
といって,中央棒を持ち,台座をクルッと 回転させます.
「ずるい,先生」…ワイワイガヤガヤ……ここから,ルールが始まります.
※各紙片を切り取って,平面ハノイとしてお楽しみください.




 であることを注意したい.この場合,一番下になる円盤は最大サイズの円盤であるから,この円盤が自由に動くことができるように,他の円盤を別の棒に移していくのである.
であることを注意したい.この場合,一番下になる円盤は最大サイズの円盤であるから,この円盤が自由に動くことができるように,他の円盤を別の棒に移していくのである.






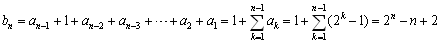


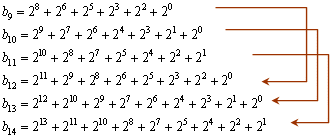
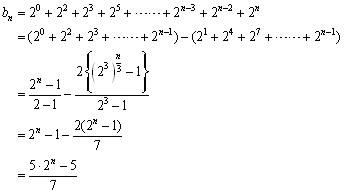
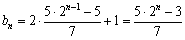
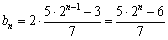
 右表に具体的な手数を示したが,a10=1023であるから,通常のハノイの塔の手数に比べて意外と少ない結果となる.
右表に具体的な手数を示したが,a10=1023であるから,通常のハノイの塔の手数に比べて意外と少ない結果となる.