ｅｘ1) 分数関数 の逆関数を求めよ。

　どうってことのない問題かもしれない。旧数�Tから、現教育課程では数�Vへとこの分野は移されしまったが、逆関数を説明するには、分数関数（双曲線）ほどの好例はない（応用として指数・対数関数が続くが）だろう。

　ところで、教科書では、逆関数の定義からその具体的な求め方を次のように説明する。

�@ 式ｙ＝ｆ(ｘ)からｘ＝ｇ(ｙ)の形の式を求める。 �A ｘとｙを入れ替えて、ｙ=ｇ(ｘ)の形にする。

　こうして実際に逆関数を求め、その後に逆関数のグラフ上の性質について触れていく。

関数 ｙ＝ｆ(ｘ)のグラフとその逆関数 ｙ=ｆ−１(ｘ) のグラフは、直線ｙ＝ｘに関して対称である。

　このように性質を視覚的にも理解させていくのが一般的な指導の流れなのであろう。

　さて問題はこの後である。演習で再び上述の逆関数を求める問題がでると、ｘについて解きｘとｙを入れ替える…となってしまう。せっかくイメージとして捉えていた性質が、「計算技術」の方に傾き忘れ去られてしまう。

　曲線の概形が関数から判断しにくいのであれば、この方法は止むおえないのであろうが、双曲線のグラフは、漸近線および原点(中心)とグラフとの離れ（焦点の位置）の２つの要素で決定するわけだから、これを利用して逆関数のグラフ的な位置関係から説明できるはずなのである。このことについて、以下、考察してみよう。

　双曲線の方程式の一般形からはグラフの性質を読取り難いから、標準形へと変形する。

（一般形） ⇒ （標準形） ……�@

　これから関数は、（基本形）のグラフをｘ軸，ｙ軸の正の方向へそれぞれｐ，ｑだけ平行移動したものである。このときｘ＝ｐ，ｙ＝ｑが漸近線となる。ここで、のグラフは、直線ｙ＝ｘに関して対称なグラフであるから逆関数もである。逆関数の漸近線はｘ＝ｑ，ｙ＝ｐより、その方程式は、 となる。

　したがって、�@の変形ができれば逆関数は求められることになる。

《双曲線の一般形から標準形への変形》 と変形でき、漸近線は、 　ここでｋの値は、に（漸近線）を代入したものである。

　

解説)　 の分母を払う。
　　　　
　これをｘの恒等式とみて を代入すると　 である。

　よって、次の結果を得る。

《双曲線の逆関数の求め方》 の逆関数は

　これから、ｅｘ1)の解答は次のようにまとめられる。

解)　　　　<ｋ＝3(-2)+4=-2>
　　より逆関数は、　

　このように考えるとグラフの概形もつかめ、問題への応用も広がっていくことになる。例を挙げると、

【問１】 関数 とその逆関数が一致するときａの値を求めよ。

　解) 漸近線はｘ＝−2，ｙ＝ａより、逆関数の漸近線はｘ−ａ，ｙ＝−2 ∴ａ=−2

【問２】分数関数 が次の条件�@，�Aを満たすとき、ｆ(ｘ)を求めよ。
　�@　ｙ＝ｆ(ｘ)とその逆関数は一致する。
　�A　ｙ＝ｆ(ｘ)は直線ｘ＝１を漸近線として、点(２,３)を通る。

　解) とおける。 ｆ(2)＝3 よりｋ＝2 ∴

　しかし、前述の方法ではｋの値が分数になると計算が面倒になり、結果はまた計算力に頼る形になってしまうことがある。たとえば、

ｅｘ2) 分数関数　の逆関数を求めよ。

　解) 漸近線は。を分子に代入してｋを得る。
　 ∴
　よって、逆関数は、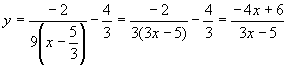

　このように非常に煩雑な計算することとなり、これなら機械的に解いた方がよいだろう。そこで、次のように考え方を発展させてみよう。

《双曲線の逆関数の求め方２》 分数関数 に対して、 である。

　この証明は分数関数をｘについて解いてからｘとｙを入れ替えるともちろん簡単にできるがそれでは意味がない。

　関数ではなく曲線とみて考えてみよう。

　　ｙ＝ｆ(ｘ)の漸近線は、より とおける。
　ここで より、は上の点。
　代入して（分子）＝０よりｋ_１＝ｂとなる。

　このようにグラフ上の性質を追うと、中心からの遠さを表すｋの代わりに曲線上の点を要素として使えば逆関数を求めることが可能となる。

　よって、ｅｘ２)の逆関数は、 とおけるから、
　　　より　ｋ＝6　∴　となる。

　Ｎｏｔｅ）

　　行列を使って次のように考えても面白い。

　　分数関数の分子・分母の係数を行列の成分とみると、
　　 　　 ⇒
　と対応させることができる。ただ、この対応は、一意的ではない。
　　　だから、となる。

　しかし、この行列で変換してからまた分数関数に対応させれば分子、分母で約分できるから支障はない。次に、
　　　　ｙ＝ｆ⁻¹(ｘ) ⇒
と対応できることから、逆行列により逆関数がきまる。例を示そう。

【問３】のとき、ｙ＝ｆ⁻¹(ｘ)を求めよ。

　解) 行列　 に対応させる。 より、
　　　　
　さらに、この考え方は合成関数にも応用ができる。

【問４】 のとき、次の関数を求めよ。
　　　(1)　(2)

　　解)(1) ⇒
　　　 (2) ⇒

　このようにずいぶん計算はラクになる。ただ、この方法は高校生レベルでは行列との対応が理解しにくく結局は、「安易でお得な方法」となってしまう危険性はあろう。

　まとめとして……

　双曲線の一般形から標準形への変形をすんなりとできる生徒が意外と少ないのにいつも驚かされる。分数式での計算演習が不十分といってしまえばそれまでだが、どうも式の意味が理解できていないようでもある。
　　　　 ………(*)
　ここらあたりの関係が曖昧なのである。もっともこういう変形は妙ではある。左辺は、分数(式)を、右辺は割算を表すわけだから普通は、割算した計算結果が分数とならなければならないから計算過程が逆である。しかし、分数式は、割算の内容をまとめたことを意味する場合もあるのである。ところで数においては割算の計算結果は、商と余りを求めることである。分数式でももちろんこれは同様であるが、分数式自体の存在感がずいぶん大きいためか計算をしにくく感じてしまうようだ。(*)を実際に割ると、
　　　　
となり、商と余りが求められる。

　　　　とおくと、…�@
　　∴　
　よって、双曲線の一般形から標準形への変形は、商と余りを求めることであり、商ｑから漸近線ｙ＝ｑが得られると考えてよい。これを「分数式を変形して」などと生徒に要求すると、どう変形していいか分からなくなるのである。割算であることを理解させればけっして難しいことではない。この理解を前提として、
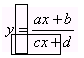　　　の漸近線は、　（極限で説明できればもっといいが）　　　　　　　　　　

　ｋの値は、�@より剰余の定理から求めればよいとすれば、単なる暗記にはならないのだろう。細かいことかもしれないが、「数学を知っている教師側」からは重要な当たり前のことがときどき省略されてしまうことがある。そこで生徒がつまずくと、教師も生徒も理由が分からないままに悩んでしまう。だから（白雪姫の魔法使いではないが）いつも鏡である生徒に問いかけることを忘れてはならないだろう。

　　　　　あなたはなにを知りたいの。そしてなにを知らないの。