 無理数である
無理数である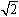 の値は近似式で求められます。あるいは手元に電卓があるのなら、ちょっと
の値は近似式で求められます。あるいは手元に電卓があるのなら、ちょっと キーを叩いてみれば済むことです。ただ、近似式は小数第何位かで狂いが生じ、また電卓はディスプレイの表示桁数に限界があります。
キーを叩いてみれば済むことです。ただ、近似式は小数第何位かで狂いが生じ、また電卓はディスプレイの表示桁数に限界があります。しかし開平法(平方根を求める方法)では、
 に限りなく近い値を求めることが可能なのです。
に限りなく近い値を求めることが可能なのです。
 無理数である
無理数である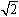 の値は近似式で求められます。あるいは手元に電卓があるのなら、ちょっと
の値は近似式で求められます。あるいは手元に電卓があるのなら、ちょっと キーを叩いてみれば済むことです。ただ、近似式は小数第何位かで狂いが生じ、また電卓はディスプレイの表示桁数に限界があります。
キーを叩いてみれば済むことです。ただ、近似式は小数第何位かで狂いが生じ、また電卓はディスプレイの表示桁数に限界があります。
しかし開平法(平方根を求める方法)では、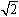 に限りなく近い値を求めることが可能なのです。
に限りなく近い値を求めることが可能なのです。
例 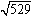 を開平してみましょう。
を開平してみましょう。
529=(10a+b)2=100a2+20ab+b2
とみると、102<529<104ですから、529は2桁の数です。そこで一の位が0である2桁の数の平方で529に一番近い数を求めると、20が得られます。次に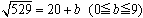 とおき、両辺を平方します。529=400+40b+b2よりb=3が分かり
とおき、両辺を平方します。529=400+40b+b2よりb=3が分かり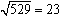 となり開平できました。
となり開平できました。
問 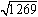 を開平してください。
を開平してください。
では、この計算の仕組みを考えてみましょう。
2桁の整数xは、x=10a+b(1≦a≦9,0≦b≦9)と表せます。
x2=100a2+20ab+b2
より、
x2-(10a)2=(20a+b)b
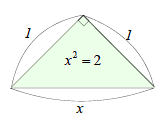
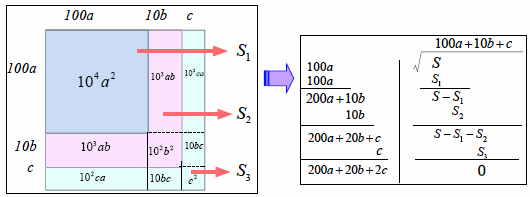
これは、図のようにx2を面積とみると、おおざっぱに十の位の数の平方を表す面積100a2を求めて、残りの面積から1の位の数を算出していることが分かります。
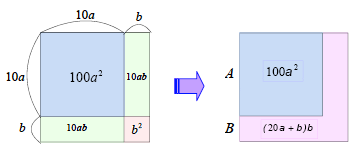
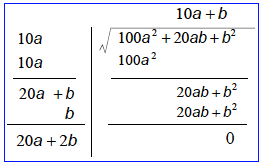 この計算を簡略化すると次のようになります。
この計算を簡略化すると次のようになります。
計算は2つのブロックに分かれています。左側は平方根の各位の数を求めている部分であり、右側は平方数の表している面積と、残りの面積を計算する部分です。
例 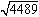 の開平で実際の計算の流れをみてみましょう。
の開平で実際の計算の流れをみてみましょう。
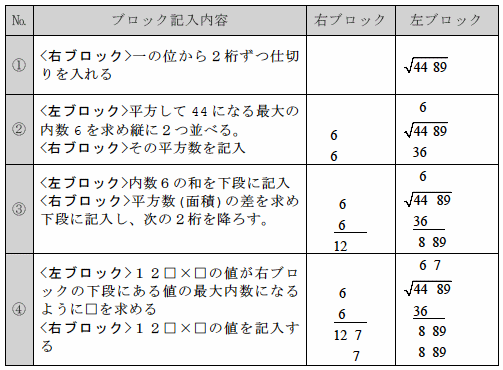
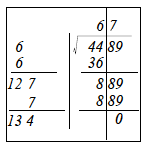 以下同様に計算し、右ブロックの面積の差が0になる(開ききる)まで続けます。
以下同様に計算し、右ブロックの面積の差が0になる(開ききる)まで続けます。
問 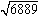 を開平してください。
を開平してください。
問 開平した値が3桁の場合でも同様の計算ができることを図で確認し、次の数を開平してください。
(1)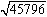 (2)
(2)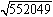
例 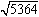 を開平してみましょう。
を開平してみましょう。
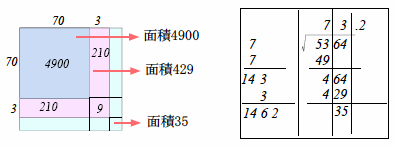
右がその計算結果ですが、面積が残ってしまいました(この面積を開平の残りといいます)。これは、
5634=732+35
となることを意味します。
そこで、さらに同様の手順で計算すると次のようになります。
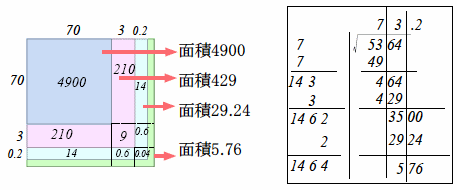
5634=73.22+5.76
となり、小数第1位まで平方根が開かれました。このように、開平計算では、おおざっぱに102の幅で平方数の表す面積を近似することによって、百の位、十の位、一の位、小数点第1位と値を絞っていくことができます。
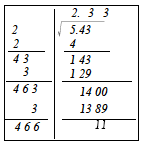 例
例 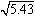 を小数第2位まで計算してみよう。
を小数第2位まで計算してみよう。
問 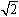 を小数第6位まで計算してください。
を小数第6位まで計算してください。
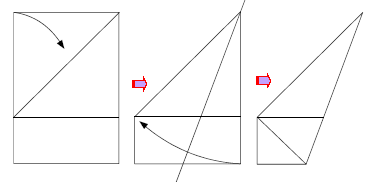
→西洋紙を半分に折ると、元の西洋紙と同じ形(相似)になります。そのためには西洋紙の2辺の比はどうなっていればいいでしょうか。