○ちょっとした誤手技？

＜先　生＞ 絶対値の記号｜｜は数から負符号をチェックし，奪い取る関所みたいなものですが，数直線上で点をプロットし，数学言語としてとらえれば，
　　　｜x−a｜⇔点A(a)から点P(x)までの距離
と翻訳できたんだったよね。この考えを利用して，絶対値のついた1次不等式を解いてみよう。

ex) 次の不等式を解け。 (1)｜x−3｜＜4　　　(2) ｜2x−3｜＜5　　　(3) ｜3x＋4｜＞2

＜先　生＞まず(1)だけど，そのまま日本語として読むと，「点3からxまでの距離が4より短い」となる。例えば，先生の今立っている場所を点3としよう。この点から4までの距離の点は左右2箇所あるけど，黒板に向かって右の場所はというと，……先生，1歩，2歩，3歩，4歩と右に歩き出す……この点だ。では，この点は何だ，まなぶ。

＜まなぶ＞…指折り4，5，6，7と数えて…はい，7です。

＜先　生＞今度は，左方向だ。……再び点3の位置に戻って歩き出す……，さあ，この点は，かず子。

＜かず子＞3−4＝−1です。

＜先　生＞従って，4より短い距離は，−1と7の間だから，その範囲の適当な数xに対して，−1＜x＜7となる訳だ。それでは，同様に(2)を皆で話し合って求めてごらん。

＜かず子＞まず，xの１次の項の係数が1でなければ直訳できないから，両辺を2で割って，
　　　
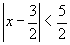
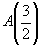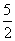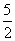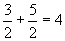　これから，点から点P(x)までの距離がより短いということですから，点aから右方向に進んだ点　　と，点aから左方向に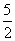進んだ点　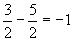　の間の範囲より，
　　　−1＜x＜4
となるわ。

＜よしお＞俺は，t＝2xと置きかえるな。すると点a(3)から点P(t)までの距離が5より短いという意味だから
　　　3−5＜2x＜3＋5
　よって，両辺を2で割って，−1＜x＜4となる。

＜まなぶ＞そうやって置きかえるならいっそのこと，まるごとt＝2x−3と置き換えてしまった方がラクだと思うな。
　　　−5＜x＜5　から　−5＜2x−3＜5
　これから，両辺に3を加えて2で割ればいい。

＜先　生＞どの考え方も面白いけど，今回は「まなぶ法」を採用してみようか。まなぶ法は，絶対値のとる値を一つの点とみて，原点からの距離と考える方法だね。
　　　｜P｜＜k　(0＜k)　⇔　−k＜P＜k
ということだ。では，まなぶ法で，(3)に挑戦だ。

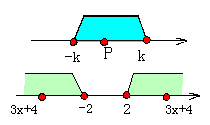
＜まなぶ＞原点から点P(3x＋4)までの距離が，2より長いんだから，
　　　3x＋4＜-2，2＜3x＋4
となるから，
　　　
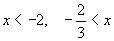
です。

＜先　生＞まなぶ法全開だな。では，次の問題に応用してみよう。

ex) 次の不等式を解け。 (1)　｜2x−3｜≦x＋1　　　(2)｜3x−1｜＞x＋3　　　(3)｜x−1｜≧2x＋3

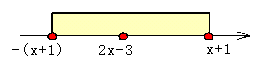＜よしお＞(1)を解きます。原点から点P(2x−3)までの距離がx＋1より短いから……

＜先　生＞不等号の部分に注意！。

＜よしお＞あっ，はい，短いか，等しいから
　　　−(x＋1)≦2x−3≦x＋1
です。左辺と中辺から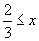，，中辺と右辺から，x≦4。共通範囲を求めて，
　　　
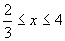
となります。

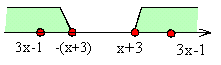＜かず子＞(2)も同じです。原点から点P(3x−1)までの距離がx＋3より長いわけですから，
　　　3x−1＜−(x＋3)，　x＋3＜3x−1
それぞれを解いて，
　　　
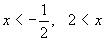
となります。

＜先　生＞では最後の問題はまなぶ法に敬意をはらって，まなぶに解いてもらおう。

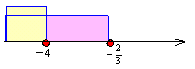＜まなぶ＞カンタンです。原点から点P(x−1)までの距離が2x＋3より長いか等しいんだから，
　　　x−1≦−(2x＋3)，　2x＋3＜x−1
それぞれを解いて，
　　　
で終わりです。

＜先　生＞本当に終わりかい。求めた解はまとめられないかな。

＜まなぶ＞えっ？。あっ。共通範囲を求めて，x≦−4です。

＜先　生＞ほんとう？。もともとの解は，図をみると2つの領域で与えられていたね。その場合は共通部分を求めるのかな。

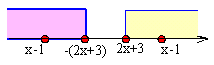＜まなぶ＞そうか。解を合わせるんだ。だから，
　　　
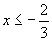
です。
　だけど，先生，全然，俺に敬意払ってないと思うんだけど！。

Ｎｏtｅ）

　　　このまなぶ法はどこまで，認められるでしょうか。