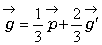嶥杫怴愳崅摍妛峑丂丂拞懞丂暥懃
廳怱偭偰側偵丠
亙愭丂惗亜崱擔偼偪傚偭偲嫵壢彂偲偼棧傟偨榖戣偵偮偄偰峫偊偰傒傛偆丅傒傫側偼傕偪傠傫廳怱偲偄偆尵梩偼抦偭偰傞偹丅亙傑側傇亜
偼偄丅拞妛峑偱廗偄傑偟偨丅 亙偐偢巕亜
亙偐偢巕亜
崅峑偵擖偭偰偐傜傕丄乽恾宍偲曽掱幃乿傗乽儀僋僩儖乿偺暘栰偵偱偰偒偨傢丅亙愭丂惗亜
偱偼丄偦偺廳怱偲偼偄偭偨偄側傫偺偙偲偩傠偆偐丅亙傑側傇亜
偦偆傑偲傕偵栤傢傟傞偲摎偊偵偔偄偗偳丄懡暘恾宍偑掁傝崌偆揰偩偲巚偄傑偡偗偳丅亙傛偟偍亜
嶰妏宍偺廳怱傪峫偊偨偲偒丄妋偐廳怱偵巜傪揧偊偰嶰妏宍傪忔偣傞偲僶儔儞僗偑庢傟傞偲偐廗偭偨偲巚偆丅亙偐偢巕亜
拞妛偺偲偒丄愭惗偑嶰妏宍偺廳怱偵捾梜巬傪巋偟偰嬵偺傛偆偵夢偟偰偔傟偨偺丅偔傞偔傞偲夞偭偰姶寖偟偨傢丅亙愭丂惗亜
廳怱偲偄偆尵梩偼偩偹丅偐偺傾儖僉儊僨僗偑乽廳椡偺曽岦偵掁傝崌偆揰乿偲偄偆堄枴偱柦柤偟偨傫偩丅恖娫偱尵偊偽傊偦傒偨偄側傕偺偩丅恾宍傪巺偵寢傫偱傇傜壓偘傞偲丄偦偺巺(偡側傢偪廳椡)偺墑挿忋偵廳怱偑忔偭偰偄傞偙偲偑暘偐傞丅偙偺偙偲傪棙梡偡傞偲幚尡偵傛傝娙扨偵廳怱偺埵抲偼扵偡偙偲偑壜擻偵側傞丅傒傫側偼傕偭偲傕僔儞僾儖側恾宍偱偁傞嶰妏宍偱偦偺廳怱傪妛傫偩傢偗偩偗偳丄偲偙傠偱丄偦偺嶰妏宍帺懱偼傒傫側偑拞妛偱廗偭偨傕偺偲崅峑偱廗偭偨傕偺偼摨偠恾宍傪昞偟偰偄傞偺偩傠偆偐丅亙傛偟偍亜
乧乧乧丄偄偭偰傞堄枴偑傛偔傢偐傜側偄偺偱偡偑丅亙傑側傇亜
摨偠偠傖側偄傫偱偡偐丅亙愭丂惗亜
懠偺恾宍偱峫偊偰傒傛偆丅椺偊偽墌丅偦偺曽掱幃偼偳偆昞尰偝傟偨偩傠偆丅亙傛偟偍亜
偼偄丄尨揰傪拞怱偲偡傞墌側傜 倶2亄倷2亖倰2 偲側傝傑偡丅亙愭丂惗亜
偱偼婳愓偲偟偰昞尰偡傞偲偳偆側傞丅亙偐偢巕亜
掕揰偐傜摍嫍棧偵偁傞揰偺婳愓偱偡丅亙愭丂惗亜
崱偺傒傫側偺擣幆偼偦偆側偭偰傞偹丅偱偼傒傫側偑弶傔偰墌偵偮偄偰廗偭偨偲偒偺婰壇傪屇傃婲偙偟偰偛傜傫丅弮恀偩偭偨偙傠偺彫妛惗偵娨偭偰傒傛偆丅亙傑側傇亜
偊乕偲丄扴擟偺愭惗偑丄乽墌偭偰偄偆偺偼偍寧條傒偨偄偵傑偁傞偄宍偩傛乿偭偰偄偭偰夋梡巻傪愗傝敳偄偰乧乧丄偁傟両丄拞恎偑側偔側偭偰偄傞丅亙愭丂惗亜
偦偺捠傝丅崅峑偱廗偭偨墌偺掕媊偼幚偼墌偺旂丄偡側傢偪墌廃傪昞偟偰偄傞丅壗屘偐偄偮偺傑偵偐媗傑偭偰偄偨拞恎偑側偔側偭偰偄傞傫偩丅摨條偺偙偲偑媴偱傕偄偊傞偩傠偆丅媴柺偑媴偲偄偆尵梩偵偡傝偐傢偭偰偄傞丅偳偪傜傕丄傕偲傕偲偺掕媊偱偼曽掱幃偼丄倶2亄倷2亝倰2 傗丄倶2亄倷2亄倸2亝倰2 偱偁偭偨偼偢側偺偩丅摨偠傛偆偵傒傞偲嶰妏宍偵偮偄偰偼偳偆偩傠偆丅亙偐偢巕亜
戙悢揑偵偼乽嶰妏宍偺撪晹偺揰乿側傫偰昞尰偑偱偰偒傑偡偐傜丄偙傟傕廃偩偗傪昞偟偰偄傞偲巚偄傑偡丅亙傑側傇亜
偱傕丄嶰妏斾偺偲偙傠偱偼丄乽嶰妏宍偺撪晹偺柺愊乿側傫偰尵傢側偄傛丅偩偐傜偙偺応崌偼拞恎偑媗傑偭偰偄傞偲巚偆側丅偦偆偡傞偲偳偭偪側傫偩傠偆偐丅亙傛偟偍亜
偆乕傫丅壗偐偦傟偧傟偺暘栰偱搒崌偺偄偄傛偆偵巊偄暘偗偰偄傞傫偱偼側偄偱偟傚偆偐丅 亙愭丂惗亜
亙愭丂惗亜
偦傟偧傟偺暘栰偭偰偳偆偄偆偙偲偩傠偆丅亙傛偟偍亜
偼偄丄戙悢揑暘栰偑廃偩偗偱丄婔壗揑暘栰偱偼撪晹傪娷傔偰偄傞偲偄偆偙偲偱偡丅亙傑側傇亜
偦偆偄偊偽丄墌偵偮偄偰傕婔壗偱偼丄廃偍傛傃撪晹偺柺愊傪丄扨偵墌偺柺愊偭偰偄偭偰傞丅亙愭丂惗亜
戝嶨攃偵傒傞偲偦傫側姶偠偩偹丅偱傕杮戣偼偙傟偐傜側傫偩丅偱偼丄嶰妏宍偺廳怱偼拞恎偺偁傞嶰妏宍偱峫偊偰偄傞偺偩傠偆偐丅偦傟偲傕廃偩偗偺嶰妏宍側偺偐偳偪傜側傫偩傠偆丅亙傑側傇亜
偆乕傫乧乧丄杔偼拞恎偺媗傑偭偰偄傞曽偩偲巚偄傑偡丅廳怱偲偄偆偺偼嶰妏宍偑掁傝崌偆揰側傫偩偐傜丅拞恎偑側偐偭偨傜掁傝崌偆偲偙傠偼嬻偺忬懺偵側偭偰偟傑偆丅亙傛偟偍亜
偱傕丄儀僋僩儖傗恾宍偺曽掱幃偱媮傔偰偄傞廳怱偼拞恎偺側偄嶰妏宍偱偼側偄傫偩傠偆偐丅亙偐偢巕亜
偩偲偟偨傜丄拞恎偑偁傞嶰妏宍傕偦偆偱側偄嶰妏宍傕摨偠埵抲偵廳怱偑偁傞偭偰偙偲偵側傞傢傛丅廳怱偺埵抲偼偳偪傜偱峫偊偰傕拞慄傪俀丗侾偺斾偵撪暘偡傞揰偱偟傚丅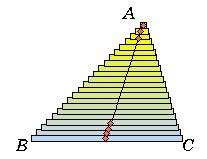 亙傛偟偍亜
亙傛偟偍亜
偱傕偦傟偼拞慄偺岎揰偑廳怱偲偄偆偙偲偐傜埵抲儀僋僩儖傪媮傔偨傢偗偩偐傜堦抳偡傞偺偼摉偨傝慜偩傛偹丅偲偄偆偙偲偼廳怱偺掕媊偦偺傕偺偵媈栤偑偱偰偔傞丅亙愭丂惗亜
偦傟偱偼惍棟偡傞堄枴偱丄傕偆堦搙嶰妏宍偺廳怱偵偮偄偰偍偝傜偄偟偰傒傛偆偐丅傑偢丄拞恎偺偁傞嶰妏宍偺応崌偩丅嬒幙偵敄偄斅忬偺嶰妏宍傪峫偊偰傒傟偽偄偄丅妋擣偡傞偗偳拞恎偑偁偭偰傕側偔偰傕廳怱偼嶰妏宍偑掁傝崌偆揰偱偁傞偲偄偆偙偲偩丅敄偄斅偱嶌傜傟偨嶰妏宍偼丄偐偢巕偺拞妛峑偺愭惗偑僐儅傪傑傢偟偰幚墘偟偰偔傟偨傛偆偵柧傜偐偵拞慄偺岎揰偑廳怱偵側偭偰偄傞丅偙偺偙偲偼嶰妏宍傪偁傞曈偵暯峴偵僗儔僀僗偟偰偄偗偽愢柧偑偮偔丅
椺偊偽恾偺傛偆偵曈BC偵暯峴偵嵶偐偔僗儔僀僗偡傞偲丄僗儔僀僗偝傟偨恾宍偼慄暘偵嬤偄挿曽宍偲傒傞偙偲偑偱偒傞丅偱偼偦偺偍偺偍偺偺挿曽宍偺廳怱偼偳偙偵偁傞偩傠偆丅
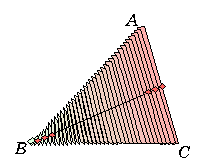 亙傑側傇亜娙扨偱偡丅偦偺挿曽宍偺恀拞丄偡側傢偪拞揰偵偁傝傑偡丅
亙傑側傇亜娙扨偱偡丅偦偺挿曽宍偺恀拞丄偡側傢偪拞揰偵偁傝傑偡丅亙愭丂惗亜
偦偺捠傝丅偙傟偼拞揰偵挿曽宍偺廳傒偑廤傑偭偰偄傞偙偲傪堄枴偟偰偄傞丅偦偟偰偙偺拞揰傪廤傔偨傕偺偑拞慄偵側傞偙偲偼暘偐傞偹丅偟偨偑偭偰丄嶰妏宍偺廳怱偼偙偺拞慄忋偵摉慠忔偭偐偭偰偔傞傢偗偩丅摨條偵崱搙偼曈CA偵暯峴偵僗儔僀僗偡傞偲傗偼傝拞慄偑晜偐傃忋偑偭偰偔傞丅埲忋傛傝偙偺俀偮偺拞慄忋偺岎揰偑廳怱偲側傞丅偱偼丄廳怱偑拞慄傪俀丗侾偺斾偵暘偗傞偙偲傪嶰妏宍偺掁傝崌偄傪傒傞偙偲偱帵偟偰傒傛偆丅掁傝崌偆偨傔偵偼廳偝偑昁梫偩偗傟偳丄偲偙傠偱嶰妏宍偺廳偝偭偰側傫偩傠偆丅嶰妏宍偑嬒幙側敄斅偱嶌傜傟偰偄傞偙偲偐傜峫偊偰偛傜傫丅
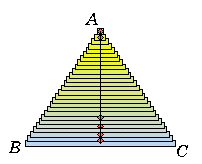 亙傛偟偍亜柺愊傪峫偊傟偽偄偄偲巚偄傑偡丅嶰妏宍偺懱愊偼柺愊偵岤偝傪偐偗偨傕偺偱偡偐傜丅
亙傛偟偍亜柺愊傪峫偊傟偽偄偄偲巚偄傑偡丅嶰妏宍偺懱愊偼柺愊偵岤偝傪偐偗偨傕偺偱偡偐傜丅亙偐偢巕亜
柺愊偼廳偝偵斾椺偡傞偲偄偆偙偲偹丅亙愭丂惗亜
偄偄昞尰偩偹丅偝偰愭傎偳曈BC偵暯峴偵僗儔僀僗偝傟偨忬懺偺嶰妏宍偺宍傪偪傚偭偲惍偊偰傒傛偆丅偦傟偧傟偺挿曽宍偺拞揰偑掙曈BC偺悅捈擇摍暘慄忋偵偔傞傛偆偵壛岺偟丄擇摍曈嶰妏宍傪嶌傞傫偩丅
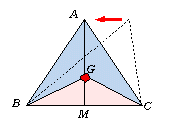
丂偝偰丄偄傑廳怱G偵傛傝仮ABC偼俁偮偺嶰妏宍丄仮GAB丆仮GBC丆仮GCA偵暘偗傜傟傞偑丄廳怱偱廳偝偑掁傝崌偆偲偒丄偙偺俁偮偺嶰妏宍偺柺愊偼傒側摍偟偔側傞偼偢偩丅曈BC傪掙曈偲偡傞仮ABC丆仮GBC偺崅偝傪峫偊傞偲掙曈偺挿偝偼嫟捠偱偁傞偐傜偦傟偧傟偺柺愊偼崅偝偵斾椺偡傞丅偟偨偑偭偰丄BC偺拞揰傪M偲偡傞偲丄
丂丂丂AM丗GM=仮ABC丗仮GBC=俁丗侾 傛偭偰丄AG丗GM=俀丗侾
偲側傞丅
 亙傑側傇亜側傞傎偳丅廳怱偺傕偮堄枴傗丄偳偆偟偰廳怱偵傛傝拞慄偼俀丗侾偺斾偵暘偗傜傟傞偐偑傛偔傢偐傝傑偟偨丅
亙傑側傇亜側傞傎偳丅廳怱偺傕偮堄枴傗丄偳偆偟偰廳怱偵傛傝拞慄偼俀丗侾偺斾偵暘偗傜傟傞偐偑傛偔傢偐傝傑偟偨丅亙愭丂惗亜
偙偺嶰妏宍偺傛偆偵僗儔僀僗偟偨傕偺傪壛岺偟偰傕丄傕偲偺恾宍偺柺愊傗懱愊偼堦斒偵偼曄傢傜側偄丅偙傟傪僇僶儕僄儕偺尨棟偲偄偆傫偩丅
丂偝偁丄偦傟偱偼師偵拞恎偺側偄嶰妏宍偺廳怱傪媮傔偰傒傛偆丅亙傛偟偍亜
偱傕愭惗丄崱搙偺応崌偼柺愊偑側偄傢偗偱偡偐傜掁傝崌偆揰傕側偄傛偆側婥傕偡傞傫偱偡偑丅
 亙傑側傇亜嶰妏宍偺嶰曈偺廳偝傪峫偊傟偽偱偒傞傫偠傖側偄偐側丅
亙傑側傇亜嶰妏宍偺嶰曈偺廳偝傪峫偊傟偽偱偒傞傫偠傖側偄偐側丅亙偐偢巕亜
偩偗偳曈偼慄暘側傫偩偐傜廳偝偼偁傞偺偐側偁丠丅亙愭丂惗亜
偆傫丅偦偺偙偲偑幚偼廳梫側傫偩丅偙偙偱偼慄暘偵偼廳偝偼側偄偲偟偰恑傔偰偄偙偆丅亙傑側傇亜
偦偆偟偨傜廳偝偼側偄傢偗偩偐傜嶰妏宍偼偳偙偱偩偭偰掁傝崌偆偲傕峫偊傜傟傑偡傛丅亙愭丂惗亜
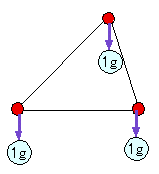
偦偆偩偹丅偦偙偱偩偹丅偙偺応崌偼嶰妏宍偵廳偝傪偮偗傞偨傔偵乽嶰妏宍偺俁偮偺捀揰偵摨偠廳偝傪傇傜壓偘傞乿偲峫偊偰丄僶儔儞僗傪偲偭偰傗傞傫偩丅椺偊偽奺捀揰偵侾g偺廳偝傪傇傜壓偘傟偽恾偺傛偆側嶰妏宍偑憐掕偝傟丄偙偺嶰妏宍偺掁傝崌偆揰偐傜廳怱傪峫偊偰偄偔丅
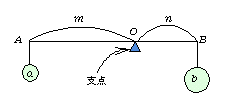
丂偙偙偱丄偪傚偭偲儌乕儊儞僩偲偄偆峫偊曽傪徯夘偟傛偆丅揤攭寁傝傪儌僨儖壔偡傞偲恾偺傛偆偵側傞丅偙偺偲偒揤攭偺椉抂偵僆儌儕傪傇傜壓偘傞偲偒丄揤攭傪巟偊傞揰( 巟揰)偐傜椉抂傑偱偺嫍棧偵僆儌儕傪妡偗偨抣傪巟揰偵娭偡傞儌乕儊儞僩偲偄偆丅恾偱偼丄am丆bn偺抣偵側傞偹丅偦偟偰偙偺俀偮偺抣偑摍偟偄偲偒揤攭偼偦偺巟揰偱掁傝崌偆偙偲偑抦傜傟偰偄傞丅椺偊偽丄a=3丆b=2偱偁傞側傜丄m丗n偼偳偆側傞偩傠偆丅
 亙傑側傇亜俀丗俁偵側傝傑偡丅
亙傑側傇亜俀丗俁偵側傝傑偡丅亙愭丂惗亜
偦偺捠傝丅偙偺峫偊曽傪巊偭偰拞恎偺側偄嶰妏宍偺廳怱傪媮傔偰傒傛偆偐丅傑偢丄曈BC偱儌乕儊儞僩傪峫偊傞偲BC偼拞揰M偱掁傝崌偆丅偦偺偲偒巟揰M偵偐偐傞廳偝偼偳傟偩偗偩傠偆丅亙傛偟偍亜
椉抂偺廳偝偺榓偱偡偐傜2g偱偡丅
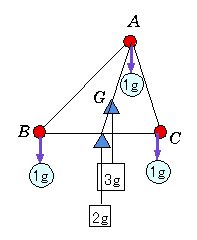 亙愭丂惗亜慄暘偵廳偝傪峫偊偰偼偄偗側偄偙偲偑偙偙偐傜暘偐傞偩傠偆丅師偵丄捀揰A偵偼1g偺僆儌儕偑傇傜壓偑傝丄揰M偵偼2g偺廳偝偑妡偐偭偰偄傞傢偗偩偐傜丄偱偼拞慄AM偼偄偭偨偄偳偙偱偮傝偁偆偩傠偆偐丅
亙愭丂惗亜慄暘偵廳偝傪峫偊偰偼偄偗側偄偙偲偑偙偙偐傜暘偐傞偩傠偆丅師偵丄捀揰A偵偼1g偺僆儌儕偑傇傜壓偑傝丄揰M偵偼2g偺廳偝偑妡偐偭偰偄傞傢偗偩偐傜丄偱偼拞慄AM偼偄偭偨偄偳偙偱偮傝偁偆偩傠偆偐丅亙傑側傇亜
拞慄AM偱儌乕儊儞僩傪峫偊偰傗傞偲乧乧丄偁偭丄俀丗侾偺斾偵暘偗傞揰偱掁傝偁偄傑偡丅亙愭丂惗亜
寢榑偑偱偨偹丅偡側傢偪廳怱G偼丄拞慄AM傪俀丗侾偺斾偵暘偗傞揰偩偲偄偆偙偲偩丅亙偐偢巕亜
偦偆偐丅巹偨偪偑儀僋僩儖側傫偐偱廗偭偨偺偼捀揰偵摨検偺廳偝傪壛偊偨偲偒偺廳怱偩偭偨偺偹丅亙愭丂惗亜
偆傫丄偩偐傜惓妋偵偄偆偲俁揰偺廳怱偲偄偭偨曽偑偄偄偐傕偟傟側偄丅亙傑側傇亜
偱傕丄壗偐庍慠偲偟側偄側偁丅偦傫側嶰妏宍側傫偰戞堦懚嵼偡傞偼偢側偄偟乧乧丅扨弮偵恓嬥傒偨偄側傕偺偱嶌傜傟偨嶰妏宍偱偼峫偊傜傟側偄偺偱偡偐丅亙傛偟偍亜
偦偆偡傞偲丄曈偵廳偝偑偁傞傢偗偩偐傜丄廳怱偺埵抲偑曄傢偭偰偟傑偆偠傖側偄丅亙愭丂惗亜
傑側傇偺拝娽揰偼柺敀偄偲巚偆側丅廳偝偺偁傞僼儗乕儉偱嶌傜傟偨嶰妏宍偺廳怱偼嫽枴怺偄榖戣偩偲巚偆丅掁傝崌偆揰偼偳偙偵偁傞偺偩傠偆偐丅亙惗搆払亜
乧乧乧亙偐偢巕亜
愭惗丄傂傚偭偲偟偨傜撪怱偱掁傝崌偆偺偱偼側偄偱偟傚偆偐丅亙傑側傇亜
偢偄傇傫撍攺巕傕側偄寢榑偩側丅傑偨偄偮傕偺偐偢巕偺捈姶偐偄丅亙偐偢巕亜
堘偆傢傛丅傑側傇偺摉偰偢偭傐偆偲堘偭偰巹偺偼偪傖傫偲偟偨崻嫆偑偁傞傢丅嶰妏宍ABC偺撪晹偺揰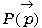 偺埵抲儀僋僩儖偼丄揰P偵傛偭偰暘偗傜傟偨俁偮偺嶰妏宍丄仮PAB丆仮PBC 丆仮PCA傪棙梡偟偰昞尰偱偒偨偱偟傚丅
偺埵抲儀僋僩儖偼丄揰P偵傛偭偰暘偗傜傟偨俁偮偺嶰妏宍丄仮PAB丆仮PBC 丆仮PCA傪棙梡偟偰昞尰偱偒偨偱偟傚丅亙傛偟偍亜
妋偐偦傟偧傟偺柺愊傪丄仮ABC=S丆仮PAB=S1丆仮PBC=S2丆仮PCA=S3 偲偡傞偲丄
丂丂丂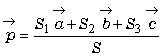
偩偭偨傛偹丅亙傑側傇亜
偦傫側偺偁偭偨偭偗丅亙偐偢巕亜
嶰妏宍偑嬒幙偺敄偄斅偱嶌傜傟偰偄傞偲偟偨傜丄偙偺幃偐傜廳怱偺埵抲儀僋僩儖傪媮傔傞偙偲偑偱偒傞偱偟傚丅亙傛偟偍亜
S1=S2=S3 偲偡傞偲丄妋偐偵廳怱偺埵抲儀僋僩儖偵堦抳偡傞偹丅
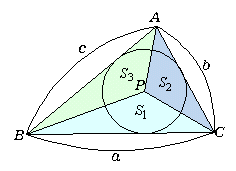 亙偐偢巕亜偩偐傜丄偒偭偲奺捀揰偺廳傒偑堘偆応崌傕偙偺揰偑掁傝崌偆偲偄偆堄枴偱偺廳怱偩偲巚偆偺丅摿偵僼儗乕儉偩偗偱嶌傜傟偨嶰妏宍偱偼丄揰P偑撪怱偱偁傟偽丄撪愙墌偺敿宎傪r偲偡傞偲丄
亙偐偢巕亜偩偐傜丄偒偭偲奺捀揰偺廳傒偑堘偆応崌傕偙偺揰偑掁傝崌偆偲偄偆堄枴偱偺廳怱偩偲巚偆偺丅摿偵僼儗乕儉偩偗偱嶌傜傟偨嶰妏宍偱偼丄揰P偑撪怱偱偁傟偽丄撪愙墌偺敿宎傪r偲偡傞偲丄
丂丂丂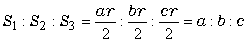
傛傝嶰妏宍偺柺愊偲僼儗乕儉偺挿偝偼斾椺偡傞傢偗偩偐傜丄
丂丂丂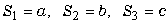
偲傒傞偲丄偙傟偐傜
丂丂丂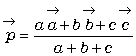
偙偺揰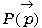 偼撪怱傪昞偟偰偄傞傢傛偹丅
偼撪怱傪昞偟偰偄傞傢傛偹丅亙愭丂惗亜
傑側傇丅偳偆巚偆丅
 亙傑側傇亜偆乕傫丅側傫偐傛偔暘偐傜側偄偗偳丄惓偟偄偲巚偄傑偡丅僀儊乕僕偲偟偰偼丄嶰妏宍偺撪愙墌偺敿宎傪彫偝偔偟偰傕丄掁傝崌偆揰偼曄傢傜側偄偲巚偆偐傜偳傫偳傫彫偝偔偟偰偄偗偽嶰妏宍傕弅彫偝傟丄嶰妏宍偼撪怱偵嬤偯偔傛偆側婥偑偟傑偡丅
亙傑側傇亜偆乕傫丅側傫偐傛偔暘偐傜側偄偗偳丄惓偟偄偲巚偄傑偡丅僀儊乕僕偲偟偰偼丄嶰妏宍偺撪愙墌偺敿宎傪彫偝偔偟偰傕丄掁傝崌偆揰偼曄傢傜側偄偲巚偆偐傜偳傫偳傫彫偝偔偟偰偄偗偽嶰妏宍傕弅彫偝傟丄嶰妏宍偼撪怱偵嬤偯偔傛偆側婥偑偟傑偡丅亙偐偢巕亜
壗偝丄傑側傇偺曽偑捈姶偵棅偭偰傞偠傖側偄偺丅亙愭丂惗亜
傑偁傑偁丅捈姶傪攏幁偵偟偪傖偄偗側偄丅悢妛偱偼捈姶偺屻偵榑棟惈偑偮偄偰偔傞偙偲偼傛偔偁傞丅嶰妏宍偺廳怱傕傑側傇偺僼儗乕儉嶰妏宍偺廳怱偺傾僀僨傾傕丄堘榓姶偲偄偆捈姶偐傜巒傑偭偨偙偲側傫偩偐傜丅
巐妏宍偺傊偦傪扵偦偆
 亙愭丂惗亜
亙愭丂惗亜
偱偼崱搙偼巐妏宍偺廳怱偵挧愴偟偰傒傛偆丅傕偆丄峌傔曽偼傢偐傞傛偹丅亙傛偟偍亜
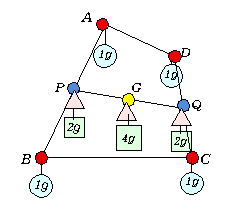
偼偄丅偙傟傕拞恎偺媗傑偭偨傕偺偲旂偩偗偺傕偺偺俀捠傝偑峫偊傜傟傑偡丅嵟弶偵丄杔払偑廗偭偨係揰偺廳怱丄偡側傢偪拞恎偺側偄応崌偱偡偑丄巐妏宍偺捀揰偵侾倗偺僆儌儕傪傇傜壓偘偰掁傝崌偄傪峫偊傑偡丅傑偢丄曈AB丆CD偱儌乕儊儞僩偺掁傝崌偄傪峫偊傞偲偦傟偧傟偺曈偺拞揰P丆Q偱掁傝崌偄丄俀倗偺廳偝偑壛傢傝傑偡丅嵟屻偵慄暘PQ偺偱儌乕儊儞僩傪峫偊偰丄偦偺拞揰G偑媮傔傞廳怱偲側傝傑偡丅亙愭丂惗亜
偙偺偙偲傪儀僋僩儖偱妋擣偟偰傒傛偆偐丅
巐妏宍偺捀揰傪丄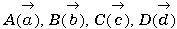 偲偡傞偲丄偦偺廳怱
偲偡傞偲丄偦偺廳怱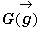 偺埵抲儀僋僩儖偼偳偆昞尰偱偒偨傠偆丅
偺埵抲儀僋僩儖偼偳偆昞尰偱偒偨傠偆丅亙傑側傇亜
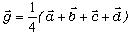 偱偡丅
偱偡丅亙愭丂惗亜
偙傟傪
丂丂丂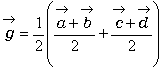
偲傒傞偲丄愭傎偳傛偟偍偑媮傔偨廳怱偵堦抳偡傞偙偲偑傢偐傞丅偱傕丄偙偺幃偺儀僋僩儖偺慻崌偣傪曄偊傞偲暿偺昞尰傕壜擻偵側傞傛偹丅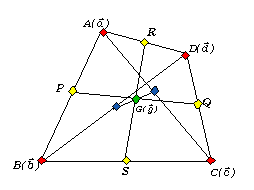 亙偐偢巕亜
亙偐偢巕亜
偼偄丅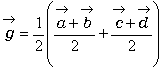 偲傒傞偲丄曈AD丆BC偺偦傟偧傟偺拞揰傪R丆S偲偡傞偲丄慄暘RS偺拞揰偲傕傒傟傑偡丅
偲傒傞偲丄曈AD丆BC偺偦傟偧傟偺拞揰傪R丆S偲偡傞偲丄慄暘RS偺拞揰偲傕傒傟傑偡丅亙傑側傇亜
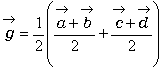 側傜懳妏慄偺拞揰傪寢傇慄暘偺拞揰偵傕側偭偰偄傞丅
側傜懳妏慄偺拞揰傪寢傇慄暘偺拞揰偵傕側偭偰偄傞丅亙愭丂惗亜
偦偆偩偹丅寢嬊丄係偮偺捀揰傪寢傇慄暘偺僶儔儞僗傪偲偭偰偄偔弴斣偵傛偭偰昞尰偑堘偭偰偔傞偲偄偆偙偲偩偹丅偠傖偁丄師偼敄斅偱嶌傜傟偨巐妏宍偺廳怱偩丅亙傑側傇亜
嶰妏宍偲摨偠傛偆偵丄係揰偺廳怱偵堦抳偡傞偲巚偄傑偡丅亙愭丂惗亜
杮摉偵偦偆偩傠偆偐丅係揰偺廳怱偲摨偠側傜丄偦偺揰偱巐妏宍偼摍柺愊偺恾宍偵暘妱偝傟丄掁傝崌偆偼偢偩偹丅揔摉側恾宍傪巚偄晜偐傋偰妋擣偟偰偛傜傫丅
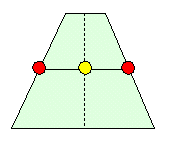 亙偐偢巕亜乧乧偁傟丠丄掁傝崌傢側偄傢丅
亙偐偢巕亜乧乧偁傟丠丄掁傝崌傢側偄傢丅亙愭丂惗亜
偐偢巕偼偳傫側巐妏宍傪峫偊偨偺丅亙偐偢巕亜
偼偄丅摍媟戜宍側傫偱偡偑丄柧傜偐偵柺愊偑堘偭偰偒傑偡丅亙傑側傇亜
偁傟丄杮摉偩丅嶰妏宍偱惉棫偟偨偙偲偼巐妏宍偱傕惉傝棫偮偲巚偭偨偺偵丄偍偐偟偄側丅偙偺応崌偼奼挘偱偒側偄傫偱偡偐丅亙愭丂惗亜
偙傟偼偹丅係揰偺懆偊曽偵栤戣偑偁傞傫偩丅暯柺忋偺係揰偱嶌傜傟傞捈慄恾宍偼巐妏宍俙俛俠俢偩偗偩傠偆偐丅亙傛偟偍亜
係揰偺寢傃曽偵傛偭偰懠偺恾宍傕峫偊傜傟傑偡丅亙愭丂惗亜
偦偆偩偹丅堉巕偺懌偺悢偱峫偊傞偲暘偐傝堈偄丅嶰杮懌偺堉巕偼侾杮偑懠偺傕偺傛傝抁偔偰傕彴偵僺僞偭偲懌偑偔偭晅偄偰埨掕偡傞偗偳丄巐杮懌偩偲偖傜晅偄偰偟傑偆偲偄偆偙偲偩丅偨偩丄偙傟偼暯柺忋偱峫偊傞偐傜偙傫側偙偲偑婲偒偰偔傞丅亙傑側傇亜
偳偆偄偆偙偲偱偡偐亙愭丂惗亜
傑側傇偺梊憐偟偨奼挘惈偼幚偼師尦偵懳偟偰惉棫偡傞傕偺側傫偩丅係揰傪嬻娫撪偺堎側傞揰偲峫偊偰傒傛偆丅偦偆偡傞偲偙偺係揰偼丄巐柺懱偺捀揰偲側傝埨掕偟偰偄傞丅亙傛偟偍亜
偦偆偐丅偡傞偲嬒幙側嵽椏偱嶌傜傟偨拞恎偺媗傑偭偨巐柺懱偺廳怱偵側傞偭偰偙偲偱偡偹丅
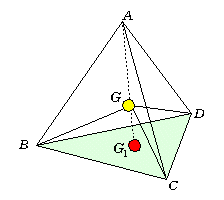 亙愭丂惗亜偦偺捠傝偩丅愭傎偳偺儀僋僩儖曽掱幃傪師偺傛偆偵曄宍偟偰傒傛偆丅
亙愭丂惗亜偦偺捠傝偩丅愭傎偳偺儀僋僩儖曽掱幃傪師偺傛偆偵曄宍偟偰傒傛偆丅
丂丂丂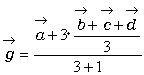
偙偆偡傞偲揰G偼嬻娫撪偱偳傫側揰偲傒傟傞偩傠偆丅亙偐偢巕亜
傑偢丄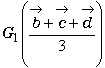 偼仮BCD偺廳怱偺埵抲儀僋僩儖傪昞偟偰偄傑偡丅偦偟偰丄慄暘AG1傪俁丗侾偺斾偵暘偗偨揰偑G偲偄偆偙偲偱偡丅
偼仮BCD偺廳怱偺埵抲儀僋僩儖傪昞偟偰偄傑偡丅偦偟偰丄慄暘AG1傪俁丗侾偺斾偵暘偗偨揰偑G偲偄偆偙偲偱偡丅亙愭丂惗亜
偡側傢偪丄捀揰偲偦偺懳柺偱偁傞嶰妏宍偺廳怱傪寢傇慄暘傪俁丗侾偺斾偵撪暘偟偨揰偑廳怱偲偄偆偙偲偩丅偦偆偡傞偲丄僇僶儕僄儕偺尨棟偵傛傝捈嶰妏悕偵壛岺偡傞偲丄巐柺懱ABCD偲G偱暘偗傜傟傞係偮偺巐柺懱偲偺懱愊斾偼俁丗侾偲偄偆偙偲偵側傞丅偟偨偑偭偰係偮偺巐柺懱偺懱愊(廳偝)偼傒側摍偟偔側傝揰G偱巐柺懱偼掁傝崌偆偙偲偵側傞丅
 亙傑側傇亜偪傖傫偲奼挘偱偒傞傫偩丅傗偭傁傝悢妛偼棤愗傜側偄傗丅
亙傑側傇亜偪傖傫偲奼挘偱偒傞傫偩丅傗偭傁傝悢妛偼棤愗傜側偄傗丅亙愭丂惗亜
偱偼丄杮戣偵栠偭偰暯柺忋偱巐妏宍偺掁傝崌偆揰傪媮傔偰尒傛偆丅亙偐偢巕亜
偙傟傕儌乕儊儞僩傪峫偊傟偽偄偄偺偱偼側偄偱偟傚偆偐丅傑偢丄巐妏宍傪懳妏慄AC偱俀偮偺嶰妏宍丆仮ABC丆仮ACD偵暘偗傑偡丅偙偺偦傟偧傟偺嶰妏宍偼廳怱G1 丆G2偱掁傝崌偆傢偗偱偡偐傜丄偦偺廳怱傪寢傇慄暘G1G2偱儌乕儊儞僩偺掁傝崌偄傪峫偊傞傫偱偡丅
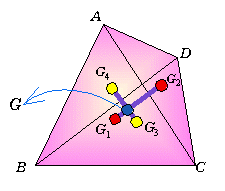 亙傛偟偍亜慄暘偺椉抂偵嶰妏宍偺柺愊傪昞偡僆儌儕傪傇傜壓偘傞偲偄偆偙偲偩偹丅摉慠偦偺慄暘忋偵掁傝崌偆揰偑偁傞偼偢偩偹丅
亙傛偟偍亜慄暘偺椉抂偵嶰妏宍偺柺愊傪昞偡僆儌儕傪傇傜壓偘傞偲偄偆偙偲偩偹丅摉慠偦偺慄暘忋偵掁傝崌偆揰偑偁傞偼偢偩偹丅亙偐偢巕亜
偦偆丅偦偟偰偹丅崱搙偼懳妏慄BD偱俀偮偺嶰妏宍丄仮BCD丆仮ABD偵暘妱偟偰偦傟偧傟偺廳怱G3 丆G4傪寢傃丄愭傎偳偺慄暘G1G2偲偺岎揰傪媮傔傞偲偦偺揰偑巐妏宍偺廳怱偵側傞偼偢偩傢丅亙傑側傇亜
傊偦偲傊偦傪懌偟偰傊偦傪媮傔傞偭偰偙偲偐丅偦偆偟偨傜偙偆峫偊偰傕柺敀偄偲巚偆側丅愭惗偑嫵偊偰偔傟偨僇僶儕僄儕偺尨棟傪棙梡偡傞傫偩丅亙愭丂惗亜
傑側傇偄偭偰偛傜傫丅亙傑側傇亜
傑偢丄懳妏慄BD偵偦偭偰(暯峴偵)捀揰A傪曈CB偺墑挿忋傑偱偢傜偟丄嶰妏宍ACD傪嶌傝傑偡丅偦偟偰偦偺廳怱傪G1偲偡傞偲丄傕偲傕偲偺巐妏宍偺廳怱偼G1傪拞慄DG1忋偵僗儔僀僪偟偨偲偙傠偵偁傞偼偢偱偡丅摨條偵丄崱搙偼捀揰D傪懳妏慄AC 偵偦偭偰偢傜偟丄嶰妏宍ABD偺廳怱G2傪傕偲傔傞偲丄拞慄AG2忋偵廳怱偑偁傞偙偲偵側傝傑偡丅偟偨偑偭偰偙偺俀偮偺拞慄偺岎揰偑巐妏宍偺廳怱偵側傝傑偡丅
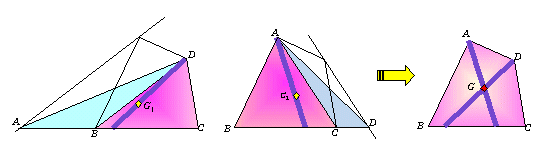
亙偐偢巕亜
側傞傎偳偹丅偦偆偄偆峫偊曽傕偱偒傞偺偹丅亙傛偟偍亜
偱傕偳偪傜偺曽朄偵偟偰傕丄偦傟偼嶌恾偲偟偰廳怱偺埵抲偑挷傋傜傟傞偩偗偱偁偭偰丄嶰妏宍偺傛偆偵拞慄偺斾偺抣偲偟偰廳怱偑媮傑傞傢偗偱偼側偄偱偡傛偹丅亙愭丂惗亜
妋偐偵偦偆偩偹丅偦傟偲係揰偺廳怱偲偺娭學傕婥偵側傞偲偙傠偩偹丅偦傟偱偼嵟屻偵偦偺偙偲偵偮偄偰挷傋偰傒傛偆偐丅巐妏宍傪懳妏慄偱暘偗偰偱偒傞嶰妏宍丄仮ABC丆仮ACD丆仮ABD丆仮BCD偺偦傟偧傟偺廳怱偺埵抲儀僋僩儖傪
丂丂丂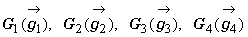
偲偟傛偆丅偄傑丄慄暘G1G2 偼偦偺椉抂偱嶰妏宍ABC丆嶰妏宍ACD偺柺愊偵憡摉偡傞(斾椺偡傞)廳傒偑妡偐偭偰偄傞丅
丂偟偨偑偭偰丄巐妏宍偺廳怱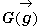 偼丄巐妏宍ABCD偺柺愊傪S偲偡傞偲丄
偼丄巐妏宍ABCD偺柺愊傪S偲偡傞偲丄
丂丂丂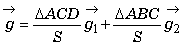
偱梌偊傜傟傞丅偙偙偱丄G1丆G2 偺埵抲儀僋僩儖傪偦傟偧傟媮傔偰傒傛偆丅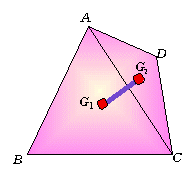 亙傑側傇亜
亙傑側傇亜
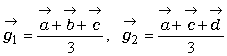 偲側傝傑偡丅
偲側傝傑偡丅亙愭丂惗亜
偟偨偑偭偰丄
丂丂丂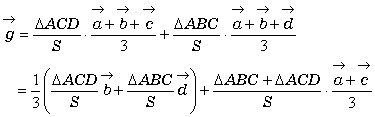
偲側傞丅
偙偙偱丄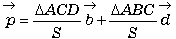 偲偍偔偲丄揰
偲偍偔偲丄揰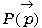 偼偳傫側揰偺埵抲儀僋僩儖傪昞偟偰偄傞偐挷傋偰傒傛偆丅
偼偳傫側揰偺埵抲儀僋僩儖傪昞偟偰偄傞偐挷傋偰傒傛偆丅
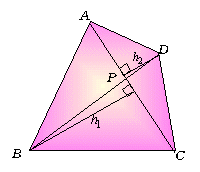
捀揰B丆D偐傜懳妏慄AC偵壓傠偟偨悅慄偺挿偝傪h1丆h2 偲偟丄仮ABC丆仮ACD偺柺愊傪昞尰偡傞偲偳偆側傞偩傠偆偐丅
 亙傛偟偍亜
亙傛偟偍亜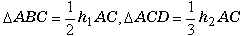 偲側傝傑偡丅
偲側傝傑偡丅亙愭丂惗亜
偩偐傜丄巐妏宍偺懳妏慄偺岎揰傪P偲偡傞偲丄
丂丂丂仮ABC丗仮ACD=h1丗h2=BP丗PD
偲側傞丅亙傛偟偍亜
偦偆偡傞偲丄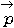 偼懳妏慄偺岎揰P偺埵抲儀僋僩儖偲偄偆偙偲偱偡偹丅
偼懳妏慄偺岎揰P偺埵抲儀僋僩儖偲偄偆偙偲偱偡偹丅亙愭丂惗亜
偦偺捠傝丅傛偭偰偙傟偐傜丄
丂丂丂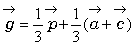 丂丂乧乧乧乧嘆
丂丂乧乧乧乧嘆
偑摼傜傟傞丅
偱偼軅羵絺瓝瘲l偵峫偊偰丄仮ABD偲仮BCD偵暘偗偰廳怱G偺埵抲儀僋僩儖傪媮傔傞偲偳偆側傞偩傠偆偐丅亙偐偢巕亜
懳妏慄偺岎揰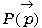 偼曄傢傝傑偣傫偐傜丄
偼曄傢傝傑偣傫偐傜丄
丂丂丂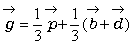 丂丂乧乧乧乧嘇
丂丂乧乧乧乧嘇
偲側傝傑偡丅亙愭丂惗亜
偩偄傇寢榑偵嬤偯偄偰偒偨丅偙偺俀幃嘆丄嘇傪曈乆壛偊偰傒傛偆丅
丂丂丂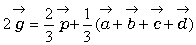 丂丂乧乧乧乧嘊
丂丂乧乧乧乧嘊
丂偝偰丄偙偙偱丄塃曈偺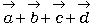 偼壗傪堄枴偟偰偄傞偩傠偆丅
偼壗傪堄枴偟偰偄傞偩傠偆丅
 亙傑側傇亜偁偭丄偙傟偭偰傕偟偐係揰偺廳怱偵娭學偟偰傑偡偐丅偊乕偭偲丄係揰偺廳怱偺埵抲儀僋僩儖傪
亙傑側傇亜偁偭丄偙傟偭偰傕偟偐係揰偺廳怱偵娭學偟偰傑偡偐丅偊乕偭偲丄係揰偺廳怱偺埵抲儀僋僩儖傪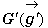 偲偡傞偲丄
偲偡傞偲丄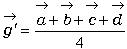 偱偡偐傜丄
偱偡偐傜丄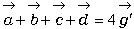 偱偡丅
偱偡丅亙愭丂惗亜
偦傟偱偼偙傟傪嘊偵戙擖偟偰惍棟偟偰傒傛偆丅
丂丂丂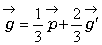
偲側傞丅偙偺幃偐傜廳怱偺埵抲偼偳偙偵偁傞偲偄偊傞偩傠偆丅亙傑側傇亜
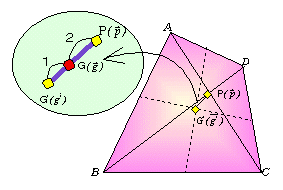
偼偄丄巐妏宍偺懳妏慄偺岎揰傪P丄巐妏宍偺係捀揰偺廳怱傪G'偲偡傞偲丄巐妏宍偺廳怱偼慄暘PG'傪俀丗侾偺斾偵撪暘偡傞揰偲偄偆偙偲偵側傝傑偡丅
惁偄丅慛傗偐側寢壥偵側傞傫偱偡偹丅
偁偲偑偒
丂杮峞偺昞戣偼丄乽岆庤媄乿偱偡偐傜撪梕偵偼岆傝偑偁傝傑偡丅偨偩丄塕(岥偑嬻偟偄偲彂偔)偺偮傕傝偼側偔丄幐攕偲夝庍偟偰偄偨偩偗傟偽偲巚偄傑偡丅尵梩傪偐偊傟偽婾傝(恖偺堊偲彂偔)偲偄偆偙偲偱偡丅扤偵懳偟偰偺婾傝偐偲偄偆偲丄傑偁嵟戝偺僞乕僎僢僩偼帺暘偵懳偟偰偺夲傔偺堄枴偵側傝傑偟傚偆偐丅偦偆巚偭偰杮暥傪撉傫偱偄偨偩偗傟偽岾偄偱偡丅
丂側偍丄婾傝偺晹暘偵偮偒傑偟偰偼偦偺偆偪傑偲傔傞梊掕偱偡偑丄巹偑堄恾偟偨婾傝埲奜偵丄巹偑堄恾偱偒側偐偭偨婾傝傕偁傞偐傕偟傟傑偣傫丅偛堄尒傪巉偊傟偽偲巚偄傑偡丅


 亙偐偢巕亜
亙偐偢巕亜 亙愭丂惗亜
亙愭丂惗亜 亙傛偟偍亜
亙傛偟偍亜 亙傑側傇亜
亙傑側傇亜 亙傛偟偍亜
亙傛偟偍亜 亙傑側傇亜
亙傑側傇亜 亙傑側傇亜
亙傑側傇亜 亙傑側傇亜
亙傑側傇亜 亙愭丂惗亜
亙愭丂惗亜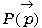 偺埵抲儀僋僩儖偼丄揰P偵傛偭偰暘偗傜傟偨俁偮偺嶰妏宍丄仮PAB丆仮PBC 丆仮PCA傪棙梡偟偰昞尰偱偒偨偱偟傚丅
偺埵抲儀僋僩儖偼丄揰P偵傛偭偰暘偗傜傟偨俁偮偺嶰妏宍丄仮PAB丆仮PBC 丆仮PCA傪棙梡偟偰昞尰偱偒偨偱偟傚丅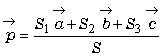
 亙偐偢巕亜
亙偐偢巕亜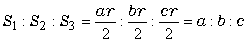
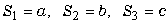
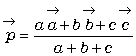
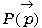 偼撪怱傪昞偟偰偄傞傢傛偹丅
偼撪怱傪昞偟偰偄傞傢傛偹丅 亙傑側傇亜
亙傑側傇亜 亙愭丂惗亜
亙愭丂惗亜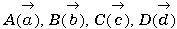 偲偡傞偲丄偦偺廳怱
偲偡傞偲丄偦偺廳怱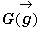 偺埵抲儀僋僩儖偼偳偆昞尰偱偒偨傠偆丅
偺埵抲儀僋僩儖偼偳偆昞尰偱偒偨傠偆丅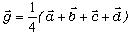 偱偡丅
偱偡丅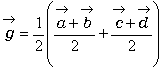
 亙偐偢巕亜
亙偐偢巕亜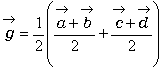 偲傒傞偲丄曈AD丆BC偺偦傟偧傟偺拞揰傪R丆S偲偡傞偲丄慄暘RS偺拞揰偲傕傒傟傑偡丅
偲傒傞偲丄曈AD丆BC偺偦傟偧傟偺拞揰傪R丆S偲偡傞偲丄慄暘RS偺拞揰偲傕傒傟傑偡丅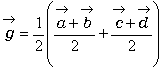 側傜懳妏慄偺拞揰傪寢傇慄暘偺拞揰偵傕側偭偰偄傞丅
側傜懳妏慄偺拞揰傪寢傇慄暘偺拞揰偵傕側偭偰偄傞丅 亙偐偢巕亜
亙偐偢巕亜 亙愭丂惗亜
亙愭丂惗亜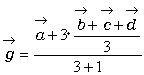
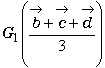 偼仮BCD偺廳怱偺埵抲儀僋僩儖傪昞偟偰偄傑偡丅偦偟偰丄慄暘AG1傪俁丗侾偺斾偵暘偗偨揰偑G偲偄偆偙偲偱偡丅
偼仮BCD偺廳怱偺埵抲儀僋僩儖傪昞偟偰偄傑偡丅偦偟偰丄慄暘AG1傪俁丗侾偺斾偵暘偗偨揰偑G偲偄偆偙偲偱偡丅 亙傑側傇亜
亙傑側傇亜 亙傛偟偍亜
亙傛偟偍亜
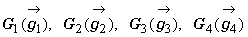
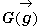 偼丄巐妏宍ABCD偺柺愊傪S偲偡傞偲丄
偼丄巐妏宍ABCD偺柺愊傪S偲偡傞偲丄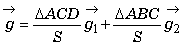
 亙傑側傇亜
亙傑側傇亜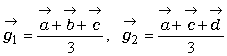 偲側傝傑偡丅
偲側傝傑偡丅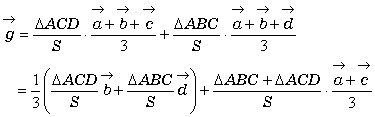
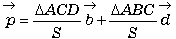 偲偍偔偲丄揰
偲偍偔偲丄揰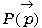 偼偳傫側揰偺埵抲儀僋僩儖傪昞偟偰偄傞偐挷傋偰傒傛偆丅
偼偳傫側揰偺埵抲儀僋僩儖傪昞偟偰偄傞偐挷傋偰傒傛偆丅 亙傛偟偍亜
亙傛偟偍亜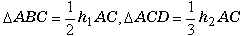 偲側傝傑偡丅
偲側傝傑偡丅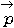 偼懳妏慄偺岎揰P偺埵抲儀僋僩儖偲偄偆偙偲偱偡偹丅
偼懳妏慄偺岎揰P偺埵抲儀僋僩儖偲偄偆偙偲偱偡偹丅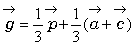 丂丂乧乧乧乧嘆
丂丂乧乧乧乧嘆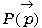 偼曄傢傝傑偣傫偐傜丄
偼曄傢傝傑偣傫偐傜丄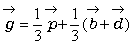 丂丂乧乧乧乧嘇
丂丂乧乧乧乧嘇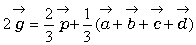 丂丂乧乧乧乧嘊
丂丂乧乧乧乧嘊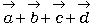 偼壗傪堄枴偟偰偄傞偩傠偆丅
偼壗傪堄枴偟偰偄傞偩傠偆丅 亙傑側傇亜
亙傑側傇亜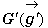 偲偡傞偲丄
偲偡傞偲丄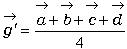 偱偡偐傜丄
偱偡偐傜丄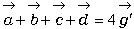 偱偡丅
偱偡丅