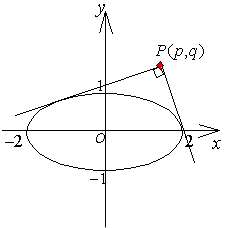
| ex) 楕円 x2+4y2=4 について、 (1) 楕円の外部の点 P(p，q)から、この楕円に引いた２本の接線が直交するような点 P の軌跡を求めよ。 (2) 楕円が直線 y=x+k と交わるとき、楕円によって切り取られる線分の中点の軌跡を求めよ。 |
＜先 生＞まず(1)だ。接線上の点はすでに与えられているから、接線の傾きを m として、進めてみようか。
＜よしお＞そうすると接線の方程式は y=m(x-p)+q ということですね。
＜まなぶ＞そうそう、それを楕円の方程式に代入するってことだよね。
＜先 生＞とにかく代入して整理してみよう。かず子どうなる。
＜かず子＞ x2+4{m(x-p)+q}2=4だから
x2+4{m2x2+2m(-pm+q)x+(-pm+q)2}=4
整理して、
(4m2+1)x2+8m(-pm+q)x+4(-pm+q)2-4=0
となります。
＜先 生＞では、このあとはどうすればいいだろうか。
＜まなぶ＞接するのだから、かず子の求めた２次方程式が重解をもてばいいんですよね。
＜先 生＞そうだ。まなぶのいう通りだ。
＜よしお＞判別式を D とすると、この場合は x の１次の項が係数が偶数だから、D/4 の方がいいですね。
D/4=16m2(-pm+q)2-(4m2+1){4(-pm+q)2-4}
これ、大変そうですね。
＜まなぶ＞でも、簡単にまとまりそうな気がするな。
＜かず子＞どうしてそう思うの。
＜まなぶ＞だって、方程式は重解をもつから判別式 D=0 だよね。でもいまよしおが整理した式は m の４次式にみえるじゃないか。接線は２本しか引けない訳だから、傾き m が４つもでてくるのはおかしいよ。だから、３次、４次の項は計算すると消えるのではないだろうか。
＜先 生＞ほんとに近頃のまなぶは冴えているというか、何というか……。まっ、とにかくまなぶの予想は正しい。そこのところを考えて計算してごらん。
＜よしお＞なんとなく分かるような気がします。(-pm+q)2 をうまく扱うんですね。
D/4=16m2(-pm+q)2-16m2(-pm+q)2+16m2-4(-pm+q)2+4
=16m2-4(-pm+q)2+4
=(16-4p2)m2+8pqm+(4-4q2)
先生、これでいいんでしょうか。
＜先 生＞ＯＫだ！。ここで重解を持つから D=0 ということだったから、
(16-4p2)m2+8pqm+(4-4q2)=0
(4-p2)m2+2pqm+(1-q2)=0
最後に、２接線が直交することを利用しよう。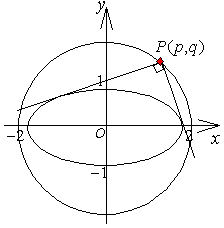
＜かず子＞直交条件は、接線の傾きどうしの積が－１ということですね。だから……、解と係数の関係ですね。２解を α，βとすると、
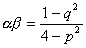
そして、αβ=-1 より、
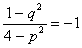
これから、 p2+q2=5 が得られます。
＜まなぶ＞そうすると、点 P(p，q) の軌跡を考えるわけだから、これが正体ですね。
中心が原点、半径 √5 の円が求める軌跡になります。
＜先 生＞正確には y軸に平行な接線は直線の標準形では表現できないからその場合も確認する必要はあるけど、考え方としてはいいだろう。どうだろう。けっこうしんどい計算だと思わないか。
＜かず子＞ええ。まなぶが予想してくれなかったら大変な計算をする羽目になっていたわ。まなぶ。ポイント上げたね。
＜まなぶ＞なんの。実力さ。でも、先生、これで終りじゃないんでしょ。この程度の話じゃ先生らしくないですよ。
＜先 生＞最近、まなぶに先読みされてしまうことが多くて先生落ち込むなあ。残念ながら、その通りだ。今日の本当のテーマはこれを円の性質を利用して解くことなんだ。
＜まなぶ＞円ですか。でも先生、今は楕円の問題ですよ。
＜先 生＞やっとまなぶらしい質問がでたな。円は楕円の特殊な場合と考えてみればいい。楕円を適当に引っ張ったりつぶしたりして円に変えてみよう。どう変形すればいいだろうか。
＜よしお＞ y軸方向に２倍に引っ張るか、x軸方向に半分に縮めればいいと思います。
＜先 生＞では、y軸方向に伸ばして円にしてみよう。円の方程式はどうなる。
＜まなぶ＞ x2+y2=4 です。
＜先 生＞次に直線 y=m(x-p)+q を伸ばしてみよう。一定比率で 軸方向に伸ばすから直線に移されるけど、ではどんな式になるだろうか。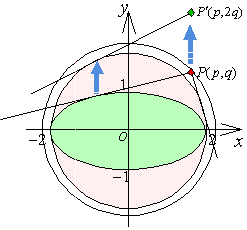
＜生徒達＞ ………。
＜先 生＞直線は、点と傾きが与えられれば決まることを利用しよう。
＜かず子＞分かりました。点(p，q) は、y座標が２倍になるから (p，2q) 、傾きmは、2m となります。
＜先 生＞そうだね。結局、直線の方程式は、y=2m(x-p)+2q ということだね。さあ、あとは、この円と直線について問題を考えていけばいい。まず直線は円に接することからなにを調べればいいだろう。
＜かず子＞判別式では先ほどと同じ計算になってしまいますよね。そうすると……、点と直線の距離ですね。
＜先 生＞その通り。円の中心と直線との距離が円の半径に等しければいい。さて、どんな計算になる。
＜よしお＞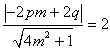
より、両辺を平方して整理すると、
(-pm+q)2=4m2+1
∴ (p2-4)m2-2pqm+(q2-1)=0
＜まなぶ＞そして、最後はまた解と係数の関係ですね。この方程式の２解は直線の傾きを表していたから、傾きどうしの積を考えて、
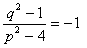
∴ p2+q2=5
なるほど。先ほどの面倒な計算がないですね。
＜先 生＞まなぶに一番美味しいところを取られてしまったな。では同様に考えて(2)もやってみよう。まず直線 y=x+k はどんな直線に変わるだろうか。
＜よしお＞傾き、y切片ともにy軸方向に２倍になるから、y=2x+2k です。
＜先 生＞では楕円と直線が交わったときの弦の中点は、円と直線ではどうなるだろう。
＜かず子＞この場合、y軸方向に引き伸ばしているから、x軸方向は変わらず、弦の中点もやっぱり同じ中点になります。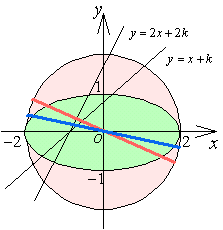
＜先 生＞整理しよう。結局、直線 y=2x+2k と円 x2+y2=4 が２点で交わったとき、その中点の軌跡を求めろという問題になるね。どうなるだろうか。
＜まなぶ＞あれっ！。それって先生、弦が直径であるとき、中点は円の中心ですよね。
＜かず子＞まなぶ、何を言いたいの。
＜まなぶ＞もうすでに、軌跡の方程式を求まっているってことさ。だって、直線 y=2x+2k に垂直で、原点を通る直線は弦の垂直二等分線になりますよね。だから直線 y=-x/2ですね。
＜先 生＞また、美味しいところ、まなぶに奪われてしまった。じゃあ、あとは軌跡の限界だ。
＜よしお＞じゃ、それはぼくがやります。直線 y=-x/2 と x2+y2=4 との交点 座標を求めて、
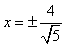
だから、軌跡は、
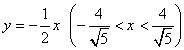
となります。
＜先 生＞そして最後にこれを楕円と直線の関係に戻してやれば終りだ。
今度は、 軸方向に半分に縮めてやればいいね。
＜かず子＞そうすると、定義域は変わらないから、軌跡は、
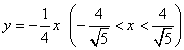
ということですね。でも、先生、何か今日は、「解けた！」っいう成就感がいまひとつ薄いのですけれど。
＜先 生＞うーん。実は先生も同じように感じる。最近問題解決のみんなの役割分担が微妙にずれているような気がするだが、どう思う、まなぶ。
＜まなぶ＞何を先生がいいたいのか分からないけれど、僕には単にいままで歪んでいた楕円が自然に円に戻っただけのことだと思うけれど。
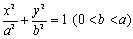に対して、円 x2+y2=a を楕円の補助円といいますが、ほとんどの楕円に関する問題は補助円を考え、円特有の性質を使えば簡単に求められます。本文のex)について、補足しましょう。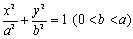に２接線が直交するようにある点から接線を引くと、その軌跡は次のようになります。
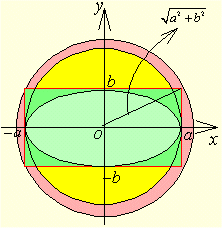点を (X，Y)とし、接線の方程式を y=m(x-X)+Y とします。楕円を補助円にするために、y軸方向にa/b倍すると直線の方程式は、
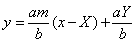となります。円の中心と直線との距離は円の半径 に等しいから、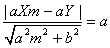
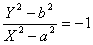
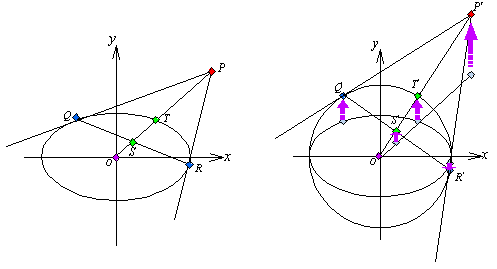
| 楕円外の極 P に対して、線分 OP と極線、楕円との交点をそれぞれ S，Tとすると、 OS・OP=OT2 が成り立つ。 |
この関係についても、楕円の補助円を利用すると簡単に説明できます。
楕円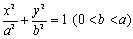の補助円 x2+y2=a2 を考えます。
各点 P，S，Tおよび、２接点 Q，R をy軸方向に a/b倍した点をそれぞれ、P'，S'，T'，Q'，R' とします。
このとき上の関係は、
OS'・OP'=OT'2………(＊)
なる関係に置き換えられます。この関係は次のように示されます。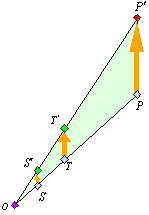
△OP'Q'∽△OQ'S'より、
OQ'：OS'=OP'：OQ'
∴ OS'・OP'=OQ'2=OT'2
ここで、明らかに
OP：OS：OT=OP'：OS'：OT'
が成立することから性質が証明できます。
ところで、補助円における関係(＊)を
O を中心として、点S と点P は反転の関係にある
といいます。すなわち、楕円においても反転の関係は保存されることを表しているわけです。
また、ex(2)についてですが、補助円においては、「円の中心は弦の垂直二等分線上にある」という事実に帰着します。これは２接点を結ぶ直線でもあるわけですから、楕円においても２接点を通る(原点を通る)直線がその軌跡となるわけです。
次に、補助円による楕円問題の解法を別の問題でもう少し扱ってみましょう。
ex1) 楕円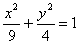 に内接する三角形・四角形のそれぞれの面積を最大値を求めよ。 |
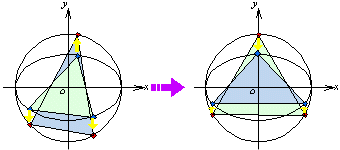補助円は、x2+y2=9 となり、円に内接する三角形・四角形の面積の最大値を求めればよいことになります。
三角形の場合は、正三角形、四角形の場合は、長方形のときに面積が最大となるのは明らかです。
正三角形の面積 Ｓ1は、
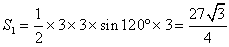
よって、求める三角形の面積の最大値は
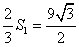
となります。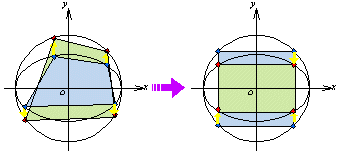
同様に四角形の面積 は、
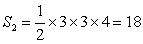
よって、求める四角形の面積の最大値は、
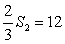
となります。
また、(2)については補助円を考えることでその軌跡は２接点を通る直線(原点を通る)であることは明らかとなります。
次に、補助円による解法を別の問題でもう少し扱ってみましょう。
ex2) 点A(2，0) から引いた直線が楕円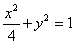 によって切り取られる弦の中点の軌跡を求めよ。 |
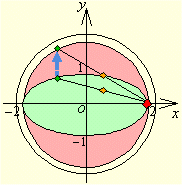楕円の補助円は、x2+y2=4 となります。また、点A(2，0) は変わりませんから、点A から引いた直線を y=m(x-2) とすると、この直線と原点を通って垂直な直線 y=-x/mとの交点が弦の中点になります。２式を辺辺かけて m を消去すると、
y2=-x(x-2)
∴ (x-1)2+y2=1
となります。最後にこれを y軸方向に 1/2倍したもので、楕円の内部にある点が求める軌跡です。
∴ (x-1)2+4y2=1 (ただし、(2，0)は除く)
これは、もとの楕円を x軸方向に１平行移動したものであることが分かります。
| ex3) 直線 y=2x+k が楕円 4x2+9y2=36 によって切り取られる弦の長さが４となるとき、実数 k の値を求めよ。 |
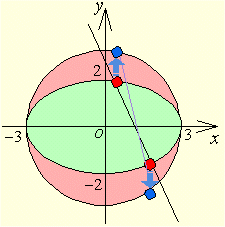補助円は x2+y2=9 であり、直線は、y=3x+3k/2 となります。
いま、直線と楕円の交点の x座標を α，βとすると、
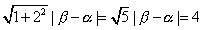
よって補助円の弦の長さは、
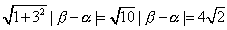
したがって、原点と弦までの距離は、
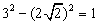
これから、原点と、直線 6x-2y-3k=0 との距離を求めて、
∴ 
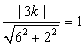
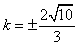
最後に、補助円を利用して楕円の接線の方程式を求めてみましょう。
楕円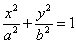 について、①傾き m の接線の方程式は 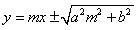 ②楕円上の点 (x1，y1) における接線の方程式は  |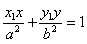
①の証明)
補助円 x2+y2=a2 にたいして、接線の方程式 y=mx+n は、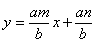
と表される。補助円の中心である原点と直線との距離は円の半径に等しいから、
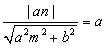
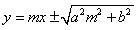∴ より公式を得る。
②の証明)
補助円 x2+y2=a2 に対して、楕円の接点 (x1，y1)は、補助円の接点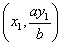 
に移される。
よって円周上の点 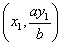における接線は、
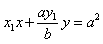。これを 軸方向に b/a 倍すると、
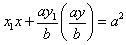
より公式を得る。