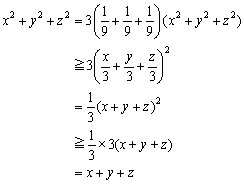|
ex) a��0�Cb��0�̂Ƃ��A���̕s�������ؖ�����B �@(1) 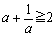 �@(2) 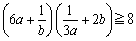 �@(3) 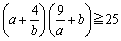
|
�������q���܂�(1)�ˁB����͊ȒP����B
�@�@�@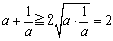
���������́A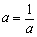 ���Aa=1�̂Ƃ��ł��B
���Aa=1�̂Ƃ��ł��B
���悵��������(2)�ł��ˁB
�@�܂��A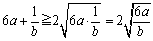
�@���l�ɁA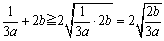
�@�Q����ӁX�����āA
�@�@�@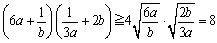
���������́A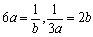 ���A6ab=1�̂Ƃ��ł��B
���A6ab=1�̂Ƃ��ł��B
����@���������͂Ȃ��Ȃ��������ˁB�ł͍Ō��(3)���B�܂ȂԂ̔Ԃ��ȁB
���܂Ȃԁ����[��B�Ȃ��ȗ\��������B
�������q���ǂ����āH�B
���܂Ȃԁ������āA���܂�ɏ����߂��邾��B���������Ƃ��͂�����(3)�ɉ������Ƃ���������Ɍ��܂��Ă���B�ŏ��ɖ��������Ă����悩�����B
����@�����ȂɃu�c�u�c�����Ă���낤�B���������Ă����B
���܂Ȃԁ����[��B�ꌩ(2)�Ɠ����Ȃ��ǁc�c�A�܂�������B
�@�܂��A
�@�@�@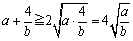
�@���l�ɁA
�@�@�@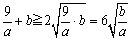
�@�Q����ӁX�����āA
�@�@�@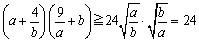
�@��[�A����ς肾�B�͂߂�ꂽ�B�E�ӂ̒l������Ă��Ă���B
����@��������l�����̈������Ƃ��B�ł��A�m���ɉE�ӂ̒l������Ă���ˁB�ǂ����Ă����Ȃ������l���Ă����B
���悵�����܂ȂԂ͖̉l�Ɠ����ł�����Ԉ���Ă͂��Ȃ��ł���ˁB
���܂Ȃԁ��悵���̉Ɣ�r�����̂͂�����ƃV���N�����ǁA�l���ԈႢ�͂Ȃ��悤�Ɏv�����ł�����ǁB
����@���������A�����܂ł͊ԈႢ���Ȃ��B
���܂Ȃԁ���H�A��������Ǝ����炪�ԈႢ�Ƃ������Ƃł����B���̌�́A���������̏������l�����ł���ˁB
�@�����E���敽�ς��Ƃ����Q�������������������Aa=4/b �� 9/a=b �ł���ˁB�����A�������B
�������q���ǂ������́A�����킩�����́B
���܂Ȃԁ������āA���������͂��ꂼ��̕s��������ab=4�Cab=9 ���ĂłĂ��邾��B�������a�Cb �ȂȂ�����Ȃ����B
����@�������̒ʂ肾�B�L���u���v�́A�u���܂��́��̂����ꂩ���������Ă���v�Ƃ����Ӗ���\���Ă���B�����灆�̂���Q�̕s������ӁX�����Ă��K��������������������Ƃ͌���Ȃ��B
�@���āA��������Ƃ܂��U��o���ɖ߂��Ă��܂������ƂɂȂ�ȁB���ǂ��̕s�����̏ؖ��͂ǂ�����������낤�B
���悵�������ꂱ���A�U��o���ɖ߂������Ǝv���܂��B�s�����̈�ʓI�ؖ����@�͂��Ƃ��ƁA(����)�|(�E��)���v�Z���������ׂ�悩�����킯�ł�����A���̏ꍇ�A
�@�@�@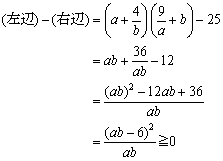
�ƂȂ�܂��B�Ō�ɓ��������ł����Aab=6 �̂Ƃ��ł��B
���܂Ȃԁ��Ȃ�قǁB�ł�������Ɣ�������ȁB�����č����̎��Ƃ́A�����E���敽�ς̕��K���Đ搶�͂����Ă����킯������A�悵���̂������Ƃ܂������g���ĂȂ����ƂɂȂ邾��B
�������q�����v��B�悵�����W�J�������̒��ŁA�Q���� ab �� 36/ab �ɑ����E���敽�ς̊W���g�����Ȃ����ȁB
�@�@�@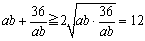
�@������A(����)�|(�E��)��0 ���������B
����@��������ƁA���_���ł��ˁB
���܂Ȃԁ����[��H�A�ł��l�͔[�������Ȃ��ȁB
�������q�������̂܂ȂԁA�����^��[����ˁB�������Ȃ́B
���܂Ȃԁ������ĂˁB�����q�̂悤�ɂ��Ίm���ɑ����E���敽�ς̊W����ؖ��ł��邯�ǁA�l�I�ɂ͂悵���̍ŏ��ɂ�����̕���������₷���Ǝv���ȁB���������E���敽�ς̊W�����Ďg���Ă���悤�Ȉ�ۂ�����ǁB
�������q������͂��A���̖��͑����E���敽�ς̊W���g���Ƃ��ɂ́A���������̏ꍇ�܂ōl���Ȃ���s�\�������Ă��Ƃ��Ӑ}���Ă����肾���Ă��Ƃł���B
���܂Ȃԁ������āA�ǂ̕s�����̏ؖ��ł����������ׂ�͓̂�����O�̂��Ƃ���B
�������q������́A���������ǁc�c�A�����Ă݂�Α����E���敽�ς͕֗��Ȍ��������Ǐ��n�̌����Ă��Ƃ��������̂���Ȃ�������B
���܂Ȃԁ��������Ȃ��B
����@�����Ղ��Ĉ������ǁA���́A�搶���܂ȂԂ̈ӌ��Ɏ^���ȂB
�������q�������I
����@�����{���́A�搶�A�����E���敽�ϕs�v�_�҂ȂB
���܂Ȃԁ����ꂵ���B�搶�Ə��߂ċC�������ʂ��������悤�ȋC������B�l����X�����v���Ă���ł��B�����āA���ӂ���E�ӂ������ĕ�����������Ώؖ��ł����Ⴄ����A�����E���敽�ςȂ�ĊW��������w�Ɏg���K�v�Ȃ�ĂȂ��ł���ˁB
����@�����܂ȂԂ̋C�����A�搶�͂��ꂵ���Ȃ��B����ƍK���Ȃ��Ƃɐ搶�̂����Ă��邱�Ƃ́A�܂ȂԂ̎咣�Ƃ͈Ⴄ�B�����̏ؖ��ɏ�@����(��������)�Ƃ����P�������s���Ȃ悤�ɁA�s�����̏ؖ��ɂ��L����Εs�����̗��p�͕K�v�Ȃ��̂ȂB
���܂Ȃԁ��搶�A�Ђǂ��B���ǁA�搶�͉������������̂ł����B
����@���������E���敽�ς͑f���炵���W�����ǁA����������킷���Εs����������Ƃ������Ƃ��B
���悵�����Ƃ������Ƃ͂�����g�������̖���������Ƃ������Ƃł��傤���B����͂ǂ�ȕs�����Ȃ�ł����B
����@�����݂�Ȃ̂悭�����Ă���s��������B
���܂Ȃԁ��c�c���Ԃ�A������ăR�[�V�[�̕s�����ł���B
����@����������A�Ȃ�ŕ��������̂��낤�B
���܂Ȃԁ��搶�ƋC�������ʂ��Ă���Ă������ł���B�ȑO�A�搶���R�[�V�[�̕s�����͑厖�����Ă����Ă����B
���悵�����R�[�V�[�̕s�������āA�m���A
�@�@�@(a2+b2)(x2+y2)��(ax+by)2�@ �@�@���������́Aa�Fb=x�Fy
�Ƃ����s�����ł�����ˁB����ƁA�����̖��̕s�������ǂ����т���ł����B
����@��������̕s�����ɂ́A�����Ƃ��� a��0�Cb��0�Ƃ����̂�����ˁB�Q�������Ƃ������Ƃ��瑊���E���敽�ς̊W�Ɍ��ѕt���Ă��������ǁA���Ƃ������Ƃ́A�������Ƃ��Ƃ������Ƃł�����B�Ⴆ��(3)�̍��ӂ�
�@�@�@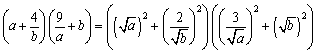
�Ƃ݂Ă����B
�������q�������A�R�[�V�[�̕s�����̍��ӂ̌`�ɂȂ��Ă��B
���܂Ȃԁ��{�����B��������ƁA
�@�@�@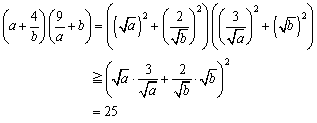
�@���킠���A�ȒP�ɂł���������B
����@�����ł́A���������̏����͂ǂ��Ȃ邾�낤�B
���悵�����䂪������������̂ł�����ˁB
�@�@�@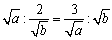
����Aab=6 �ł��ˁB
�������q���搶�A���̖��ɂ��Ă��m�F���Ă����ł����B(2)�́A
�@�@�@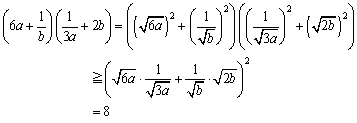
�ŁA���������́A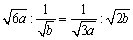 ���A6ab=1 �̂Ƃ��ł��B
���A6ab=1 �̂Ƃ��ł��B
�@����(1)�ł����c�c�A������A������Ȃ��B����͂ǂ�����ł����B
����@�����܂��A���̎��ɂ��Ă̓R�[�V�[�̕s�������g���܂ł��Ȃ���������Ȃ�����ǁA�����ďؖ�����Ȃ�A�s�����̗��ӂ����ł��邱�Ƃ��A���ӂ����������ؖ�����B
�@�@�@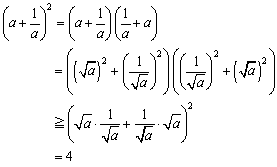
�ƂȂ�B�ǂ����낤�A�������낤�B���̂悤�ɁA�����E���敽�ς̊W�𗘗p�������́A�R�[�V�[�̕s�������g���ĉ������Ƃ��\�ȂB
���܂Ȃԁ��搶���R�[�V�[�̕s�����̐M��҂����Ă��Ƃ͕����������ǁA�Ō�̕s�����͂���ς薳��������Ǝv�����ǁB������ւ�̗Z�ʐ��̈Ⴂ���A�S��A���݂��C�������ʂ������Ȃ������Ȃ�ˁB
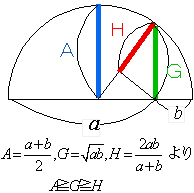 �@����ɂ����鑊���E���敽�ς̊W�̈����́A�����Ԃ�Ƃ���ق₳��Ă��܂��B
�@����ɂ����鑊���E���敽�ς̊W�̈����́A�����Ԃ�Ƃ���ق₳��Ă��܂��B
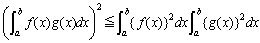
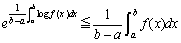
 �@�R�[�V�[�̕s�����قǍő�E�ŏ������n�߂Ƃ��đ���̕���Ŋ���̂ɗ������Ă���s�����͂Ȃ���������܂���B
�@�R�[�V�[�̕s�����قǍő�E�ŏ������n�߂Ƃ��đ���̕���Ŋ���̂ɗ������Ă���s�����͂Ȃ���������܂���B
|
ex) a��0�Cb��0�Cc��0�Cd��0�̂Ƃ��A���̕s�������ؖ�����B �@(1) (a+b)(b+c)(c+a)��8abc �@(2) (a+b)(b+c)(c+d)(d+a)��16abcd |
�@(1),(2)�Ƃ��A�����E���敽�ς̊W���獚���������s�����ł��B
�@������g��Ȃ��ŕs�������ؖ����悤�Ƃ���ƁA�{���ł܂ȂԂ������Ă���悤�ɍ��ӂ���E�ӂ������ĕ����������邵���Ȃ����ƂɂȂ�܂����A����͋ɂ߂č���ȍ�Ƃł��B
�@����������A���ӂ� �̂��ꂼ��ɒ��ڂ����ꍇ�ɂQ�����ł��邱�ƁA���������̃P�[�X���Aa=b=c=d �ł��邱�Ƃ���A����������\�z����ƁA
�@(1) (a+b)(b+c)(c+a)-8abc=c(a-b)2+a(b-c)2+b(c-a)2
�@(2) (a+b)(b+c)(c+d)(d+a)-16abc=ab(c-d)2+ac(b-d)2+ad(b-c)2+bc(a-d)2+bd(a-c)2+cd(a-b)2+(ac-bd)2
�Ƒ�ςȌ��ʂɂȂ��Ă��܂��܂��B�������A����Ƃē��������̏ꍇ���A�����E���敽�ς̊W����ǂ݂Ƃ��āA�ό`���Ă���킯�ŁA��͂葊���E���敽�ς̉��b�ɗa�����Ă���̂ł��B
�@�ł́A������R�[�V�[�̕s�����𗘗p���ďؖ����邱�Ƃ͉\�Ȃ̂ł��傤���B
�@�R�[�V�[�̕s�����́A�Q�������̐ς̊W��\���s�����ł����炱�̖��̂悤�ɁA�R�������A�S�������ɂȂ�Ɗ�{�I�ɂ͎g�����Ƃ��ł��܂���B�����ŁA�e�����Q���̐ςɕό`���鏀�����K�v�ɂȂ��Ă��܂��B
(1)�̏ؖ�)
�@�@�@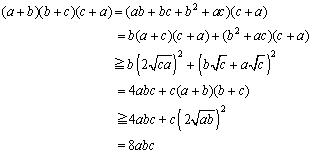
�@���������́Aa2=c2�Cb2=ac ���Aa=b=c
(2)�̏ؖ�)
�@�@�@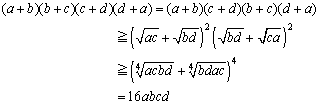
�@���������́Aad=bc�Cab=dc�Cac=bd ���Aa=b=c=d
�@��q�̏ؖ����݂Ă��킩��悤�ɁA(2)�̕����N�₩�ɏؖ��ł��Ă��܂��B����ɂ͗��R������܂��B������������O�ɁA���̖��������Ă݂܂��傤�B
|
ex)�@ �̂Ƃ��A���̕s�������R�[�V�[�̕s�������g���ďؖ�����B �@(1) 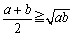 �@(2) 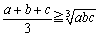 �@(3) 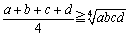 |
(1)�̏ؖ�
�@�@�@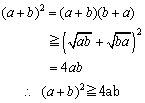
(2)�̏ؖ�
�@�@�@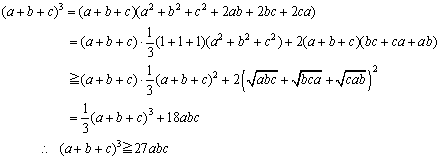
(3)�̏ؖ�
�@�@�@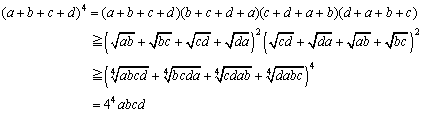
�@���̂悤�ɏؖ����Ă����ƁA��ʂ� 2m�̑����E���敽�ς̊W�ɂ��ẮA�R�[�V�[�E�V�������c�̕s�����𗘗p���ėe�Ղɏؖ��ł��邱�Ƃ�������Ǝv���܂��B23 �ɂ��ẮA
�@�@�@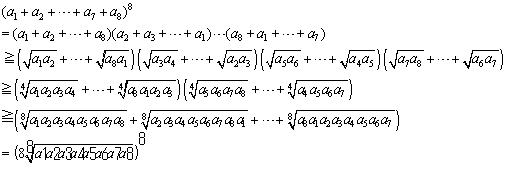
�ƂȂ�܂��B�ȉ� n=2m �̏ꍇ���A�T�C�N���b�N�ɏ����A�R�[�V�[�̕s�������J��Ԃ��Ă��������̂ł��B
�@�Ƃ���ŁA�����E���敽�ς̕s����
�@�@�@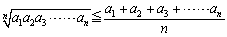
�́A��ʂɂ́An=2m �̏ꍇ���ؖ��ł���ΔC�ӂ� n �̏ꍇ�Ɋg���ł��܂��B
�@�Ⴆ�A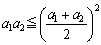 �𗘗p���āA
�𗘗p���āA
�@�@�@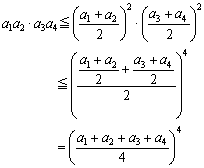
�@�ȉ��A�����Ă����ƁAn=2m �̏ꍇ���A�[�I�ɏؖ�����܂��B
�@�ł́A���̌��ʂ𗘗p���āA�C�ӂ�n�ɂ��āA�ؖ����Ă݂܂��傤�B
�@�@�@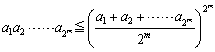
�Ƃ��܂��B�����ŁAn=2m-p��2m-1 �ƂȂ�p���Ƃ�ƁAn+p=2m ���A
�@�@�@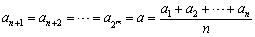
�Ƃ����ƁA
�@�@�@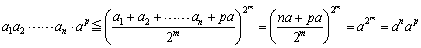
�@�@�@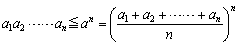
�@����āA�����E���敽�ς̊W���ؖ�����܂����B
�@�R�[�V�[�̕s�����𗘗p���������E���敽�ς̊W�̏ؖ��́An=2m �̏ꍇ�ɂ��ẮA���̏ؖ��ߒ��́A��q�̈�ʓI�����E���敽�ς̏ؖ��ɋ��ʂ��Ă��܂��B�����Ă��̌��ʂ���C�ӂ� n �ɑ��ĕs�������ؖ��ł���킯�ł�����A�R�[�V�[�̕s�����́A�����E���敽�ς̊W���܂�ł���Ƃ�����̂ł��B�{�����A�܂ȂԂ��u����������v�Ƃ������R�[�V�[�̕s�����𗘗p�����ؖ��������A���́A�{���Ɋւ�������̂ł������킯�ł��B
�@�ȏ�̂��Ƃ��A�����E���敽�ςŏؖ�����邷�ׂĂ̕s�����A���邢�͖��́A�R�[�V�[�̕s�����ł��������Ƃ��ł��邱�Ƃ�������܂��B
�@�R�[�V�[�̕s��������� n=2m �ɂ�����ؖ��𗘗p���Ĉ�ʉ��ł���s�����������ЂƂЉ�܂��傤�B
ex) a��0�Cb��0�Cc��0 �̂Ƃ��A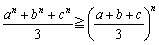 �@(n�́An��2 �ł��鎩�R��) �@(n�́An��2 �ł��鎩�R��)
|
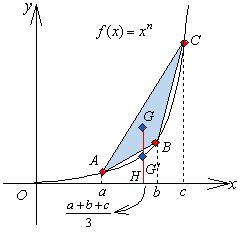 �@���̕s�����̏ؖ��́A�ʊ��̐������狁�߂邱�Ƃ��ł��܂��Bf(x)=xn�Ƃ����ƁA
�@���̕s�����̏ؖ��́A�ʊ��̐������狁�߂邱�Ƃ��ł��܂��Bf(x)=xn�Ƃ����ƁA
�@�@�@f '(x)=nxn-1�C�@�@f "(x)=n(x-1)xn-2
�@����āAx��0 �̂Ƃ��Af "(x)��0 �ł�����Af(x) �͉��ɓʂ̊��ƂȂ�܂��B
�@�قȂ�R�_�� A(a�Can)�CB(b�Cbn)�CC(c�Ccn)�Ƃ��܂��B
�@�O�p�`ABC �̏d�S�̍��W�́A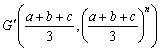 �B
�B
�@�܂��AG ����x���ɉ��낵�������ƋȐ� y=f(x)�Ƃ̌�_��G '�Ƃ���ƁA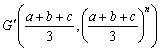 �B
�B
�@�����ŁA���ɓʂ̊��̐������AHG '��HG (�E�})�ƂȂ�܂�����A���_�������܂��B
�@�܂��A���������́A�R�_ A�CB�CC���������Ƃ��A���Ȃ킿�Aa=b=c �̂Ƃ��ł��邱�Ƃ������ł��B
�@�ł́A���ɃR�[�V�[�̕s�������g���ďؖ����Ă݂܂��傤�B
�@�܂��A�������� n �ɂ��āA�ؖ����܂��B
n=2 �̂Ƃ��́A
�@�@�@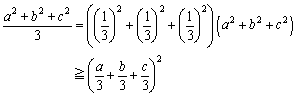
n=3�̂Ƃ��́A
�@�@�@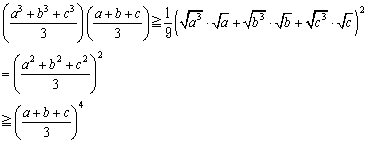
�@������A
�@�@�@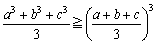
n=4�̂Ƃ��́A
�@�@�@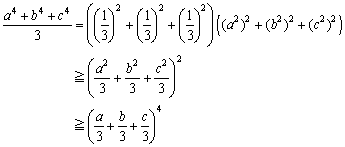
�@���̂悤�ɍl���Ă����ƁAn=2m �̏ꍇ�ɂ��Ă͋A�[�I�ɏؖ��ł��邱�Ƃ�������܂��B
�@�@�@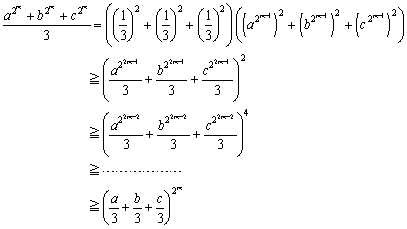
�@���ɁA��ʂ�n�ɂ��āA�������邱�Ƃ��ؖ����܂��傤�B
�@�����ŁA���̂悤�ȏؖ��@���l���܂��B
| ���� P(n)���^����ꂽ�Ƃ��AP(k) ���^�ł���A����P(k-1)���^�ł���A���ׂĂ�n�ɂ��Ė���͐^�ł���B |
�@���̏ؖ��@��ʏ�̐��w�I�A�[�@(forward-induction)�ɑ��āAbackward-induction�Ƃ����܂��B
�@�O�q�̂悤�ɁA���ł�n=2m �ɂ��Ă͏ؖ��ł��Ă��܂�����An-1=2m-1 �ɂ��ďؖ���������킯�ł��B
�@�@�@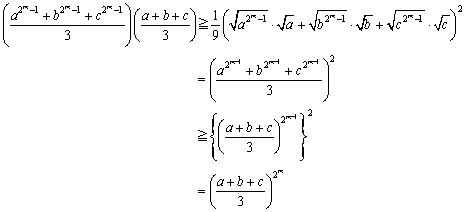
�@�@�@���@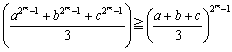
�@����āA���ׂĂ̎��R��n�Ő������܂��B
�@�Ō�ɁA�R�[�V�[�̕s�����𗘗p���āA���K���������Ă݂܂��傤�B
|
ex1) a��0�Cb��0�Cc��0�̂Ƃ��A���̕s�������ؖ�����B �@�@�@ 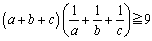
|
�ؖ�)�@�R�[�V�[�̕s�������A
�@�@�@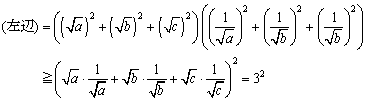
�@���������́A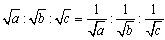 ���Aa=b=c �̂Ƃ��ł���B
���Aa=b=c �̂Ƃ��ł���B
|
ex2) a��0�Cb��0�Cm��0�Cn��0 �Ƃ���B���̕s�������ؖ�����B �@�@�@m+n=1�̂Ƃ��A 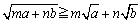
|
�ؖ�) �R�[�V�[�̕s�������A
�@�@�@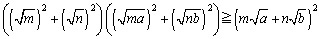
�@�@�@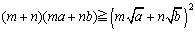
�@m+n=1���A
�@�����ŁAma+nb��0 �A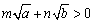 �ł��邩��A
�ł��邩��A
�@�@�@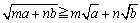
�@���������́A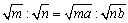 ���Aa=b�̂Ƃ��ł���B
���Aa=b�̂Ƃ��ł���B
| ex3) x+y+z��3 �̂Ƃ��Ax2+y2+z2��x+y+z���ؖ�����B |
�ؖ�) �R�[�V�[�̕s�������A
�@�@�@