

<先 生>
|
ex) 男6人、女4人の合わせて10人の生徒について、次の場合の数を求めよ。 (1) 4人を選ぶとき、少なくとも1人女子が含まれるような選び方は何通りか。 (2) 5人ずつの2つのグループに分けるとき、特定の2人が別々のグループになるような分け方は何通 りか。 |
○本質をスリムいてみよう!
<先 生>
<よしお>
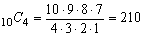
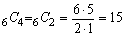
<先 生>
<かず子>
<先 生>
<まなぶ>
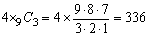
<かず子>
<先 生>
<よしお>
<先 生>
<生徒達>
<かずお>
<先 生>
| 男3人、女2人の5人の中から2人選ぶとき、少なくとも1人女子が含まれる場合の数を求めよ。 |
<よしお>
<先 生>
<かず子>
<先 生>
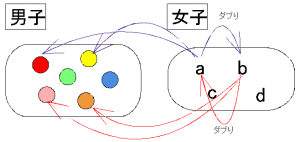
<かず子>
<先 生>
<かず子>
<先 生>
<かず子>
<先 生>
○リーダーはだ〜れ?
<先 生>
<まなぶ>
<よしお>
<まなぶ>
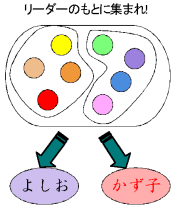 <かず子>
<かず子>
<先 生>
<まなぶ>
<かず子>
<先 生>
<まなぶ>
<先 生>
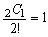
<かず子>
<まなぶ>
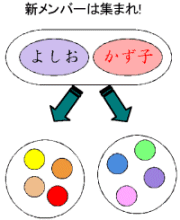 <先 生>
<先 生>
<まなぶ>
<先 生>
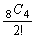
<まなぶ>
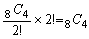
<先 生>
<まなぶ>
<かず子>
あとがき
さて、その研究会の後、興奮冷めやらぬ余韻を残して、数学好きのおじさん達が誰誘うともなく集まって寄った居酒屋ででた話題が今回の組合せの小手技です。発端は、
「昔は場合の数を求めるときには重複なく数えるっていうのが教科書に必ず載っていたけど、最近はないよなあ」フランクな人と人との付き合い。数実研の原点がここにあります。
「そうそう、そういえば生徒からこんな質問でたんだけど、どう思う」 ………………………………………………………………………………