

| ex1) z1=1+3i,z2=a+i,z3=3+5iを表す3点をA,B,Cとするとき,3点が一直線上にあるようにaの値を求めよ. |
<まなぶ>俺,これ大嫌いなんだよな.
<よしお>どうして?
<まなぶ>だってさ,これベクトルの問題では凄い簡単にできるじゃん.だけど,複素数でやろうとすると,分数の形にして,なんか実数になるだとか純虚数になるだとかわけの分らないことをやるだろう.わざわざ問題を難しくして僕らを苛めているようにしか思えないだろ.
<かず子>ちょっと被害妄想という気もするけど,言われてみればそうよね.
<先 生>公式を確認してみようか.
複素数平面上の異なる3点P(z1) ,Q(z2) ,R(z3)について,
① 3点P,Q,Rが一直線上 ⇔ 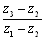 は実数 は実数② PQ,QRが直交 ⇔ 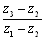 は純虚数 は純虚数
|
<まなぶ>そうそう,これこれ.
<かず子>まなぶは乗り気じゃないみたいだから,私が計算してみます.①の一直線上の場合の問題だから,
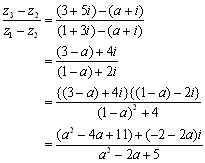
これが,実数になることより,
-2-2a=0 ∴a=-1
ほんとうに,面倒だわ.
<よしお>かず子は,公式にそのまま代入してしまったから計算が面倒になったけど,この場合のz1,z3は確定している複素数だから,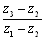 で計算すると多少は楽になると思うよ.でも,確かにベクトルによる方法に較べると大変だね.
で計算すると多少は楽になると思うよ.でも,確かにベクトルによる方法に較べると大変だね.
<まなぶ>でしょう,でしょう.みんなもそう思うだろ.でもベクトルでは,3つの点をA(1,3) ,B(a,1) ,C(3,5)と同一視することで,3点A,B,Cが同一直線上にあるための条件は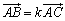 なんだから,
なんだから,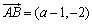 ,
,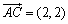 より,
より,
(a-1,-2)=k(2,2)
これから成分を比較すると,
a-1=2k,-2=2k
∴ a=-1
ほら,簡単にできた.
<先 生>今日の授業で先生が言いたかったことをみんなまなぶがいってくれたね.先生もこの問題はベクトル的に処理すべきだと思うんだ.
<かず子>へぇー,先生がまなぶを評価するなんて珍しい.
<まなぶ>かず子,まだまだ甘いな.残念ながら,先生の性格に僕は裏切られたことはないよ.先生はいま,「ベクトル的」といったわけで,僕がやったように「ベクトル」で解くべきだといっているわけではないよ.図星でしょ.
<先 生>おほん!.まなぶくんも,ずいぶん大人になったね.でもその通り.せっかく複素数分野を学習しているんだから複素数で考えてみよう.大事なことはね.この分野は図形の性質を調べるために複素数を利用しているんだってこと.それが道具が変われば,座標平面に置き換えたり,ベクトルや,三角比を使ったりすることになる.でも,もともとは初等幾何での条件がベースになっているわけで,この場合は,その条件はAB=kACであることは明らかだろう.それをさきほどまなぶはこの条件をベクトルで表したわけだ.では複素数で表すとどうなるだろうか.
<よしお>複素数平面上では基準は原点に考えるから,3点がO(0) ,A(α) ,B(β)である場合は,
β=kα(kは実数)
となることですよね.
<先 生>その通り.だから,3点をA(z1) ,B(z2),C(z3)として,必ずしも原点でない場合には,例えばAを原点に平行移動してしまえばよい.このときB,Cは,z2-z1,z3-z1に移るから,
z2-z1=k(z3-z1)
となる.そうすると,exの場合はどんな条件になるだろう.
<かず子> z2-z1=(a+i)-(1+3i)=(a-1)-2i
z3-z1=(3+5i)-(1+3i)=2+2i
これから,(a-1)-2i=k(2+2i)
だから,実部と虚部を比較すると,a=-1.
あれ?,この解法,なんかベクトルと同じだわ.
<よしお>それで,ベクトル的って先生はいったんですね.
<先 生>そう,ベクトルを成分表示したとき,x成分を複素数の実部,y成分を虚部に対応させれば複素数はベクトルと見なすことが可能となり,ベクトルと同じように処理することができる.では,垂直になる場合はどういう条件になるだろうか.
| ex2) 前問ex1の3点A,B,Cにおいて,ABとACが垂直となるとき,aの値を求めよ. |
まず,3点をO(0) ,A(α) ,B(β)とし,原点を中心とみて,αを何度回転させればβになるか考えてみよう.
<まなぶ>そりゃ,直角なんだから,90°でしょ.
<かず子>-90°って場合もあると思うわ.
<先 生>そうだね.複素数において積は,原点を中心とした回転を表すわけだから,結局,
β=±iα
としていいことになるね.
<よしお>あっ,先生,それおかしいと思います.90°回転してもαとβの大きさが等しいとは限らないのではないですか.
<先 生>正解.先生の引っ掛けにはまらなかったね.正確には,複素数の積は回転と拡大・縮小を表している.
したがって±90°回転し,さらに大きさが定数倍されることも考慮すると,
β=kiα (kは実数)
とすればいいことになる.これを利用して例題を解いてごらん.
<まなぶ>まず,点Aを原点に移動させて,回転の中心にします.そうすると
z2-z1=ki(z3-z1)
これから,
(a-1)-2i=ki(2+2i)=-2k+2ki
より,実部・虚部を比較して,
k=-1,a=3
となります.
<先 生>もちろんベクトルで考えると,この問題は,内積という常套手段を使うともっと簡単にできるけど,複素数の垂直条件も分数で計算するよりは回転とみなすことで簡単に計算できることが分ると思う.
さて,ところで,みんなは点Aを原点に移すことで,他の点も移動させたわけだけど,このことはベクトル的に考えると何を意味するのだろうか.
<かず子>点Aを原点にしたということだから……,分った,点Aを位置ベクトルの始点とみなすということでしょ.
<よしお>なるほど.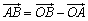 と変形することと同じなんですね.
と変形することと同じなんですね.
<先 生>その通り.複素数は原点を中心とする変換であるわけだから,任意の点を中心として変換を考えるにはその点を位置ベクトルの始点とみればいいということになるんだ.このように,複素数はベクトル的に見ることができることになるけど,そうするとだ,複素数にあって,ベクトルにない演算は必要ないと考えられないだろうか.
<まなぶ>それって「割り算」のことでしょ.そうか,先生も割り算は嫌いなんだ.
<先 生>嫌いというわけではないが,必要ないのではといっている.
<かず子>でも先生,割り算ができるからこそベクトルを使うよりもいろいろな図形の性質が複素数では導けるのではないでしょうか.
<先 生>割り算は,掛け算の逆演算に過ぎない.複素数がベクトルと違うことは,点や図形を回転,伸縮させることができるということであり,それは,割り算というよりむしろ掛け算から言えることだ.
具体的にいうと,
w=αz
とは,
「wはzを,原点を中心として,|α|倍し,arg α回転した点」
であるということだ.これを回転の中心をz1にするならば位置ベクトル化して,
w-z1=α(z-z1)
となる.この式の両辺をz-z1で割って教科書にあるような公式を作ることにはあまり意味のないことではないだろうか.たとえば,次の問題
ex3)複素数平面上の3点A(z1) ,B(z2) ,C(z3)が,関係式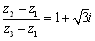 を満たすとき,三角形のABCの形状を求めよ. |
 <よしお>これは,両辺の偏角と絶対値をとって……
<よしお>これは,両辺の偏角と絶対値をとって……
<先 生>ストップ.そういうように考えるべきではなくて,両辺に(z3-z1)を掛けて分母を払ってごらん.
<よしお>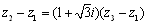 となります.あっ,そうか.先ほど先生がまとめたことを考えると,これは点z1を中心として,点z2は点z1を,
となります.あっ,そうか.先ほど先生がまとめたことを考えると,これは点z1を中心として,点z2は点z1を,
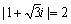 倍
倍
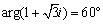 回転
回転
した点ということですね.
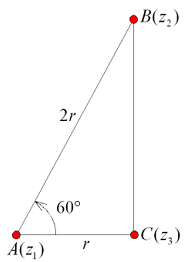
<先 生>それを図に書くと,右図の正三角形を半分に切った形になる.変換の過程がすっきりみえてくるだろう.
では,同じように考えると,次の問題はどうすればいい.
| ex4) 複素数平面上の異なる3点O(0),A(α),B(β)が,α2-αβ+β2=0を満たすとき,三角形△OABはどのような三角形か. |
<かず子>普通は,与式の両辺をαで割って,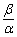 を求めるんでしょ.
を求めるんでしょ.
<まなぶ>でも先生は割り算は考えないっていってるんだから,このまま2次方程式を解くんじゃないのかな.ということは,αかβの2次方程式とみることになりますよね.
<先 生>どっちにする.
<まなぶ>やだな,なんか験されているような気がする.じゃあ,αの式とみると,
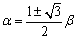
となるから,あっ,分った.これは原点を中心としてβをαに変換したということですね.
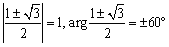
だから,△OABは正三角形ですね.
確かにこう考えていくと,割り算なんて必要ないように思えますね.
<先 生>却って,割り算をすることで,変換の仕組みが却って見えにくくなっているように思えるだろう.
にも関わらず複素数には何故か割り算に固執した問題が多い.例えば,
ex5) 複素数平面上の5点O(0),E(1) ,P(z1) ,Q(z2) ,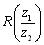 に対して,△OEQ∽△ORPであることを証明せよ. に対して,△OEQ∽△ORPであることを証明せよ.
|
さて,相似であることをどうやって示すかということだけど,複素数の積が変換であるということを考えてみれば,すぐに結論がでる.
△OEQについてみると,原点を中心として,Q(z2)はE(1)をどのように変換したかは,
z2=z2・1
とみれば,|z2|倍し,arg z2回転したことが分る.では同じように考えると,原点を中心としP(z1)は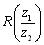 をどのように変換した点だろうか.
をどのように変換した点だろうか.
<よしお> はい,
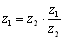
ですから,変換を表す複素数はz2となります……,あっ,これは点Eから点Qの変換と同じですね.
<先 生>そう,したがって2つの三角形の2辺は同じ複素数で変換されているわけだから相似となるのは明らかである.しかし,これを割り算とか絶対値をとって技巧的に解法を導く方法があるけど,結局は変換の本質を見失うことになってしまう.
では,もう1題.次の問題はどうだろう.
|
ex6)点P(z)が単位円周上の点であるとき,次の等式を満たす点wはどんな図形を描くか. (1) w=(1-i)(z+1) (2) 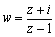
|
<よしお>点P(z)が単位円周上の点であるということは
|z|=1
と表されるということですね.したがって,等式をzについて解いて,この単位円に代入すればwの関係式が作れます.
<まなぶ>そうすると(1)は,
w=z+1-iz-iより,
z(i-i)=w-1+i
この両辺を(1-i)で割って…
<先 生>ストップ!
<まなぶ>……先生,心臓に良くないよ.食いかけの食べ物が喉に詰まってしまうような止め方.
<先 生>品のない例えだな.まなぶはいま割り算をしようとしただろ.今日のテーマはベクトル的に考えて割り算を使わないでどう求めたらいいかということだ.もっと細かなことをいうと,展開そのものも要領がよくない.
この場合は1-iをひとつの複素数と考えて,
w=(1-i)z+(1-i)
これから, w-(1-i)=(1-i)z
となる.
<まなぶ>でも,先生,最終的な変形の結果は同じですよ.
<先 生>このあとが問題なんだ.zについて単位円に代入すると考えるのではなく,この式の両辺の大きさを考えてごらん.
|w-(1-i)|=|(1-i)z|=|1-i||z|=2
となるだろう.そうするとこの軌跡は何を意味する.
<かず子>中心が1-iで半径2の円ですね.ほんと.見方を変えただけで随分簡単になったような気がする.
<よしお>結局,僕が最初にいった|z|=1に代入するってことがまずかったんですね.じゃあ,汚名挽回で(2)をやってみます.
分母を払って
w(z-1)=z+i
左辺にzを集めて,
z(w-1)=w+i
両辺の大きさを求めて
|z||w-1|=|w+1|
|z|=1であるから,
|w-1|=|w+i|
よって,A(1),B(-i)とすると,求める軌跡は,ABの垂直二等分線となります.
<先 生>だいぶ,ベクトル的計算に慣れてきたね.割り算をするということは,
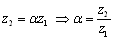
だから,変換を表している複素数αをむき出しにするってことだ.そうすることで,マニュアル的に大きさと偏角は求められるが,変換元のz1と変換先のz2の複素数が見づらくなってしまうんだ.
複素数の変換は「何を何で変換して何になるか」っていうことをしっかり見据えて考えるべきだろう.まあ,いってみれば,君たち3人の関係みたいなものだな.
<まなぶ>ん?割り算が必要ないってことは分ったけど,先生は僕たち3人が,それぞれどんな複素数を表しているって思っているんですか.
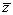 (共役複素数)による変形
(共役複素数)による変形
| ex)A(2,1) ,B(4,3)とするとき,△ABCが正三角形となるように,頂点Cの座標を求めよ. |
この問題を直交座標平面で解こうとするとてこずりますが,与えられている点を複素数平面という架空(異次元)の平面に飛ばしてしまうと,途端見通しがよくなります.A,Bは,それぞれ複素数2+i,4+3iに対応し,2+iを中心として,60°回転した点が複素数平面での点Cとなります.
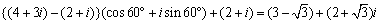
こうやって求めた点Cを最後にリアルワールドである直交座標に戻して,
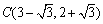
が求める頂点となります(△ACBと考えた場合は-60°回転もありますが).
このように現実の世界では困難な作業を,バーチャルな世界で解析することに複素数の味わいがあるわけです.それを①のように,複素数平面での議論を避けて,いきなり現実に戻してしまうことは,例えれば,寝ていて心地よい夢を見ていた子供を叩き起こして,散々説教をした挙句,早く寝なさいといって追い立てているようなものです.複素数平面の面白さを指導しようとするならば,①の方法は極力避けたいものです.
②は,複素数の実部と虚部を抽出するものです.
実部 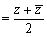 ,虚部
,虚部 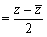
となります.また,複素数の大きさは,
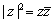
から得られますが,これは,ベクトルにおける
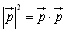
と同様に軌跡問題に威力を発揮します.ただ,この方法は,バーチャルの世界から現実の世界を見下ろして議論するようなもので,間接的にはデカルト座標での仕事をしていることになります.その煮え切らないスタンスは見方によっては①以上に始末に置けないといえるかもしれません.
対して③はもっとも複素数の性質を反映するものです.図形問題は,詰まるところ,初等幾何のアイデア(補助線)的アプローチで解決されますが,そのアイデアをバイパスする方法(道具)が,座標平面,ベクトル,複素数であるかと思います.真っ白なノートに描かれた図形を,直交座標平面,斜交座標平面,ガウス平面といった平面に置き換えて図形の性質を調べるわけです.図形を直交座標では真っ直ぐ見下ろし,斜交座標では斜めに見て,そしてガウス平面では並行次元にテレポートさせるわけです.世界が変容することにより,使用する道具立ても変化します.距離や分点の公式はそれぞれ
|
【直交座標平面】 A(x1,y1),B(x2,y2) とするとき, ① 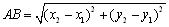 ② AP:PB=m:nなる点P(x,y)は, 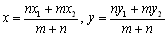 |
【斜交座標平面】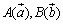 とするとき, とするとき,① 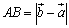 ② AP:PB=m:nなる点 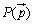 は, は,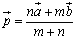
|
|
【複素数平面】 A(α),B(β)とするとき, ① AB=|β-α| ② AP:PB=m:nなる点P(z)は, 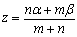
|
と表され,同じように表現されます.したがって,この3つの平面の決定的違いは,これ以外の道具の使用によることが分ります.その道具を③として,次のように考えて見ましょう.
|
【直交座標平面】 ③点A(x1,y1)と直線ax+by+c=0との距離dは, 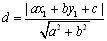
|
|
【斜交座標平面】 ③ 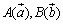 のなす角をθとすると, のなす角をθとすると,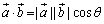
|
|
【複素数平面】 ③β=ωα ⇔ 点B(β)は点A(α)を,原点を中心に|ω|倍,arg ω回転したものである. |
それぞれ,ヘッセの標準形,内積,極形式に関するものです.ベクトルと複素数平面の場合はどちらも積から角度を求めるものです.複素数では,
|
【複素数平面】 ③A(α),B(β)のなす角をθとすると, 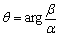
|
とみなせばいいわけですが,複素数の積における伸縮条件がこれでは省かれてしまいます.
直交座標平面では2点A,Bに対して,∠AOB=θを求めることもできます.2直線y=mx,y=nxのなす角θは,
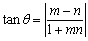
で与えられます.ここで,A(x1,y1),B(x2,y2)とすると,OAとOBのなす角は,
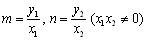
であることより,
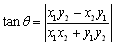
で得られます.ただ,これを直交座標平面での③の公式とみなすには実にゴツいし活用範囲に乏しいといえます.
では,前述の3つの平面での道具③に共通することはというと,実は△OABの面積を求めることができるということです.三角形の各辺の長さは道具①で求められます.したがって,直交座標平面では③は,三角形の高さから面積が得られ,
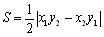
となることは周知のことです.
また,斜交座標平面では,道具③で得られた余弦の値から,
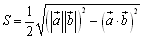
となります.あるいは,外積という積を導入すると,
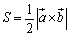
という綺麗な結論が得られます.
では,ガウス平面③においてはどうなるでしょうか.
OA,OBのなす角をθとすれは,
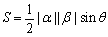
β=wαとすると,
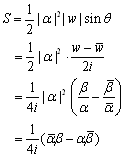
ここで,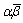 は
は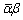 の共役複素数であるから,
の共役複素数であるから,
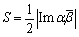
なるシンプルな結論が得られます.
| ex)α=3+5i,β=2-4iのとき,三角形0αβの面積を求めよ. |
解)
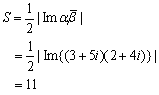
初等幾何がgeo-metry(土地を測る=測量)として発展し,その道具として3つの平面が考え出されたのであれば,土地を測る最大の関心事である土地の面積を求めることは至極当然のことであるといえるでしょう.それぞれの平面での道具③は,面積を求めるためのエッセンスを導く道具であると考えるのが自然なのです.
ところで先ほど求めた複素数平面での面積公式は,
α=x1+y1i,β=x2+y2i
とすれば,
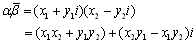
より,この虚部をみることで,直交座標での面積公式から複素数平面での公式が確認できます
(ちなみに実部はベクトルの内積であり,虚部は外積×2であり,3つの平面がミスマッチしています).
このように,baseに幾何(平面図形)がある以上はその解法は一つの平面に置き換えることで固執されて解かれるべきではないでしょう.
面積については,直交座標で求めるのがやはり一番簡単なのです.線分の直交条件についてはベクトルの内積に勝るものはありません.そして,点や図形の回転は,複素数平面の独擅場です.このようにそれぞれの持ち場が最大限活かせるように,その扱いについても注意したいものです.
複素数平面は,存在しない数を存在させたことにより,より図形の存在を大きくすることに成功しました.その手口はまるで魔法をみるようなもので,変換は変身でもあるのです.かぼちゃが馬車に化けることはありませんが,それでも図形が回転することは,たまげたことなのです.流体力学のように,現実世界に活躍の場を見出すことになるのは当然のことといえるでしょう.
しかし,その複素数平面もいよいよ次年度を最後に高校数学から姿を消します(入試まで考えてもあと2年です).行列の代替分野として登場した複素数平面が消えることは,回転というアニメーション的なイメージを喚起する分野がなくなることを意味します.高校数学からまた,想像することがなくなろうとしています.
最後に本文の結びで先生は,まなぶ,かず子,よしおの3人を,変換(operator),変換元,変換先の複素数に例えています.この中で,もちろんoperator的存在は,まなぶとかず子の仲立ちとしてのよしおであることに依存はないでしょう.
では,まなぶとかず子のどちらが変換元になるでしょうか.俗っぽい言い方をすれば,どちらが数学の話題を通して相手にすり寄っていくかということで,この現実世界におけるcomplex-relationは,まだまだ波乱含みの展開を平成15年度には見せそうです.