

○効率的な式の整理法について
<先 生>今日は、複素数平面上の点P(z)が、
![]()
を満たすとき、点Pの軌跡を求めてみよう。
まず、式の整理からだ。S君、どうすればいい。
<生徒S>えーと、文字zについて降べきの順に整理だと思います。だから、
![]() ……(*)
……(*)
<先 生>そうだね。文字式の整理の基本だね。さあ、あとはこの式から軌跡を求めるわけだけど、いままでの学習から軌跡は、たいていは直線か円だったよね。では、この式の場合はどっちだろう。はい、Aさん。
<生徒A>与式に、![]() がありますから、円だと思います。
がありますから、円だと思います。
<先 生>正解! ![]() とおくと、
とおくと、![]() から予想できるね。ところで、複素数では、
から予想できるね。ところで、複素数では、
中心A(α)、半径rの円の方程式は、![]() ie
ie ![]()
で表現できるんだったね。
後は、(*)の左辺をこういった形になるように式変形すればいいわけだ。まっ、要は強引に因数分解するってことだ。
S君やってごらん。
<生徒S> うーん、![]() が、
が、![]() になればいいんだから、
になればいいんだから、
![]()
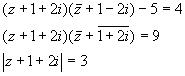
<先 生> 結論、したがって、中心![]() で半径3の円ってことだ。
で半径3の円ってことだ。
だけど、これで確かにこの問題は解けたけど、式変形は随分見苦しいよね。ここら辺のところもう少し上手くできないだろうか?
<生 徒>………
<先 生> ちょっとヒントをだそう。こういった式変形どっかでお目にかかったことないかな。
<生徒B> はい、先生。不定方程式の問題だと思います。
<先 生>そうだね。例えば、
![]() を満たす整数x,yを求めよ。
を満たす整数x,yを求めよ。
と同じだね。この左辺も強引にx,yの一次式の積に分解するのだけれど、肝心なことはどの文字で整理するかということなんだ。
<生徒A> xじゃないんですか?
<先 生> もちろんxでもいいけど、それでは先程と同じ解答になってしまうだろう。式を良く見てごらん。実は、この式、もう既に整理されているんだよ。
<生徒S> あっ、xとyの二文字だ。
<先 生> その通り。xyが2次、4x+2yが1次とみればいいんだ。さあ、そうすると2次式の因数分解といったら、お助け公式のタスキがけがあったね。やってみよう。
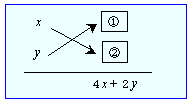
さて、上の①と②にはいる数字はなんだろうか。
<生徒A> ①が2,②が4です。
<先 生> そうだね。よって与式の左辺は、(x+2)(y+4)と変形すればよいことがわかる。あとは定数項の調整だ。①×②=8が左辺の増えた分であるから、右辺にも(=は天秤ばかりの支点と考えよう)増えた分だけ加えて、
(x+2)(y+4)=9
となるわけだ。
ではこれを複素数の軌跡の問題で利用してみよう。どうすればいいかな。
<生徒S> zと![]() に着目。
に着目。
<先 生> そうだね。そうみるとこの式は、与式段階で整理されていることが分かるね。さあ、タスキ掛けだ。
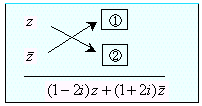
①=1+2i,②=1−2i であることは、簡単にわかるだろう。左辺の増加した値は、
(1+2i)(1−2i)=5
だから、与式を変形すると、(z+1+2i)(z+1−2i)=9となる。
まっ、結局この軌跡の問題は、単純な式変形の問題で、どう効率よく式を変形するかってことなんだ。
何事も、基本が大切ってことだね。
【演 習 】
ex1) x2−xy−2y2−4x−y+3を因数分解せよ。
解) (与式)=(x−2y)(x+y)+(−4x−y)+3より、
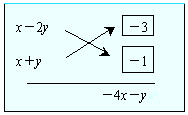
故に (与式)=(x−2y−3)(x+y−1)
ex2) 3xy+2x−y=0を満たす整数x,yを求めよ。
解)
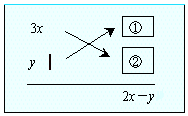
より、①=−1,②=![]() である。ゆえに、
である。ゆえに、![]()
両辺を3倍して、(x−1)(3y+2)=−2
これを満たす整数x,yの組は,(x,y)=(3,−1),(0,0)である。
ex3) ![]() を表わす複素数平面上の点P(z)の軌跡を求めよ。
を表わす複素数平面上の点P(z)の軌跡を求めよ。
解)
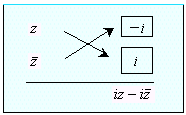
より、![]() ,
, ![]()
故に、中心iで半径2の円。
○大局的図形概念のイメージ法
<先 生> 今日は次の問題について考えてみよう。
|
ex) 異なる3つの複素数、α,β,γの間に、 (1+i)γ+2β=(3+i)α ………(*) なる関係があるとき、3点A(α),B(β),C(γ)を頂点とする三角形ABCの形状を求めよ。 |
さて、複素数平面上の図形の形状を求めるには、偏角と絶対値を利用して、三角形の内角の大きさと、辺の長さを求めればよかったよね。
その為には、頂点の一つを回転の中心にすることが必要だ。
例えば、頂点A(α)を中心(原点)とみて、β−αとγ−αのなす角を求めてみよう。
では、与式をαについて解いてから、β−αとγ−αを計算してごらん。
<生 徒> ![]() だから、
だから、
![]() ………①
………①
![]() ………②
………②
となります。
 <先 生> そうだね。これから、
<先 生> そうだね。これから、
![]()
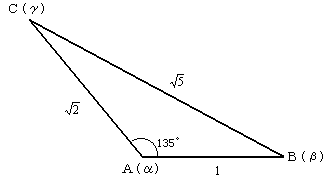
したがって、点Cは、点Bを点Aの周りに135°回転させて、点Aからの距離を![]() 倍したものだということがわかる。
倍したものだということがわかる。
それを図に表わすと、右図の三角形になるわけだ。
ところで、実は、みんなは今、随分無駄な計算をしていたんだ。そのことに、気がついた人はいるかな。
<生 徒> ………
<生徒A> ①の式は、βを回転の中心とした変形式だと思うんですけど。
<先 生> うん。いい線いってる。①から、![]() ………③
………③
同じように考えると、②の式から、![]() ………④
………④
となることも分かるね。これはいったい何を意味するのだろうか。
<生徒S> ……!。先生、③,④の右辺の分子・分母の複素数は、みんな与式のα,β,γの係数になってます。
<先 生> OK!やったね。
さあ、今、S君のいったことをみんなで考えてみよう。
この問題の解答の方針は、点Aを回転の中心にして、
![]()
という形に変形することだったね。
ここで、大事なことは、右辺の複素数zだ。
このzは、回転と拡大(縮小)を表わすけど、α,β,γとは関係のない複素数であるってことなんだ。
すなわち、これから与式は、
γ−α=z(β−α)
と変形できることが問題の中で保証されていなければならないんだ。
そう考えて、与式(*)をみてごらん。……。
うん。今いち理解してないね。具体的に話そう。
例えば、(*)を、点Aを回転の中心として考えてみよう。
左辺のβやγはそれぞれ、
β⇒β−α
γ⇒γ−α
と変形されるけど、このとき、その変形に合わせて右辺のαは相殺され消去されなければならないってことなんだよ。
<生徒C> じゃあ、例えば点Bを回転の中心にすると、左辺のγをγ−β、右辺のαをα−βに変えて、βを消せばいいんだから……
(1+i)(γ−β)=(3+i)(α−β)
あっ、ほんとだ。③と同じになる。
<先 生> 同じように、点Cを回転の中心にすると、
2(β−γ)=(3+i)(α−β)
となることも簡単に分かるね。
だけど、この2つの式からは回転角はでてこないよね。先生が最初に点Aについて解いてごらんといったのは、実は求められる角を初めから予想してたってわけだ。このように、結果を予想しながら、解答を見下ろしてみると、複素数平面の問題は随分見通しが良くなるものなんだよ。
<生徒A> 先生、角度は求められないけど、上の2つの式から倍率(拡大、縮小)は分かりますよね。
<先 生> いいことに気がついたね。2つの式の絶対値をとってみよう。
![]() ∴
∴ ![]()
![]() ∴
∴ ![]()
よって、
![]()
となる。これを答えとしても、もちろんいいね。なんか、法則(公式)が作れそうな気がするね。
<生徒S> 先生、どんな場合でも、こうやってできるんですか。
<先 生> 条件を考えてごらん。
《左辺の係数の和》=《右辺の係数》
となっていればいいことがわかるはずだよ。
まあ、あとは出題者が問題を間違えなければってとこかな。
<生徒S> ……。
【演 習】
ex) 3つの異なる複素数α,β,γの間に、
![]()
なる関係があるとき、3点A(α),B(β),C(γ)を頂点とする三角形はどんな形か。
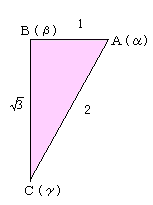
解) 回転の中心を点Bとすると、与式は、
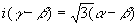 よって、
よって、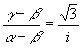
これから、点Cは、点Aを点Bの周りに−90°回転させて、![]() 倍したものだから、
倍したものだから、
A=60°,B=90°の直角三角形。
なお、![]() とみると,
とみると,
![]()
は明らか。