○実を食してから味わうべし

＜先　生＞今日は，判別式の使い方の問題です。

ex) 2つの方程式　 　　　x2+ax+3−a=0･･･�@ 　　　x2＋(3−a)x＋a＝0･･･�A の解が次のようになるとき，実数aの値の範囲を求めよ。 　(1) 少なくとも一方が実数解 　(2) 1つの方程式の解は実数解，他の方程式の解は虚数解

　まずは，方向性をまとめてみよう。

＜かず子＞ (1)は，「少なくとも一方」という慣例句がありますから，「両方とも虚数解」であるaの範囲を求めて，その余事象を考えればいいと思います。(2)は，場合分けです。「�@実数解　�A虚数解」と「�@虚数解　�A実数解」のそれぞれについて求めます。

＜先　生＞まあ，一般的な方向だね。

＜よしお＞まずいんでしょうか？。

＜先　生＞まずくはないよ。でも(1)，(2)と似たような問題が２つあるんだから，出来ればひとまとめして解きたいよね。みんなはね。いつも判別式を使う前に，何かとその解の範囲に捕らわれ過ぎる嫌いがあるね。まずは実数条件を考え，その後に虚数のことは考えればいいんだよ。だって例えば虚数解を求めるのならば，実数解のaの値の範囲がわかっていれば，それ以外を考えればいいわけだから。それでは，�@，�Aの判別式，D₁，D₂を計算してみよう。

＜生徒達＞　D₁＝a²−4(3−a)＝a²＋4a−12＝(a＋6)(a−2)
　　D₂＝(3−a)²−4a＝a²−10a＋9＝(a−1)(a−9)

＜先　生＞では，まなぶ。�@，�Aの解が実数解であるときのaの値の範囲はどうなるだろう。

＜まなぶ＞ D₁≧0，D₂≧0ですから，
　　a≦−6，2≦a
　　a≦1，9≦a
となります。

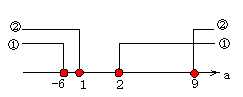＜先　生＞それでは，このaの範囲を数直線上に表現してみよう。
　さあ，図をみてごらん。�@，�Aが実数解を持つ範囲は，数直線の上にある平行な横線で表されているね。この本数を数えれば，実数解の個数が判別できるわけだ。
　例えば，横線が２本ある範囲は，�@も�Aも実数解をもつ範囲という具合だ。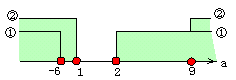

　では，問いをみていこう。まず，(1)の少なくとも一方が実数解ということは，�@，�Aどっちでもいいから，解が実数ってことだ。したがって，横線が「少なくとも１本」あればいいわけだから，その範囲を求めると，
　　a≦1，2≦a
となる。では，よしお，(2)の場合の横線は何本だ。

＜よしお＞片方が実数解のとき，もう片方は虚数解なんだから，「横線が1本」の場合です。

＜先　生＞その通り。では，まなぶ，範囲を求めてみよう。

＜まなぶ＞はい，横線１本のところをなぞって……，
　　−6≦a≦1，2≦a≦9
となります。

＜先　生＞等号の部分はみな含まれるかな。

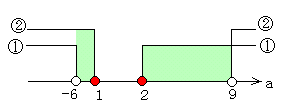＜まなぶ＞a＝−6のときは，�@も�Aも実数範囲に含まれるからダメでした。えーと，他も同じように吟味して，
　　−6≦a≦1，2≦a≦9
　こんどはいいですか。

＜先　生＞ＯKだね！。等号の扱いには注意しよう。では，同じようにこの図を利用すると，例えば，
　　　(3)どちらも虚数解
なんて問題も，即答できるね。

＜よしお＞はい，「横線がない」範囲だから，1＜a＜2です。

＜先　生＞そう，それでいい。では，確認だ。
　判別式は，基本的には実数条件を求めるために使えば充分であるということだ。問題文で虚数解の範囲を要求していても，固執する必要はまったくない。
　まずは，実（み）…実数のことだよ…を食べてから，そのあとにうまい，まずいを味わえばいい。まなぶは食べてみて，味はどうだった。

＜まなぶ＞実数も虚数もどちらとも僕にとっては硬過ぎ(難過ぎ)ます。

＜先　生＞………