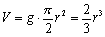

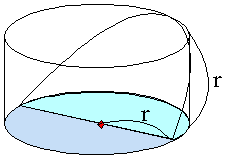
| �@ex) �~�̔��a��r�Ƃ��Đؓ��~���̑̐ς����߂�B |
���悵�������̑卪�łł������̂́A�~�̔��a�ƍ���������������A���a���܂ނ悤�ɁA�S�T߂̊p�x�ŕ�����ꂽ�Ƃ������Ƃł��ˁB
����@���������������Ƃ��ˁB�Ƃ���ł��̖��������O�ɁA������Ƃ����炢���B���̂̑̐ς͂ǂ�����ċ��߂邩�Ƃ����ƁA���̂�K���ȕ����ɃX���C�X���āA���ꂼ��̒f�Ђ̖ʐς����߂�����W�߂�悩������ȁB���Ƃ��A�~�̉~���̒�����N�ւ̂悤�ɑ��₵�Ă����Ɖ~�̖ʐςɂȂ�B�~���Q��r��ϕ�����Ɖ~�̖ʐσ�r2�ƂȂ�Ƃ������Ƃ��B�܂��A���ʂ̕\�ʐςS��r2���`���R�{�[���̕\�ʂɃ`���R���R�[�e�B���O���Ă����悤�ɓh���Ă����ƁA���̑̐� 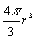 �����߂���B
�����߂���B
�@��ʂɁA���̐}�`��Ⴆ�܂Ȕ̏�ɏ悹�ĕ�Ő�������̖ʐς�S(x)�Ƃ��āA�����[����[�܂ŏW�߂����̂����̂̑̐�V�ɂȂ�B
�@�@�@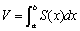
�Ƃ������Ƃ��B���������đ卪�̑̐ς����߂邽�߂ɂ́A�ǂ����̑卪����Ă������A���Ȃ킿���̒����@���ŏ��ɍl��������B�����̎��ƂẮA�܂��݂�Ȃɑ卪�̐�����l���Ă�����āA���̐���ł͂ǂ��̐ς����߂��邩try���邱�Ƃɂ��悤�B
�@�N���A�I���W�i���̐�����Ă��Ă���Ȃ������B
���悵�����͂��A�l�Ȃ��ʂ̐���̒��a�ɐ����ɕ�𗧂ĂăX���C�X���Ă����܂��B
����@�����ł͂܂��A�悵���̕��@�ŗ������Ă݂悤���B�Ƃ���ł��̂Ƃ��̐���͂ǂ�Ȍ`�ɂȂ邾�낤���B
���悵�������Ƃ��Ɖ~����45߂̊p�x�Ő����}�`�ł����璼�p�ӎO�p�`�ɂȂ�܂��B
����@��������͕�����Ղ��ˁB���������đ傫���̈Ⴄ���p�ӎO�p�`��[����[�܂ŏW�߂�����Ƃ������Ƃ��ˁB�ł͂��̒��p�ӎO�p�`�̖ʐς����ɋ��߂悤�B�܂Ȕ̈ʒu��}��x���Ƃ��āA���S�����_�Ƃ���B���_����E��x���ꂽ�_�̒��p�ӎO�p�`�̖ʐς����߂Ă݂悤�B
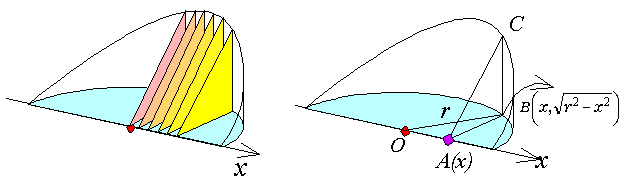
���悵�����͂��B��}�ɂ����āA�O�p�`OAB�͒��p�O�p�`�ŁAOB=r(�~�̔��a)�ł�����A
�@�@�@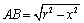
AB=BC��蒼�p�ӎO�p�`ABC�̖ʐ�S(x)�́A
�@�@�@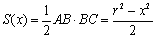
����@���������ł��ˁB���Ƃ͏W�߂ďI��肾�B�Ȃ��W�߂�͈͂́A���_�̉E�����������ŏ\�����B�}�`�̑Ώ̐�����Q�{��������ˁB
���悵����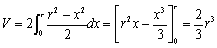 �ƂȂ�܂��B
�ƂȂ�܂��B
����@���������A���̂悵���̒����@������{���B���͒N�����킷��B
�������q���͂��A���ł��B���͂��甍���ɂ�����ǂ����Ǝv���܂��B
���܂Ȃԁ��J�c�����L���ĂȂ��A�����q�B
�������q������[�˂��A�O�������𔖂������Ă������Ƃ�B
���܂Ȃԁ��������A�Z�̐E�l�A�����q���ȁB
�������q�����Ⴉ���Ȃ��ł�B
 ����@�����ł��m���ɖʔ���������ˁB
����@�����ł��m���ɖʔ���������ˁB
�@�ł́A��������Đ��Ĉ�甍�������̂��L����Ƃǂ�Ȑ}�`�ɂȂ邾�낤���B
���悵�����}�̂悤�Ȍ`�ł���ˁB�Ȃ낤�H�A�~�ʂɂ��A�������ɂ��݂���ȁB
�������q���T�C���̃J�[�u�ł���ˁB�m���̌^���������Ă���Ƃ�����Ȍ`������������A���ꂳ��ɕ�������m�����������Ă���B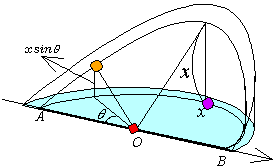 ����@�������̒ʂ�B�����q�̂��ꂳ��͔������ˁB�m���̎����͂��̌`�����̂ˁB�m�F���Ă݂悤���B �}�̌��_O���ނ��̏o���_�ɂ��悤�BO����x���ꂽ�_�Ŕ����Ƃ��A��������̒����A���Ȃ킿�ʂ̒����́A���ax�̉~�̉~���̔����������x���ˁB���̂Ƃ��}�̒[�_A���璆�S�p�ƕ��������ꂽ�_�̔�̍��������߂Ă݂悤�B���S�p�ƂɑΉ�����ʂ̒����́Ax�ƁB���̂Ƃ��E�}�̒�ʂ͔��ax�̔��~���~�����y���W x sin�� �������ɓ������B�ȏ���A����������L����Ɛ}�̂悤�Ȍ`�ɂȂ�B
����@�������̒ʂ�B�����q�̂��ꂳ��͔������ˁB�m���̎����͂��̌`�����̂ˁB�m�F���Ă݂悤���B �}�̌��_O���ނ��̏o���_�ɂ��悤�BO����x���ꂽ�_�Ŕ����Ƃ��A��������̒����A���Ȃ킿�ʂ̒����́A���ax�̉~�̉~���̔����������x���ˁB���̂Ƃ��}�̒[�_A���璆�S�p�ƕ��������ꂽ�_�̔�̍��������߂Ă݂悤�B���S�p�ƂɑΉ�����ʂ̒����́Ax�ƁB���̂Ƃ��E�}�̒�ʂ͔��ax�̔��~���~�����y���W x sin�� �������ɓ������B�ȏ���A����������L����Ɛ}�̂悤�Ȍ`�ɂȂ�B
�@�����ŁA
�@�@�@(u�Cv)=(x�ƁCx sin��)
�Ƃ���ƁA�W�� 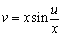 ��������B
��������B
�@�����A����Ŕ������}�`�������Ȑ��ł��邱�Ƃ����������ˁB
�@�ł͎��ɂ��̋Ȑ��̖ʐς����߂Ă݂悤�B
���܂Ȃԁ��Ȃ�����ł��ˁB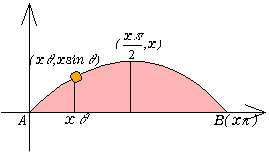 ����@�����}���悭�݂Ă����B���̐����Ȑ��̎����͂Qx�A�ő�l��x���ˁBsin�Ƃ̖ʐςƂ̊W�͂ǂ��Ȃ��Ă��邾�낤�B
����@�����}���悭�݂Ă����B���̐����Ȑ��̎����͂Qx�A�ő�l��x���ˁBsin�Ƃ̖ʐςƂ̊W�͂ǂ��Ȃ��Ă��邾�낤�B
���悵�����������B�c����x�{�Ȃ���x2�{�B������ʐ�S(x)�́A
�@�@�@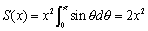
�ł��ˁB
�������q�����������āA�ؓ��~���̑̐ς�
�@�@�@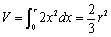
�@�悵���̌��ʂƈ�v�����B
����@���������A�Ō�͂܂ȂԂ̔Ԃ��B
���܂Ȃԁ��^�œo��B�����̓S�l�܂ȂԂ̘r�̍Ⴆ������I���܂��傤�B�����������N�̐���͍H�v�݂͂Ƃ߂邪���܂������B�悵���̐���͎�ۂ��������ǐ����}�`�͂ǂ�����p�ӎO�p�`�B�}�`�ɂ��܂݂��Ȃ��B����ɑ��Ă����q�̂͊m���Ƀ��j�[�N�����ǁA���甍������̂ɂ��������ǂꂾ�����Ԃ�v����̂��낤�B�܊p�̐V�N�ȑf�ނ��ɂ�ł��܂��B���̗��҂̌��_�������̂��c�c
�������q���������͂������瑁�����Ȃ�����B
���܂Ȃԁ��I�z���B���[���A�l�̋Z�͖��Â��āA�~���E�@���Ԃ̕��B
�������q���Ȃɂ���B
���܂Ȃԁ��������畷����B��a�ɏ[�ĂāA�~�̒��S��ʂ�悤�ɁA�g���g���g���g�[���A�������ˏ�ɐ��Ă����B
�������q���Ӂ[��B�܂��ʔ����낻���ł͂����ˁB�ł����̐���ŋ��߂���̂�����B
����@��������͂��낢��ȈӖ��ŋ�����������������Ȃ��B�Ƃɂ����A���߂Ă݂悤���B�܂��A����̐}�`�͂Ȃ낤�B
���܂Ȃԁ��������A���p�O�p�`�ł��B
����@��������ł͂��ɕӂ̒������B���ː���ɐ�킯������A��ʂ̉~�̒��a��x���Ƃ���ƁAx���̐��̕����ƂȂ��p�Ƃ�0����͈̔͂ŕω�����������B�p�x���ƂƂ��āA���p�O�p�`�̂Q�ӂ̒��������߂Ă݂悤�B
���܂Ȃԁ����[���ƁA��ӂ̒����͒�ʂ̉~�̔��ar�ł��B�O�p�`�̍����͒�ʂ̉~�����y���W�̒l�ɓ��������� r sin�Ƃł��B
����@������������Ɛ���̖ʐς�
�@�@�@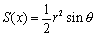
�Ƃ������Ƃ��ˁB
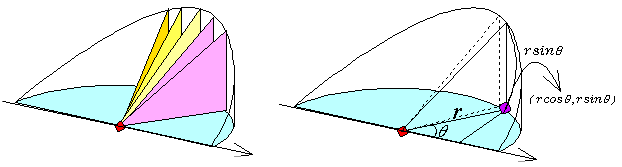
���܂Ȃԁ��͂��A������̐ς́A�Ƃ�0����܂ŏW�߂āA
�@�@�@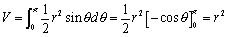
������H�A���������B���ʂ�����Ȃ����B�Ȃ�ŁH
���悵�����v�Z���Ԉ���Ă����Ƃ���͂Ȃ������Ǝv�����ǂȁB�搶�A�ǂ����Ԉ���Ă���̂ł��傤�B
����@�������́A�݂�ȂɎӂ�Ȃ���Ȃ�Ȃ��Ƃ�����B�搶�A���܂܂ʼnR�����Ă����B
�������q�������A���������Ȃ�̂��Ƃł����B
����@�����݂�Ȃɂ͗��̂��X���C�X�����}�`�̖ʐς��W�߂�Ƒ̐ςɂȂ���Ă��������낤�B����͉R�ȂB
���܂Ȃԁ�����̂ǂ����R�Ȃ�ł����B
����@�����l���Ă������B�ʐς��W�߂đ̐ςɂȂ�Ȃ�Ă��Ƃ����肦��Ǝv�������B
���悵��������������Ίm���ɁB�ʐς͓���̂��̂�����A�ǂ�ȂɏW�߂����ē����邱�ƂȂ�ĂȂ��ł���ˁB
����@�������̒ʂ肾�B�ʐς��W�߂�Ƒ̐ςɂȂ�ƌ����������C���p�N�g����������݂�Ȃɂ͂������������Ă������ǁA���m�ɂ����Ɩʐς��W�߂�̂ł͂Ȃ��A�����������̑̐ς��W�߂�Ƃ������ƂȂB
���܂Ȃԁ��卪�̔�����W�߂�Ƃ������Ƃł����B
����@�����������Ė����B�卪���X���C�X�������Đ���������o���킯�ɂ͂����Ȃ����낤�B�ǂ�Ȃɓ����Č�����قǔ������Ă������̌��݂͂���Ƃ����킯���B������ϕ��́A�̐ς��W�߂đ̐ςƂ���������O�̂��Ƃ������Ă������ƂɂȂ�B�ŏ����炱���\�����Ă��܂��ƂȂ��C�Ȃ�����B
�������q���܂��A����������ł��ˁB
����@�������������āA���ܔ����̌��݂���x�Ƃ���ƁA�����S(x)�ł��镔���̑̐ς́AS(x)��x�B�����x�������ɏW�Ă����Ƒ̐ςɂȂ�B�ϕ��̋L�����Sum(�a)��S���㉺�Ɉ����L���č����������ˁB
�@�@�@a����b�܂Ł@Sum(�W�߂�) �@S(x)��x(x������)�@�@�ˁ@�@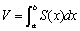 �@(��x��dx�ɑւ��)
�@(��x��dx�ɑւ��)
�Ƃ݂Ȃ������Ƃ������Ƃ��B
�@���Ƃ��悵���̒����@�ł́A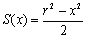 ������ǂ��A����ɔ����̌��݂����������̂ɑ��āA��������ׂďW�߂�ƁA
������ǂ��A����ɔ����̌��݂����������̂ɑ��āA��������ׂďW�߂�ƁA
�@�@�@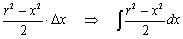
�ƂȂ�B��x���Adx�ɕς�邱�Ƃɒ��ӂ��悤�B
���܂Ȃԁ��ł��ǂ����Ă����q��悵���̐�����Ƌ��߂��āA�l�̂��ƑʖڂȂ̂ł��B
���� ��������ꂽ�}�`���l���Ă����B�����q�Ƃ悵���̐}�`�̌��݂݂͂Ȕ��������Ǔ������݂��낤�B�܂ȂԂ̂͂ǂ����낤�H�B
���܂Ȃԁ������A�l�͕̂��ˏ�ɐ����̂�������݂�����Ă���B
����@�����ł͂���͂ǂ�Ȑ}�`���ȁB
���܂Ȃԁ��͂��A��ʂ̔��~�̒��S�_�Ƃ���p���ɂȂ�܂��B
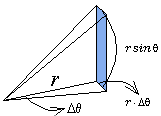 ���悵�����������A�����炱�̏ꍇ�͊p�����W�߂Ă��Ƃ̗��̂ɕ�������ƍl��������B
���悵�����������A�����炱�̏ꍇ�͊p�����W�߂Ă��Ƃ̗��̂ɕ�������ƍl��������B
����@���������������Ƃ��B�p�x�Ƃ���A�����Ȋp�x���Ƒ������Ƃ��̊p���̑̐ς����߂Ă݂悤�B�@�@�Ȃ��A�����p�𒆐S�p�Ƃ���ʂ̒����͐����Ƃ݂Ȃ��Ă����킯������A��ʂ̐}�`�́A�����`�Ƃ��čl���Ă����B
���܂Ȃԁ���������ƁA�ʂ̒����� r���ƁA������ӂ̒����͐�قNj��߂� r sin�Ƃ�����A�����`�̖ʐς́Ar2sin�ƃ��Ƃł��B�p���̍�����r���A���������Ă��̑̐ς́A
�@�@�@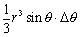
�ƂȂ�܂��B�搶����قǎ������悤�ɁA
�@�@�@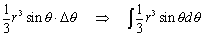
�Ƃ݂�A���߂�̐ς́A
�@�@�@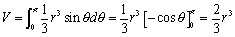
������A�搶�A��v���܂����I�B
�������q���ł����ǐ搶�̎菕����K�v�Ƃ�������A�܂ȂԂ̒����̘r�������������ƂȂ���ˁB
���܂Ȃԁ��Ȃɂ����Ă��B�ڂ��̂��̐�����Ȃ�������搶�͉R�������������Ă��Ƃ���B�l�̉�@��ʂ��Đ^�����\���ꂽ���A�����ɁA�V���������̉\�����J�������Ă��Ƃ���Ȃ����B����点�č����B���ꂱ�������̋Ɉӂ��Ǝv���ȁB
�������q)�ȂɁA��̕�����Ȃ����Ƃ����Ă�̂�B
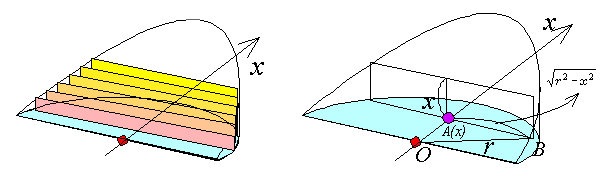
�@���̒����`�̉��̒����́A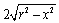 �A�c�̒�����x�ł�����A���̖ʐς́A
�A�c�̒�����x�ł�����A���̖ʐς́A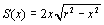 ������0����r�܂ŏW�߂�ƁA
������0����r�܂ŏW�߂�ƁA
�@�@�@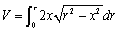
r2-x2=t�Ƃ����āA���ӂ̔������Ƃ�A-2xdx=dt
| x | 0 ���@ r |
| t | r2 ���@ 0 |
 �@���ꂩ��A
�@���ꂩ��A
�@�@�@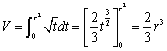
�@���̐���͒u���ϕ��̕��K�̍D��ƂȂ�܂��B
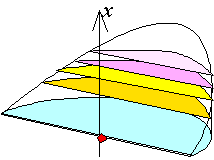
�@���邢�́A��ʂɕ��s�ɃX���C�X���邱�Ƃ��l���鐶�k������ł��傤�B
�@����͉~�ʂɂȂ�܂��B���̉~�ʂ��W�߂Ă݂܂��傤�B
�@��ʂ̔��~�̒��S��ʂ�A���~�ɐ�����x���𗧂āAx���ꂽ�_��A(x)�Ƃ��܂��B
�@���̓_�Ő��Ăł���~�ʂ̖ʐς����߂܂��B
�@�}�`���ォ�猩���낷�ƁA�}�̌`�ɂȂ�܂��B��`ABC����O�p�`ABC������������������̖ʐ�S(x)�ɂȂ�܂��B�~����̓_B���A�����̐��̕����ƂȂ��p���ƂƂ���ƁA
�@�@�@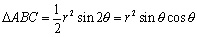
�@�@�@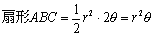
�@����āAS(x)=r2(��-sin��cos��) �ƂȂ�܂��B
�@���āA�����x�ɂ��āA0����r�܂ŏW�߂�����̂ł����Ax�Őϕ����邱�Ƃ͂�����Ƒ�ςł��B�����ŁA�Ƃɑ���p�����[�^�ϕ��Ōv�Z���܂��B
�@�@�@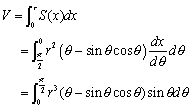
�@�@�@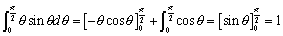
�@�@�@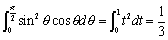
�@�ȏ���A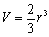 �������܂��B
�������܂��B
�@���������Ă��̐���́A�p�����[�^�ϕ��A�����ϕ��̕��K��ƂȂ�܂��B
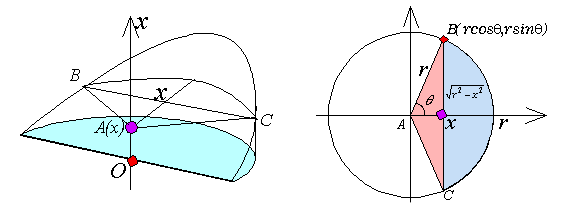
�@���̂悤�ɁA����̐}�`���A���p�ӎO�p�`�A���p�O�p�`�A�~�ʁA�����Ȑ��A�����`�Ƃ��낢��ς��ƁA�����đ̐ς̋��ߕ����H�v����A��ʂ�̊w�K���\�ƂȂ�܂��B���ȏ��̂悤�ɒP���ŏI��炵�Ă��܂��ɂ͂��������Ȃ���ނ��Ǝv���̂ł����B
�@�Ƃ���ŁA��q�ȊO�̐���͉ʂ����Ă���ł��傤���B���Ԃ�A���k�������A�C�f�A�������Ă����Ǝv���܂��B�Ō�ɐؓ��p���̑̐ς́A�d�S�̐����𗘗p����ƁA���̂悤�ɋ��߂邱�Ƃ��ł��܂��B
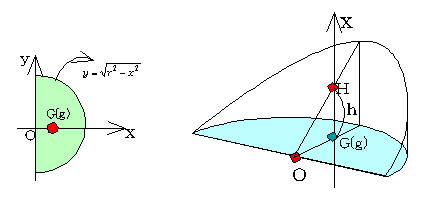
�@�ؓ��p���̒�ʂ̐}�`�̖ʐς�S�Ƃ��A���̐}�`�̏d�SG�ɂ�����p���̍�����h�Ƃ���A�̐�V�́A
�@�@�@S=Sh
�ŗ^�����܂��B
�@���̂̑̐ςʂ��X�L�����������Ƃɋ�Ԃ��X�L��������ƍl����A�����o���܂��B����𗘗p���āA�ؓ��~���̑̐ς��v�Z���Ă݂܂��傤�B
�@�܂��A��ʂł��锼�~�̏d�S�ł����A�E�}x����ɂ���܂��A���̈ʒu��G(g)�Ƃ���ƁA
�@�@�@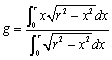
�ŋ��߂��܂�(�ْ����|�[�g�u�l�p�`�̂ւ��v�Q��)�B����āA
�@�@�@(����)=(���ar��1/4�~)= 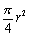 �C�@ (���q)=
�C�@ (���q)= 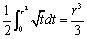 �ł�����A
�ł�����A
�@�@�@�� 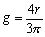
�@�E�}��OGH�͒��p�ӎO�p�`���A
�@�@�@h=GH=OG=g
����āA
�@�@�@