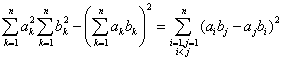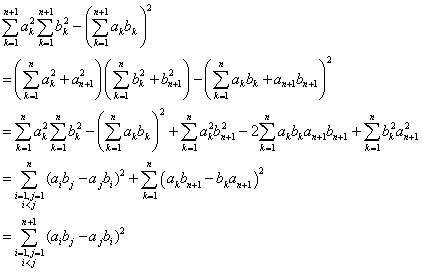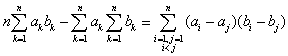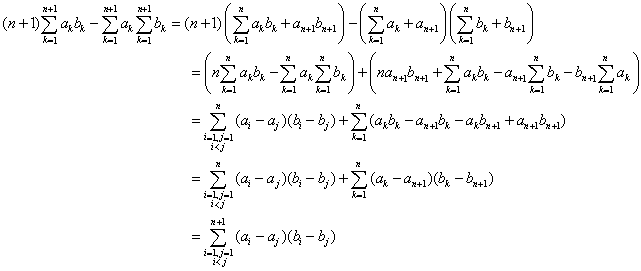|
ex) ���̕s�������ؖ�����B �@(1) (a2+b2)(x2+y2)��(ax+by)2 �@(2) (a2+b2+c2)(x2+y2+z2)��(ax+by+cz)2 |
���悵���� �l��(1)�����܂��B
����@��������B�ł͍Ō�ɓ��������̏������l���悤�B
���܂Ȃԁ��ȒP���B����������������0�̏ꍇ������Aay=bx �̂Ƃ��ł��ˁB
����@��������́A��ŕ\���ƁAa:b=x:y �Ɠ������ˁB�ł́A����(2)���ؖ����Ă݂悤�B
�������q�����̔Ԃ���B
����@�����m���ɂǂ��܂Ƃ߂Ă��������̎������ł͌��������ɂ�����������Ȃ��B������ǂ��������������Ă������Ƃ����̂��s�����̏ؖ��̃L�[�|�C���g�ɂȂ�B��̓I�ɂ݂Ă݂悤�B
�@�܂��A�厖�Ȃ��Ƃ�(2)�̕s������(1)�̊g���ł���Ƃ������Ƃ��B�Ƃ������Ƃ́A(1)�̏ؖ��@�͓��R�g������(2)�̏ؖ��ɂ��ۑ�����Ă���ƍl�����Ȃ����낤���B�����ł��B(1)�̓W�J�̌��ʂ�(2)�̓W�J�̌��ʂ��r���Ă݂Ă����B�Ȃɂ��C�������Ƃ��Ȃ����낤���B
���܂Ȃԁ������[���ƁA(2)�̓W�J�������̒���(1)�̓W�J���������܂܂�Ă���Ƃ������Ƃł����B
����@�������̒ʂ�B�Ƃ������Ƃ́A���̕����͕�����������āA
�@�@�@a2y2+b2x2-2abxy=(ay-bx)2
�ƂȂ�킯���B�ł́A����ȊO�̍��͂ǂ����낤���B
���悵���������悤�ɕ��������ł���Ƃ������Ƃł͂Ȃ��ł��傤���B��������Ɓc�c�c�A
���܂Ȃԁ���������!!�B�������̕��������������́Aa��b�����x��y�ɂ��Ăł���ˁB����A���x��b��c�Ay��z�ɂ��čl��������̂ł͂Ȃ��ł����B
����@�����ǂ����낤���B������Ɗm�F���Ă݂悤�B
�@(ay-bx)2��b��c�����y��z�̊W�ɕς����(bz-cy)2�ƂȂ�ˁB�ł͂��̎���W�J���������A��قǂ�(*)�Ɋ܂܂�Ă��邩�ǂ������ׂĂ����B
�������q��(bz-cy)2=b2z2-2bcyz+c2y2�ł�����c�搶�A�S���܂܂�Ă܂��B
���܂Ȃԁ���������Ƃ��Ƃ́Aa��c�Ax��z�̊W���l����������Ă��Ƃł��ˁB
�@�@�@(cx-az)2=c2x2-2cazx+a2z2
�@���A����́A(*)�̎c��̍��Ɉ�v���Ă���B
����@�����܂Ƃ߂悤�B���������āA
�@�@�@(����)-(�E��)=(ay-bx)2+(bz-cy)2+(cx-az)2��0
�ƂȂ��ďؖ����ł����B�ł́A�Ō�ɓ��������̏������l���Ă݂悤�B
�������q�� �͂��Bay=bx,bz=cy,cx=az�ł��ˁB
����@������̌`�ɂ��Č��₷�����Ă����B
���悵����a:b=x:y,b:c=y:z,c:a=z:x�ł�����Aa:b:c=x:y:z�ƂȂ�܂��ˁB
����@�������̕��������ƌ��₷�����Ƃ�������ˁB�ł́A���܂̍l�������g���āA���̖��������Ă݂悤�B
|
ex) ���̕s�������ؖ�����B �@(1)a��b,x��y�Ƃ���Ƃ��A(a+b)(x+y)��2(ax+by) �@(2)a��b��c,x��y��z�Ƃ���Ƃ��A(a+b+c)(x+y+z)��3(ax+by+cz) |
�������q��(1)�́A ��������Ă݂܂��B���̏ꍇ�A�ꎟ��������A��ʂɂ͈���������������ōl�����ł�����ˁB
���܂Ȃԁ����Ⴀ�A(2)���B
����@�����ł́A�Ō�ɁA���������̃P�[�X���l���Ă݂悤�B�����������ꂽ3�̎������ׂ�0�ɂȂ��������A
�@�@�@(a=b�܂���x=y)����(b=c�܂���y=z)����(c=a�܂���z=x)
�ƂȂ邯�ǁA����͐������ĊȒP�ɂ���Ƃǂ��Ȃ邾�낤�B
���܂Ȃԁ�(1)�̓��������̃P�[�X���P���Ɋg���ł���ƍl����ƁAa=b=c�܂���x=y=z���Ǝv����ł����ǁB
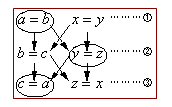 ����@���������ԕs�����̏ؖ��̈������Ɋ���Ă����ˁB�m�F���Ă݂悤�B
����@���������ԕs�����̏ؖ��̈������Ɋ���Ă����ˁB�m�F���Ă݂悤�B
�@�E�}�����Ă����B�@�C�A�C�B�̂��ꂼ��ɂ���Q�̓�������P�̓�����I�ׂ����B���Ƃ��·@�����a=b�A�A�����y=z�A�B�����c=a�B����Ƃ��ꂩ��Aa=b=c��������ˁB���̑I�ѕ����l���Ă����B
�������q���@����x=y�A�A����y=z�A�B����c=a��I�ԂƁAx=y=z�ƂȂ��B
����@�����ǂ������I�ѕ������Ă��A�K��a=b=c��x=y=z�̂ǂ��炩�̎����łĂ���ˁB���ꂩ��܂ȂԂ��\�z�������������̃P�[�X���������������Ƃ��킩�����ˁB
�@���āA�{���̂܂Ƃ߂��B
�@�����̕s�����̏ؖ��́A�����Ƃ��P���Ȑ�Εs�������A�ϐ��𑝂₵�Ċg�����Ă����ꍇ�ɂ́A���Ƃ��Ƃ̕ό`�����ۑ�����Ă��邱�Ƃ𗘗p�������̂��B���ӂ���E�ӂ������āA���������o���o���ɕ������āA�P������g�ݍ��킹���킯�����ǁA�Ⴆ��Ȃ�A�g�����v�Q�[���Ő_�o���������悤�Ȃ��́B�g���킹��y�A����������ΊȒP�ɏE���o���Ă܂Ƃ߂Ă�����Ƃ������Ƃ��B
���܂Ȃԁ��Ȃ�قǁB���������悤�ȋC������B�l�����R�l���܂Ƃ܂�Ȃ��̂̓y�A�����Ȃ�����Ȃ�ł��ˁB
�������q������������肶��Ȃ��ł���B
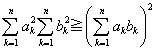 �@�@�@���������́Aak=tbk (k=1,2,���,n)
�@�@�@���������́Aak=tbk (k=1,2,���,n)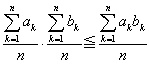 �@�@���������́Aak=aj�܂���bk=bj
�@�@���������́Aak=aj�܂���bk=bj�@�{���̒��ł̏ؖ��@���A�ؖ����ׂ�����W�J(����)���A�g���O�̎��ə��邱�Ƃőg���킹�����߂�̂ɑ��āA��q�̕��@�́A�ϐ���ςݏグ�ďؖ����ׂ��`���\�z���Ă������@�Ƃ�����ł��傤�B�����A�ؖ��̈�ۂŌ����A���̉�@�͍I�߂���悤�Ɏv���܂��B���ʂƕ��@�ǂ���P���Ċg�����邩�Ƃ����I���ł���A��҂̕����g�݂��Ղ��̂ł͂Ȃ��ł��傤���B�������B
|
ex) ���̕s�������ؖ�����B �@(1)|a|��1,|b|��1�̂Ƃ��Aab+1��a+b �@(2)|a|��1,|b|��1,|c|��1�̂Ƃ��Aabc+2��a+b+c |
(1)�̏ؖ�
(2)�̕ʏؖ�
�@(1)���玩�R�Ǝ��ό`��������A(*)���K�R�I�ɗv������邱�Ƃ�������ł��傤�B
�@���̏ؖ��@���O�p�s�����ɓK�p���Ă݂܂��傤�B
|
ex) ���̕s�������ؖ�����B �@(1)|a+b|��|a|+|b| �@(2)|a+b+c|��|a|+|b|+|c| |
(1)�̏ؖ�
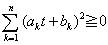 ���瓱����܂��B
���瓱����܂��B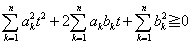 ����A���̂Q���������̔��ʎ����c�Ƃ���ƁA
����A���̂Q���������̔��ʎ����c�Ƃ���ƁA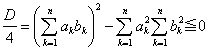 ��蓾���܂��B
��蓾���܂��B