

<先 生>なに!、何かトラブルがあったのか!。
<かず子>やだ〜、違うわよ、先生。2人でマジメに勉強してたのよ。で、そのときにまなぶが三角関数の合成って、何かしっくりこないっていいだしたんです。
<先 生>へぇーっ、二人で勉強ね。で、トラブったのかい。
<かず子>違うってば。結論をいうと合成って必要なのかなってことなんです。あっ、まなぶとよしおが来た。まなぶ、さっきの話してよ。
<まなぶ>うん。この間の授業で合成って妙な公式を教えてもらいましたよね。アレッて何ですか。
<先 生>ぶっきらぼうだな質問だな。
a sinθ+b cosθ
と表される式をどうしたら sin(θ+α)に変形できるかってことだ。
<まなぶ>やだなあ、先生。同じようにぶっきらぼうに応対するなんて案外大人気無いですね。じゃあもう少し詳しくいいます。教科書には合成の公式はこんなふうに書いてますよね。
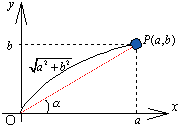
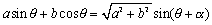 ただし、 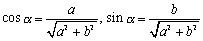
|
この式の定数a,bと sinθ,cosθは、どんな関係になっているのかよく分からないんです。適切な言葉がみつからないけれど、なんか定数a,bは角θの三角関数にくっついている贅肉としか思えないんですけど。
<かず子>実は、私もまなぶと同じ印象をもっていたんです。どうして(a,b)なんて点が唐突にでてくるのか不思議で、公式として単純に割り切ることがしっくりと納得できない。私は(a,b)は三角関数の寄生虫のように感じていたんです。
<先 生>みんなずいぶん手厳しいきつい言い方するね。よしおも同意見かな。
<よしお>僕はこの公式を変形のマニュアルとみて「こうすれば上手く合成できる」って程度で押さえていました。この公式を使えばいろいろな問題が簡単に求められるわけだから、その道具としての価値を考えればいいんです。でも先ほど、まなぶとかず子の合成って必要ないのではという考えの理由を聞いてみたら、それも一理あると思ったんです。
<先 生>どういうこと。
<かず子>私達、次の問題を解いていたんです。
ex) 方程式 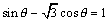 を解け。ただし、0°≦θ≦360°とする。 を解け。ただし、0°≦θ≦360°とする。
|
問題集の解答は、次のようになっています。
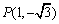 をとると、
をとると、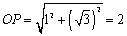
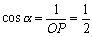
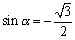 であるから、α=-60°としてよい。
であるから、α=-60°としてよい。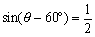
<先 生>一般的な解法だね。
 <かず子>そうしたらまなぶがですね。この問題もっと簡単にできるんじゃないかって言い出したんです。
<かず子>そうしたらまなぶがですね。この問題もっと簡単にできるんじゃないかって言い出したんです。
<まなぶ>そのあとは僕が説明するよ。先生は授業中、いつも三角方程式や不等式を解くときに、
「コサインはx、サインはy」
を意識しろっていってたじゃないですか。だからこの場合も、与式を
cosθ=x,sinθ=y
っておいてみたんです。すると
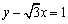
となりますよね。
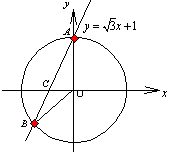
あとはこの直線と単位円x2+y2=1との交点を求めればいいと思うんです。そうしたら今度はかず子が、交点を求めなくてももっと簡単に角度を調べる方法をみつけたんです。
<かず子>私の番ね。
わざわざ面倒な連立方程式を解かなくても、直線がx軸の正の向きとなす角をαとすると、直線の傾きが tanα に一致することを利用すれば求められます。
直線の傾きは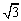 だから、
だから、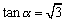 。よって、図より∠ACO=60°となるから、
。よって、図より∠ACO=60°となるから、
∠OAC=30°
∴∠AOB=120°より求める角度は、θ=90°,210°
となりますよね。
<まなぶ>合成って、サインとコサインがごちゃごちゃ混じっている式をサインの三角関数で揃える式だと思うんですけど、いまのように、直線と円の交点である円周上の点の角度と考えればそんな必要はないんじゃないだろうかってかず子と話し合っていたんです。
<よしお>確かにそう考えると、不等式なんかも、不等式の表す領域を考えれば合成なんかを使うよりずっと簡単に求められますよね。例えば、問題集の次の例題をためしにやってみたんです。
| ex) 不等式 sinθ>cosθ (0°≦θ<360°)を解け。 |
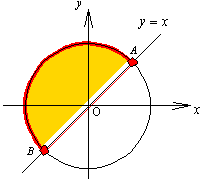 これなんかも、不等式
これなんかも、不等式
y>x
の表す領域にある円周上の点を求めればいいわけですから、右図より
45°<θ<225°
と簡単に求められますよね。
だから確かにかず子とまなぶがいうように、合成の必要性ってあんまりないようにも感じるんです。
<先 生>なるほど。面白い話題かもしれないね。よし、それでは次の問題を解いてごらん。
ex) 不等式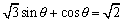 (0°≦θ<360°)を解け。 (0°≦θ<360°)を解け。
|
 <まなぶ>では僕がチャレンジ。
<まなぶ>では僕がチャレンジ。
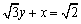
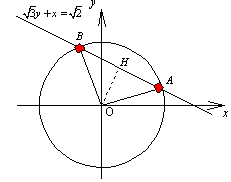
えーっと、この直線がx軸となす角をαとすると、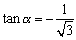 よりα=150°となります。
よりα=150°となります。
だから円周上の点の角度を求めると……、あれ、おかしいな。上手く求められないや。
<かず子>そうね。それじゃ、x2+y2=1 との交点を求めればいいんじゃないの。
xを消去して、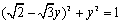 だから、
だから、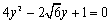
わっ、だめだわ。これでも求められないわ。
<まなぶ>ショック、悔しいなあ。求められない場合もあるんだ。今回はちょっとした発見だと思ってたのに。
<先 生>いや、求められないわけではないと思うよ。
よしお、円の中心である原点と直線との距離dを計算してごらん。
<よしお>あっ、はい。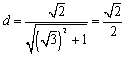 です。なるほど。これを利用するんですね。
です。なるほど。これを利用するんですね。
<まなぶ>よしお、何とかなるのかい。
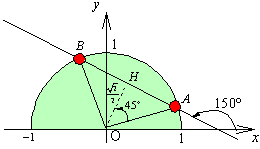 <よしお>ああ。だって原点から直線に下ろした垂線の足をHとすると、△OAHにおいて、
<よしお>ああ。だって原点から直線に下ろした垂線の足をHとすると、△OAHにおいて、
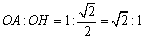
これから△OAHは直角二等辺三角形だから、∠AOH=45°。
ここで、OHは直線に垂直だから∠COH=60°であることを利用すれば、
∠COA=∠COH−∠AOH=15°
先生、出せますね。
<かず子>そうするともう一つの角度は、15°+90°=105°ね。やった、まなぶ、私たちの努力は無駄ではなかったわ。
<まなぶ>だめだよ、かず子。確かに点と直線の距離の公式を使えば解けるみたいだけど、この方法が合成を使った解法と比較して飛び抜けて簡単で手軽な求め方とは思えないもの。残念だけど、やっぱり合成公式の壁は厚かったということだよ。
<かず子>でも、sinθ>cosθみたいな問題だと合成より圧倒的に簡単にできるじゃないの。
<まなぶ>そりゃ、そうだけど……、完全に合成の牙城を崩せたわけではないだろ。残念だなあ。
<先 生>まなぶはずいぶんと合成の公式に敵対心を持っているみたいだね。その理由はa,bとsinθ,cosθの関係が見えないから疎ましいということだったみたいだけど、それじゃ、まなぶの気持ちに応えてこの係数と三角関数の深い関係を探ってみようか。
<まなぶ>えっ、何か秘密があるんですか。
<先 生>結論を急がないで。まず、みんなは合成の変形はもともとは何を利用しているか知っているよね。
<かず子>はい。もちろん加法定理です。授業で先生は、加法定理が展開なら、合成は因数分解を表すようなものだっていってました。
<先 生>そうだね。例えば、
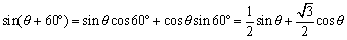
という計算に対して、逆に右辺から左辺を変形したものが合成というわけだ。
ところでみんなは右辺を変形したら必ず左辺になると思うかな。
<まなぶ>何言ってるんですか。変形できると先生が教えてくれたんじゃないですか。ひょっとしたら先生が授業で間違ったことを教えたことが原因で、僕が合成に妙な違和感を抱いているんじゃないのですか。
<先 生>勘ぐりすぎだ。まなぶじゃあるまいし、大事なことは間違えないさ。まあ、確かにみんなにそう教えたんだけど、でも考えてごらん。加法定理って sin(α+β)だけかな。
<まなぶ>先生、はぐらかさないで。そりゃ、cos(α+β)だって、tan(α+β)だっていろいろあるけど、……、あっ、どうしていつも同じ変形なんだ。
<かず子>何か分かったのまなぶ。
<まなぶ>だってね。例えば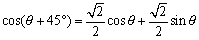 となるだろ。この右辺は合成する前の式そのものだけど、でも左辺はコサインについての合成になっているじゃないか。
となるだろ。この右辺は合成する前の式そのものだけど、でも左辺はコサインについての合成になっているじゃないか。
<先 生>いいぞ、まなぶ。「コサインの合成」、まさにその通り。
<よしお>ということは合成の仕方は一通りではないということですか。
<先 生>確認してみようか。
ex) 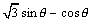 を合成せよ。 を合成せよ。
|
<かず子>これ、前の授業でやったわ。点 を座標平面上にとって……。
を座標平面上にとって……。
<先 生>それじゃ、前と同じ結論がでてしまうだろ。この変形のポイントは、加法定理を利用てぎる形に持ち込むということだ。例えば、 とみることができれば、与式は
cosαsinθ+sinαcosθ=sin(θ+α)
と変形できるだろ。
<かず子>でもその式おかしいわ。それだと三角関数の値が1を超えてしまってる。
<よしお>それもそうだけど、cosαとsinαの平方の和が1であるという性質に反してるよ。
<先 生>先生は、例えばっていったぞ。確かにこのままでは無理だ。実際、平方の和を求めると4になってしまうね。そこでこれが1になるように係数調整をする必要がでてくる。なんで割っておけばいいだろう。
<まなぶ>4で割るんですよね。
<先 生>よく考えてごらん。「ある数で割ったものを平方して和をとったら4になる」ってことだよ。
<まなぶ>あっそうか。平方する前に割るんだからもともとは全体を2で割っておけばいいということですね。
<先 生>その通り、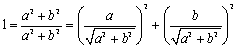 とみればいい。変形してみよう。
とみればいい。変形してみよう。
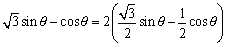
ここで、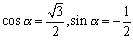 とおけば、たしかに cos2α+sin2α=1となるね。
とおけば、たしかに cos2α+sin2α=1となるね。
以上より、(与式)=2sin(θ+α) と変形できることになる。ところでこの場合のαは簡単に求まるね。
<かず子>えーっと、第4象限の角だから、α=-30°ですね。
<先 生>結局、座標平面上に点をとらなくてもできてしまったね。うん?、まなぶ、なんか不満そうだね。
<まなぶ>確かに、合成は加法定理計算の逆演算ということはよく分かったけど、先生が言ってたほど深い関係には思えないよ。それに、角度αを求めるのも何か面倒だし。だいたい、(a,b)というように点をとることは、角度を視覚的にみてラクをするためですよね。先生の方法だと何か逆行しているような気がするんですけど。
<先 生>ずいぶん手厳しい意見だね。先生は最初、「例えば○○とみる」っていっただろ。では、今度はまなぶ自身が指摘していた「コサインの合成」ってことを考えてごらん。
<まなぶ>コサインの合成ですか?ということはコサインの加法定理の逆だから……あっ、そうか。なにも、コサイン、サインの順番に係数を読み替える必要はないんだ。加法定理のどれかの形にまとめれば変形はできるわけですよね。だから例えば、
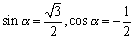
とおいてやると、コサインの加法定理が使える。すなわち
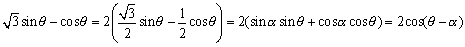
ここで角度αは、ええっと、α=120°ですね。これでもいいんだ。ちょっと角度を求めるのが大変だけど……。
<かず子>まなぶ、なにもマイナスを含めて置き換える必要はないんじゃないかしら。例えば、
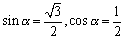
とおくのよ。そうすると、簡単にα=60°が求められて、

となるわ。
<よしお>それならば、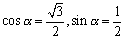 としたらどうだろうか。角度は、α=30°で、サインの差の加法定理から
としたらどうだろうか。角度は、α=30°で、サインの差の加法定理から
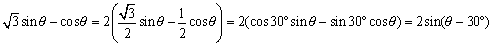
となるだろ。
<先 生>素晴らしい。三者三様の変形ができたね。どうだろう、分かっただろうか。みんなが求めた式変形それぞれが正しい答えなんだ。すなわち、合成が加法定理計算の逆算なら、その式変形はけっして固定化されるべきではな、加法定理の公式の数だけ変形も生まれてくる。そこらへんのところが妙に教科書なんかはマニュアル化されて「なにがなんでもサイン」になってしまっているんだ。
<まなぶ>なるほどね。先生のいってることは分かったけど、でも、それは単にa,bの見方を変えただけで、角度θとの深い関係はやっぱり見えないと思うんですけど。
<先 生>実は、まなぶ自身が言った「コサインの合成」って言葉がその秘密を握っているんだ。
<まなぶ>えっ、そうなんですか。でもどうして??。
<先 生>合成が加法定理の逆算なら、その加法定理は何から導かれたものであったろうか。
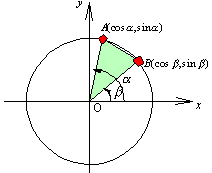 <よしお>第3余弦定理だったと思います。単位円周上の2点をA(cosα,sinα),B(cosβ,sinβ)とすると、△AOBにおいて、∠AOB=α−βだから、
<よしお>第3余弦定理だったと思います。単位円周上の2点をA(cosα,sinα),B(cosβ,sinβ)とすると、△AOBにおいて、∠AOB=α−βだから、
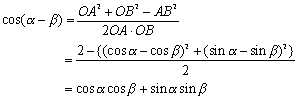
ということですよね。
<まなぶ>すごい。さすが、よしおだな。
<先 生>すなわち、コサインの加法定理は、円周上の2点A,Bに対して、∠AOBの余弦を求める公式だったということだね。それではだ。それを合成に当てはめてみよう。ただし、まなぶのいった「コサインの合成」で考えるために、もともとの式を a cosθ+b sinθとしておこう。まず、円周上にA(a,b)なる点をとってごらん。
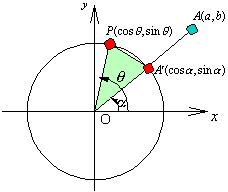 <まなぶ>なんか、また教科書の考え方に戻ってしまったような……。
<まなぶ>なんか、また教科書の考え方に戻ってしまったような……。
<先 生>いいから黙って点をとる。次にOAの線分上あるいは点Aの延長上にある単位円周上の点を求めてみよう。
<かず子>大きさを1にすればいいんだから、点Aの座標を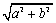 で割ればいいですね。
で割ればいいですね。
<先 生>その点をA'とおき、x軸の正の方向OA'とのなす角をαとすると、A'(cosα,sinα)となるね。
ここで、P(cosθ,sinθ)とすれば、さて a sinθ+b sinθはどんな意味になるだろう。
<かず子>∠A'OPのなす角の余弦ですか。
<まなぶ>かず子、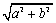 で割ったことを忘れているよ。だから、
で割ったことを忘れているよ。だから、
(∠A'OPのなす角の余弦)×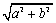
ですよね。
<先 生>その通り。では、もっと遡ってみようか。余弦はもともとどういう定義だったろう。
<かず子>直角三角形で考えられる6つある2辺の比のひとつです。
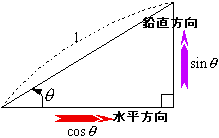 <先 生>それを視覚的に表すと……。
<先 生>それを視覚的に表すと……。
<まなぶ>ああ、分かった。三角比におけるピタゴラスの定理のことですね。
図を書くと、右のようになります。
<先 生>傾斜θの長さ1の斜辺を登るとき、水平方向、垂直方向の移動距離がそれぞれ、余弦、正弦の値だったよな。そこまで確認できればもう説明の必要はないと思う。
<まなぶ>えっ!、よく分からないのですが。結論が出たってことですか、あのう合成の秘密って……。
<先 生>みんなはもう合成公式を使えるようになっているよ。いままでの問題をもう一度解いて見ようか。
|
ex)次の方程式・不等式を解け。 (0°≦θ<360°) (1) 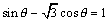 (2) 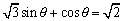 (3) 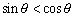 (4) 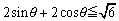
|
<先 生>まず(1)だ。コサインの合成を考えるために、
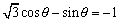
とみよう。(a,b)に相当するものが円周上の点になるように、与式の両辺を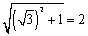 で割っておく。
で割っておく。
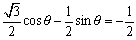
そこで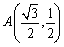 とすると、x軸とOAとのなす角は何度だろう。
とすると、x軸とOAとのなす角は何度だろう。
<まなぶ>第1象限で考えればいいから簡単。α=30°です。
<先 生>ここで右辺の値−1/2がコサインの値であるからその角度を求めてみよう。
 <かず子>はい第2象限の角で考えてα=120°です。
<かず子>はい第2象限の角で考えてα=120°です。
<先 生>θとOAがそれぞれX軸となす角を表しているから、このコサインの値はθ−30°のことだ。したがって、θ−30°=120°より、θ=150°となる。
<まなぶ>あれれ!。いつのまにか答えがでてる。でも先生、もうひとつ答えがありましたよね。
<先 生>さきほどかず子は−1/2となる第2象限のコサインの値を考えたけど、同じように第4象限でも求められる。
<よしお>でも先ほど先生がおっしゃったコサインは水平方向の値とみれば、この場合は150°である円周上の点から直線OAに垂直な直線を引いて、もう一度円周と交わる点を求めればいいですよね。
<先 生>よしおは、合成の本質が見えてきたみたいだね。その通りだ。したがって30°から負の向きに120°を戻せばいい。すなわち角度は−90°。0°≦θ<360°の範囲に注意して、270°が残りの解となる。
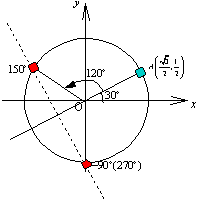
 <かず子>なんか全然計算しないうちに答えがでてしまうんですね。(2)は私にやらせて貰えますか。
<かず子>なんか全然計算しないうちに答えがでてしまうんですね。(2)は私にやらせて貰えますか。
まず両辺を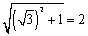 で割って、
で割って、
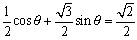
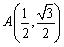 とすると、x軸の正の方向とOAのなす角度は60°。
とすると、x軸の正の方向とOAのなす角度は60°。
後はコサインが右辺の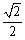 となる角度を求めて、60°±45°より、15°,105°が答えです。
となる角度を求めて、60°±45°より、15°,105°が答えです。
わーっ、なんでこんなに簡単にでるの。私たちの苦労ってなんだったの。
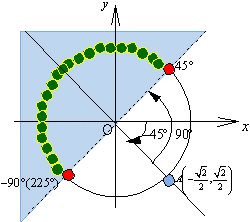 <よしお>じゃ、(3)の不等式の問題は僕に解かせてください。
<よしお>じゃ、(3)の不等式の問題は僕に解かせてください。
まず、cosθ−sinθ<0より、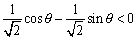
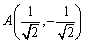 とすると、OAとx軸のなす角は−45°。コサインが0となる値は±90°だから、
とすると、OAとx軸のなす角は−45°。コサインが0となる値は±90°だから、
−45°±90°=−135°,45°
さてと、ここから不等式の範囲を考えるわけですね。円周上45°の角度の点から直線OAに垂直な直線を引くと、コサインが0より小さい値はその直線の左(上)の部分になりますから、その範囲にある円周上の点が求める範囲です。
したがって、45°<θ<225°となります。
この問題だけでいえば僕がさっきやったy>xとみる解法の方がラクにできるけど、これも分かりやすい方法ですね。
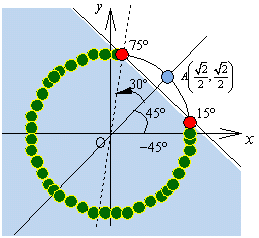 <先 生>では最後の問題をまなぶに締めてもらおう。
<先 生>では最後の問題をまなぶに締めてもらおう。
<まなぶ>うーん。とりあえず解きます。
両辺を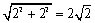 で割って、
で割って、
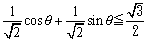
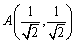 とすると、OAがx軸となす角は45°。
とすると、OAがx軸となす角は45°。
コサインが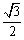 となる値の1つは30°だから、あとは右図より、0°≦θ≦15°,75°≦θ<360°
となる値の1つは30°だから、あとは右図より、0°≦θ≦15°,75°≦θ<360°
先生、解けました。
<先 生>まなぶ、まだなんか不満が燻っているようだけど。
<まなぶ>合成のヒミツってやつが、なんかしっくりと呑みこめないんです。
先生は、a cosθ+b sinθのa,bと角度θには深い関係があるといったでしょ。結局それってどんな関係だったんでしょうか。
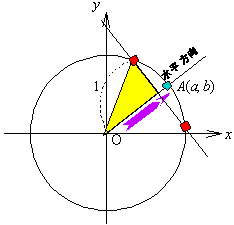 <かず子>わたしもそれが気になっていたんです。
<かず子>わたしもそれが気になっていたんです。
<先 生>それはさっきまなぶ自身が答えていたじゃないか。コサインは斜辺が1の直角三角形の水平方向の値だったな。ではその直角三角形を線分OAに乗っけてみてごらん。
右図のようになったかな。さあ、a,bってどんな働きをしている。
<まなぶ>コサインの水平方向の値でこの場合はそれが直線OAに乗っているということだから、……あっ、そうか。シセン、始線でしょう、先生。
<先 生>やっとヒミツを探り当てたね。コサインやサインのa,bの値は実は角度を測り始める出発点を示していたんだ。
だからまなぶやかず子がいっていたように「贅肉」とか「寄生虫」ように邪魔者扱いするなんてとんでもないことだ。a,bは角度の元を示す基軸でありこれなしでは考えられない。一見すると疎ましい存在がじっくり観察すると実は大事な存在であったということはよくあることだろ。
なあ、まなぶとかず子、そう思わないかな。
<かず子>やだわ、先生ったら。
<まなぶ>かず子、先生は何をいってるの?。
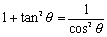 は、もとをただせば、sin2θ+cos2θ=1をcos2θで割ったものではあるが、コサインの実力を認めながらも日の目をみることはないのである。
は、もとをただせば、sin2θ+cos2θ=1をcos2θで割ったものではあるが、コサインの実力を認めながらも日の目をみることはないのである。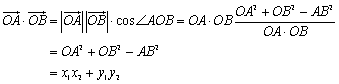
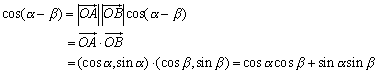
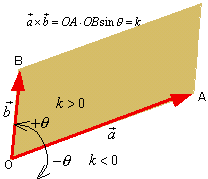 平面上においては、ベクトル
平面上においては、ベクトル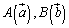 に対してその外積は、
に対してその外積は、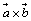 =±(OA,OBを2辺とする平行四辺形の面積)
=±(OA,OBを2辺とする平行四辺形の面積)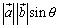
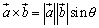
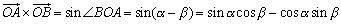
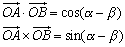
 右図において
右図において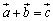 より、
より、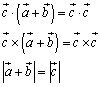
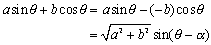
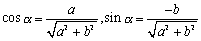 である。
である。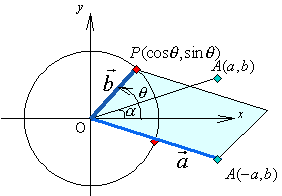 最後に、まなぶとかず子の関係についてちょっと。
最後に、まなぶとかず子の関係についてちょっと。