金太郎アメの切り口

＜先　生＞今日は，群数列の問題を考えてみましょう。群数列とは，与えられた数列に，規則性をもって項の間に仕切をいれていき，グループ分けしてできる数列のことです。次の問題を見てください。

　ベースになった数列（原数列）{a_n}は，初項1で交差3の等比数列だけど，さてこの数列に仕切をどうやっていれていったのだろう。

＜かずこ＞仕切で区切られた項数をみると，

　　　1，3，5，7，……

となっていますから仕切で区切られたグループの項数が，左から順に，初項1で公差3の等差数列になっていると思います。

＜先　生＞そうだね。このとき，仕切で分けられた項のグループを左から順に，

　　　第1群，第2群，第3群，………第n群

と呼ぶことにします。では，ちょっとグループに分けた各群の数列の性質を調べてみよう。代表して，第n群について考えれば十分だね。

　まずは，原数列が等差数列だったんだから，どこで区切っても群数列が公差3の等差数列なるのは当たり前だよな。さあ，あと，分かってることないかな。

＜まなぶ＞項数が分かるかと思います。第n群の項数は，等差数列の第n項を考えると，2n−1個になります。

＜先　生＞うん，だいぶ見えてきたね。第n群の数列は，公差3の等差数列で，項数が2n−1個ということが分かった。では，あと数列を決定するには何が必要だろうか。

＜よしお＞初項かな……？

＜先　生＞もっと自信をもって発言しよう。その通りだ。実は，これが問1の設問になっている。各群の第1項の値がわかれば，数列を決定するすべての要素が分かるということです。では，この第1項はどうやれば求められるだろう。

＜生徒達＞………

＜先　生＞何を難しく考えているのかな。各群の第1項目の数の規則性を調べればいいんだから，やるべきことはきまっているだろ。

＜よしお＞あっ，そうか。抜き出せばいいんだ。

＜先　生＞そうだね。各群の第1項を抜き出したものを数列と考えて，規則性を見つければいいんだ。

　さあ，それでは，各自抜き出して調べてごらん。

＜まなぶ＞　1，4，13，28，49，………　等差でも等比でもないし，うーん。分からない。

＜先　生＞諦めちゃいけない。一般に，規則性がよく分からない数列の場合は，どうするんだっけ。

＜かずこ＞階差だわ！階差をとればいいんですよね。隣接2項の差をとっていくと，

　　　3，9，15，21，………　　　　　　　　……(＊)

　分かりました。階差数列が，公差6の等差数列になってます。

＜先　生＞では，よしお，この階差数列{b_n}の一般項を求めるとどうなる。

＜よしお＞初項3で公差6だから，

　　　b_n =6n-3

となります。

＜先　生＞うん，だいぶターゲットに近づいてきたね。それでは詰めだ。第n群の第1項目は，(＊)の第n項目なんだから，階差数列{b_n }を利用して計算してみよう。

＜まなぶ＞先生，できました。

n=1の場合も含められるから，第n群の1項目の値は，3n²-6n+4になります。

＜先　生＞これがex）の(1)の答えだ。あとは，簡単だよね。(2)をかず子，解いてごらん。

＜かず子＞第n群は，第1項が3n²-6n+4で，公差3，項数が2n−1の等差数列だから，その和Sは，

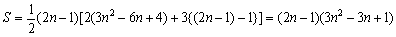
です。

＜先　生＞では，最後(3)だ。1000を第n群の中の項とすると，次のような関係式が作られる。

　　　3n²-6n+4≦1000＜3(n+2)²-6(n+1)+4

整理して，n(n-2)≦332＜(n-1)(n+1)

これを満たす自然数nはなんだろう。かず子，求めてごらん。

＜かず子＞えーと，332=3.32×100 で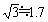，ですから，n=17，18，19ぐらいで考えて，

　　　19×17=323， 20×18=360　

できました。n=19だから，第19群です。

＜先　生＞では，最後に項数をよしおに計算して貰おう。

＜よしお＞ 第19群の第1項は，

　　　3×19²-6×19+4=973

ですから，項数mは，

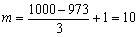
従って，数1000は，第19群の第1項から数えて10番目の数です。

＜先　生＞さあ，本時の復習だ。原数列を適当に区切って郡数列を作っても，もとの数列の性質は変わるわけじゃないんだ。金太郎アメをみんなは知っているだろう。どこできっても金太郎の顔ででてくる。ただ，ちょっとずつ顔は違ってくるわけだから，切ったときのその切り口の顔がどうなっているか，見つめてやればいいってことなんだよ。

Ｎｏｔｅ）

　群数列の定義についてですが，本文の説明は適当ではありません。原数列を仕切って作られる場合と，逆に共通性質をもった数列を仕切りごとに並べた数列も考えられるでしょう。

　次に，本文の解答についてですが，後半の(3)については，数1000は原数列において，

　　　1000=3n-2より，n=334

ですから，この項数から求める方が自然だと思います。

　第n群の第1項a_Nまでの項数は，

　　　a_n=3n-2=3n²-6n+4

　　　n=n²-2n+2

これから，

　　　n²-2n+2≦334＜(n+1)²-2(n+1)+2

を満たすnを求めます。本文では，第n群の第1項目が何かということを通常の解答のように，項数を調べて求める方法をとらなかったので，敢えて，項の値から求めてみました。

　ところで，本文では，第1項を抜き出して作られる数列の階差数列から，第n群の第1項を求めていますが，この解答には，ひとつの不安があります。それは，階差数列を等差と予想することに対してです。(＊)がその階差数列にあたりますが，果してこの数列は本当に，等差数列なのでしょうか。各群の第1項を高々4，5個抜き出して断定することは，危険過ぎるのではないでし ょうか。

　そこで，このことについて，少し考えてみましょう。

　いま，初項a，公差dの等差数列{a_n}を原数列とし，次のように，群数列の仕切を，初項p，公差qの等差数列になるように入れていきます。

a₁，a₂，…，q_p，｜a_p+1，a_p+2，…，a_2p+q，｜a_2p+q+1，a_2p+q+2，…，a_3p+3q，｜a_3p+3q+1，… ………(♯)

　このとき，各群の第1項目の値を抜き出して作った数列の階差をとっていくと，原数列の公差がdであることより，下図のように，階差数列{b_n}は，初項pdで公差qdの等差数列となります。

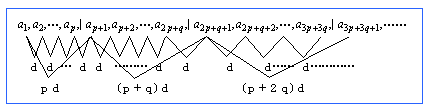
　よって，階差数列の一般項が，b_n=pd+(n-1)qdとなることから，第n群の第1項a_nは，各群の項数から作られる数列の初項から第(n−1)項までの和をSとすると，

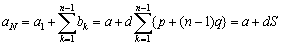
で得られます。また，原数列の初項から第n群の第1項までの項数Ｎは，

　　　a_n=a+(n-1)d=a+dS　より　　n=S+1

となり，通常の群数列の解法で導き出される結果と一致するわけです。

　同様に，原数列に初項p，公比qの等比数列になるように仕切を入れ，群数列をつくると，各群の第1項を抜き出して作られる数列の階差は，

　　　pd，pqd，pq²d，pq³d，……

から，初項pd，公比qの等比数列となり，まったく同様の結果が得られます。

　このように，原数列が等差数列ならば，どのような規則性で仕切りをいれても，各群の第1項を抜き出すと，

　　　仕切られた項数×原数列の公差

が階差数列の2項の差として現れることになります。

　例えば，次の群数列は，公差2の等差数列を，各群の項数が1，4，9，16…と平方数になるように，区切っていますが，各群の第1項を抜き出して作られる数列の階差数列は，公差2×平方数より，2，8，18，32，……となるわけです。

1，｜3，5，7，9，｜11，13，15，17，19，21，23，25，27，｜29，31，33，35，37，39，41，43，45，47，49，51，53，55，57，59，｜61，……

　これに対して，原数列が等比数列の場合は，各群の第1項から作られる数列の階差数列{b_n}を利用して求めることは，理論上可能ではありますが，非常に複雑な計算となってしまいます。高々4，5個抜き出しての判断すらできないでしょう。

　例えば，原数列が初項a，公比rの数列で，(♯)のように仕切り群数列をつくるとき， {b_n}の一般項は，

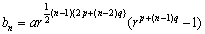
で与えられます。