

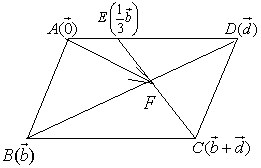
ex) 平行四辺形ABCDにおいて、辺ADを1:2の比に内分する点をEとし、BDとCEの交点をFとする。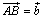 , ,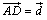 として、次の問いに答えよ。 として、次の問いに答えよ。(1) 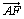 を、 を、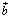 , ,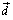 で表せ。 で表せ。(2) 比CF:FEを求めよ。 |
 <まなぶ>ずいぶんおとなしい問題ですね。
<まなぶ>ずいぶんおとなしい問題ですね。
<かず子>まなぶ、棘があるわよ。標準的問題ってことですよ、先生。
<先 生>ではその標準的問題を解いてもらおうか。
<よしお>では、僕が。
各頂点に座標を入れていきます。
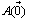 ,
,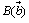 ,
,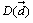 ですから、
ですから、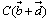 ,
,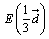 となります。
となります。
次に点Fを2線分の交点とみると、
Fは線分EC上の点より、
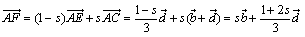 ……(*)
……(*)
また、Fは線分BD上の点より、
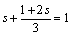
これより、s=2/5だから、
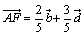
となります。
<かず子>さすが、よしお。完璧ね。では(2)は私がやるわ。
よしおが解答した(*)の式より、
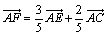
だから、CF:FE=3:2です。
でも先生、本当に聞きたい問題は、これからなんかあるんですよね。
<先 生>なんか最近、かず子の性格、ずいぶんまなぶナイズしてないかな。確かにこれから言うことが大切なことなんだ。よしおはどうして(1)から解いたのかな。
<よしお>通常、小問に分かれた問題は、解答の誘導やヒントが与えられているという点からも(1)、(2)のように問題番号順に解くのではないですか。
<かず子>よしお、先生がいいたいのは、たぶん(2)の答えの方が簡単に求められるってことだと思うわ。
<先 生>かず子、先生ちょっと君のことが心配になってきた。勘ぐりや先読みと、数学的推論は違うからね。そこのところ履き違えてしまうと誰かさんのようになってしまうよ。
 <まなぶ>先生、誰かさんって、誰のことですか。でも先生、僕、分りましたよ。
<まなぶ>先生、誰かさんって、誰のことですか。でも先生、僕、分りましたよ。
<先 生>かず子が代弁していたからずいぶん静かだと思っていたら……、で、どういうことだい。
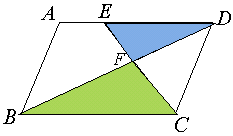
<まなぶ>右図のように色を塗ってみるとすぐ分ります。
△EFDと△FCBは相似ですよね。すると、相似比を考えると、
CF:FE=BC:ED=AD:ED=3:2
ほら、でちゃいました。
<かず子>まなぶ、凄いわね。本当だ。私たち、なんであんな面倒なベクトルの計算してたんだろう。
<よしお>確かに(2)が分かってしまえば、(1)の問題は、
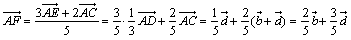
とだせるね。
<先 生>あるいは、BF:FD=3:2も明らかだから、Fを線分BD上の点とみると、すぐ求められる。
ところでかず子は、「なんでベクトルの計算をしてたんだろう」っていっていたね。本当に、何故だろう。
<まなぶ>だって、問題文で位置ベクトルが与えられていたら、当然ベクトルでの解答を要求されていると考えるのは当たり前ではないでしょうか。
<先 生>と、いつもの先読みをまなぶはするわけだ。
<まなぶ>ちょっと嫌味な言い方のような気もするけど、まあそうです。正確にいうと「思い込み」でしょうが。
<先 生>失礼。でもそこのところが大事なんだ。本来、問題を解くときには諸君が蓄えた問題解決法という道具箱から最良の方法である引き出しを選び出してやればいいんだけど、ある単元ばかりやっていると何が何でもその道具を使わなきゃならないという固定観念が植え付けられてしまってはいないだろうか。
<かず子>確かにそうですね。庭の木を切るのだって、種類によって、剪定バサミ、鋸、チェーンソー、と使い分けるわね。
<先 生>では、この場合の問題は何を使えばいいかということだけど、もともとの図形は「平行四辺形」という特別な形だよね。ベクトルは任意の図形の性質に対してその本領を発揮するわけだから、平行四辺形で使うには大げさすぎないだろうか。「平行四辺形の問題は初等幾何で」というのが先生の持論なんだ。
<よしお>いわれてみればそうですよね。もちろん、ベクトルでも解けるっていうひとつの演習とみてやることは必要かもしれませんが、いつもベクトルで解くのはすごい回り道をしていることになりますよね。
<先 生>その通り。では、次の問題をやってごらん。
ex) 平行四辺形ABCDにおいて、辺BCの中点をE、辺CDを2:1の比に内分する点をF、辺ADを1:3の比に内分する点をGとし、線分EGと線分BFの交点をPとする。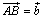 , ,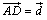 として、次の問いに答えよ。 として、次の問いに答えよ。(1) 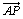 を、 を、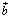 , ,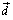 で表せ。 で表せ。(2) 比GP:PEを求めよ。 |
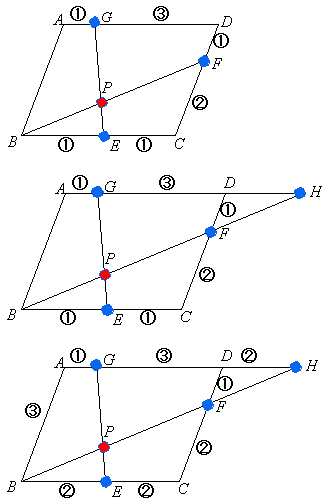 <かず子>これも一見するとベクトルでやれって要求しているような問題ですね。でも先生がいったように平行四辺形の問題だから比の関係から考えるってことですよね。まず、図を描いてみると右のようになります。でもこのあとどうすればいいんだろう。
<かず子>これも一見するとベクトルでやれって要求しているような問題ですね。でも先生がいったように平行四辺形の問題だから比の関係から考えるってことですよね。まず、図を描いてみると右のようになります。でもこのあとどうすればいいんだろう。
<まなぶ>うーん、相似な三角形がさっきのように作れないから僕にもちょっとわからないや。先生、ラクに考えようと思ったって、相似がわからなきゃベクトルでやった方が速いんじゃないですか。
<先 生>幾何の醍醐味は補助線一本で世界が変わるってことだ。その補助線もけっして奇抜な発想から生まれるものではない。この場合は、相似を見つけられないのなら、相似になるような三角形を補助線で作ってやればいいんだ。
<よしお>………、あっ、そうか。BFを延長するんですね。
<まなぶ>僕も分ったぞ。ADとBFの延長線の交点をHとして、三角形を作るんだ。そうすると相似な三角形がいくつかできますよね。
<かず子>そうすると、いまの場合GPとPEの比を求めるのだから、そうか、△PBEと△PHGが相似であることを利用するんですね。
GP:PE=GH:BE
だから、あとはGHとBEの比だけど……、うーんと、これは…。
<まなぶ>かず子、他の三角形の相似関係を使えばいいよ。例えば、
△FBC∽△FHDだから、BC:DH=CF:FD=2:1
ここで平行四辺形が特別な形であることの威力が発揮されますね。
AD=BCで、ADは4等分を基準にしているから、
AD:DH=4:2
以上より、
GP:PE=GH:BE=5:2
(2)ができちゃいました。
<よしお>そうすると(1)は、
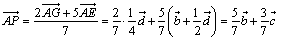
となります。
<先 生>そうだね。でも、もう少し簡単にできるよ。だって、
BP:PH=BE:GH=2:5
だろう。ここで、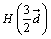 だから、
だから、
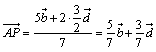
となる。では、ついでにBP:PFはどうなるだろうか。求めてごらん。
<かず子>いま先生がいった相似比が使えると思うわ。
BP:PH=BE:GH=2:5
それと、
BF:FH=BC:DH=2:1
ここで、点P,Fはどちらも線分BH上の内分点で、それぞれ全体を7,3の長さとみたときの比だから、最小公倍数の21の長さに揃えると
BP:PH=6:15
BF:FH=14:7
とすると、
BP:PF=BP:(BF-BP)=6:8=3:4
となります。
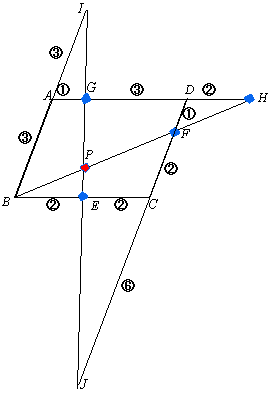 <よしお>あるいは、先生が教えてくれたような補助線を考えてもいいんじゃないかな。四角形ABEGやGECDの欠けている部分を補って三角形を作ると、右図のようになります。
<よしお>あるいは、先生が教えてくれたような補助線を考えてもいいんじゃないかな。四角形ABEGやGECDの欠けている部分を補って三角形を作ると、右図のようになります。
△IAG∽△IBEだから、
IB:AB=BE:AG=2:1 より IA:AB=1:1
△JDG∽△JCEだから、
GD:EC=JD:JC=3:2 より JC:CD=2:1
したがって全体の長さを揃えると、
BP:PF=BI:JF=6:8=3:4
となる。
<まなぶ>うーん、確かによしおの方法で求められるけど、かえって面倒になってしまっているんじゃないかな。かず子のやり方の方がスマートだと思うな。あるいは、僕的にはここでベクトルを使ったっていいんではないだろうか。
Fの座標は、
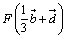
だろ。そうすると、
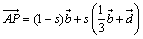
そして、先ほどよしおが求めた
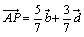
の式で を比較すると、s=3/7がすぐ分るだろう。したがって
BP:PF=3:4
ほら、簡単に求められた。
<先 生>三者三様の方法が示されたね。
先生がいいたかったのは「簡単な問題は簡単に解こう」ということだ。
平行四辺形という特別な四角形であれば、わざわざベクトルという道具を持ち出すのは大げさすぎるから、幾何の相似比という道具を使えば簡単に求められる。
でも、平行四辺形上の辺の分点が増えてしまうと分割される図形が多くなりすぎて、今度は相似比という道具では処理し難くなってしまうこともある。先ほどの後半の問題がそうだろう。
そのときに、また再び道具箱の中から一番いい道具を取り出せるかということが大切なんだ。例えば(2)の問題が ではなく、BP:PFの方を要求していたとしたら、果たしてみんなはどの道具を最初にとりだしたろうか。
そういった意味では、先読み、深読み、思い込みに秀でているまなぶが一番良く道具を使いこなしていたのではないかと思うな。
<まなぶ>先生。先生は、洞察、熟慮、深慮といった言葉をひょっとしたら知らないんじゃないですか。
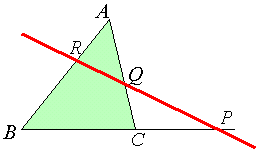 《メネラウスの定理》
《メネラウスの定理》
ある直線が△ABCの辺BC,CA,ABまたはその延長と交わる点をそれぞれP,Q,Rとすると、 |
バランスの妙を感じさせる定理であり、ここから多くの定理が派生します。
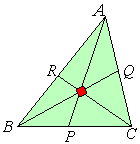 《チェバの定理》
《チェバの定理》
△ABCの3辺BC,CA,AB上にそれぞれ点P,Q,Rがあり、3直線AP,BQ,CRが1点で交われば、 |
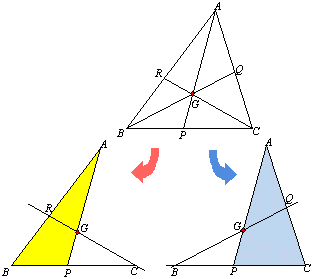 メネラウスの定理から導かれる代表的な定理です。
メネラウスの定理から導かれる代表的な定理です。
△ABPに直線RGが横切るとみると、メネラウスの定理より、
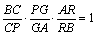
次に、△AOCに直線QGが横切るとみると、
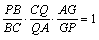
この2式を辺々掛けることで、チェバの定理が得られます。
そして、これらの定理はその逆も成立します。
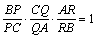
とします。
このとき、P,Q,Rが△ABCの辺BC,CA,ABまたは延長の点であれば、3点は一直線上にあります。(メネラウスの逆)
P,Q,Rが辺BC,CA,AB上の点であれば、線分AP,BQ,CRは1点で交わります。(チェバの逆)
この定理の性質をベクトルで読み替えれば、ベクトルの一次独立や共線問題、共点問題が簡単に片付けられてしまうことが分ります。
ところで、メネラウスの定理は任意の多角形においても成立します。
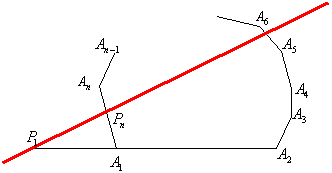 《多角形におけるメネラウスの定理》
《多角形におけるメネラウスの定理》
n角形A1A2A3……An-1Anのどの頂点も通らない直線 が、辺AkAk+1 (k=1,2,3,…,n ただしAn+1=An)またはその延長と交わる点をPkとするとき、 |
この定理は帰納法により簡単に証明できます。
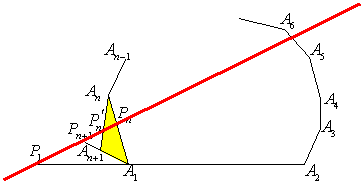 辺AnA1の間に頂点An+1をとり、凸(n+1)角形を作ります。
辺AnA1の間に頂点An+1をとり、凸(n+1)角形を作ります。
直線lが、辺AnAn+1,An+1A1またはその延長と交わる点をそれぞれPn',Pn+1とし、△AnAn+1A1にメネラウスの定理を使うと、
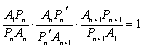
ここで、n角形で成立すると仮定すると
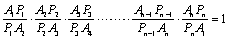
二式を辺々かけて、
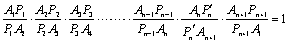
最後にPn=Pn'と置き換えると、(n+1)角形で成立することが示されます。
このようにメネラウスの定理は任意の多角形で成立しています(ちなみにチェバの定理は任意の奇数辺の多角形で成立します)が、図形問題で相似比を考える場合の補助線は、メネラウスの定理が利用されるように引かれることが多いようです。
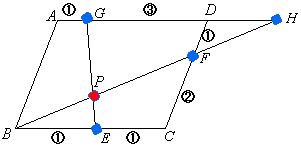 例えば、本文中の右図の補助線は、四角形GECDに直線BFが横切ると考えると、
例えば、本文中の右図の補助線は、四角形GECDに直線BFが横切ると考えると、
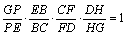
であり、辺GDの延長と直線BFとの交点である点Hの必然性が生まれてくることになります。
補助線は、暗に間接的に定理の利用を示唆するわけで、そう考えると「発想」的補助線はそれほどないことが分るでしょう。
話を元に戻しましょう。
幾何が教育数学から姿を消そうとしています。新指導要領においても、義務教育の3割削減の最大の被害を被ったのは幾何でした。ゆとりと遊びの微妙な兼ね合いで実践された現行教育課程は学力低下というお荷物を残して姿を消しますが、新教育課程は、本来成長期において培い、育てるはずである、まなぶがいう「塾考、洞察」の機会を義務教育から奪い、浸蝕を始めました。
平行四辺形に特別な感情を抱くことは無意味である、そんな時代が到来するのかもしれません。
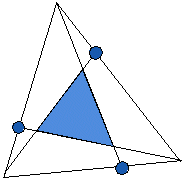 メネラウスの定理の美しさを味わえる問題
メネラウスの定理の美しさを味わえる問題三角形の3頂点とその対辺を2:1に内分する点を結ぶ線分によって囲まれてできる三角形の面積はもとの三角形の面積の何倍か。
|