| ex) 次の放物線と直線で囲まれた図形の面積を求めよ。 (1) y=2x2-x-1，x軸 (2) y=2x2-x，y=2x-1 (3) y=(x-1)2/2，x=4， x軸 (4) y=2x2-3x+4，x軸，x=-1，x=3 |
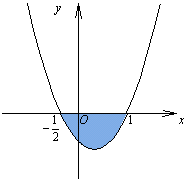＜かず子＞(1)は、放物線とx軸との交点が、(-1/2，0)，(1，0) だから、面積Ｓは、
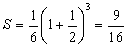
＜よしお＞かず子、グラフの開きを忘れているよ。その計算は開きが1の場合だろ!!。
＜かず子＞そうだったわ。この場合のグラフの開きは2だから、
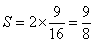
ですね。
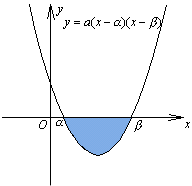＜先 生＞ 公式を確認しよう。放物線 y=a(x-α)(x-β)とx軸で囲まれる図形の面積は、
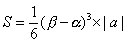
で求められるんだったね。
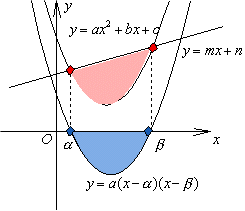＜よしお＞じゃ、(2)は僕がやります。放物線と直線で囲まれた図形をy軸に平行にスライスしてx軸上に落とします。これから、求める図形の面積は、放物線 y=2x2-3x+1とx軸で囲まれた部分の面積と同じになります。x軸との交点は(1/2，0)，(1，0)ですから、求める面積は、
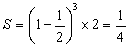
となります。
＜先 生＞快調だね。次はまなぶの番だね。
＜まなぶ＞えーっと、(3)ですね。これって、元祖ストリーキングのアルイタデスとかなんとかいった人が考えた面積ですよね。
＜かず子＞アルキメデスよ、覚えておきなさいよ。
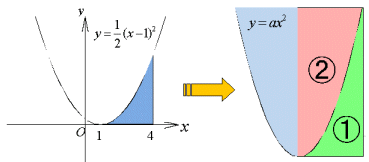＜まなぷ＞そうそう、それ。右図の面積比は、確か２：１になると思ったけど。
＜先 生＞その通り。まなぶにしては珍しく物覚えがいいね。
＜まなぶ＞先生、「珍しく」は余計だよ。先に進みます。結局、長方形の面積が 27/2 だから、求める面積は、
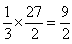
となります。
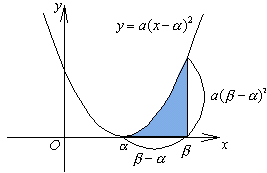＜先 生＞これも、復習しておこう。放物線 y=a(x-α)2とx軸および直線y=βで囲まれる図形の面積Ｓは、２辺の長さが ｜β-α｜、｜a｜(β-α)2 である長方形の 1/3 倍より、
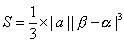
で得られるね。さあ、では最後の問題だ。誰か、解いてごらん。
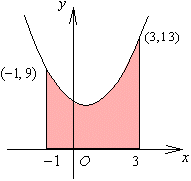＜かず子＞これは、単純に積分を計算するしかないですよね。
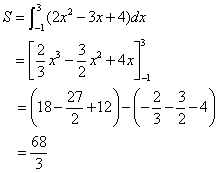
となります。
＜先 生＞まあ、とりあえずはそれで答えがでたね。
＜よしお＞とりあえずっていうのはどういうことでしょう。
＜まなぶ＞また、先生の蛇のようにしつこい考え方だよ。(1)から(3)までの問題がみな放物線の性質を利用して面積を求めているだろ。だから、この問題もそのやり方で解けってことさ。
＜先 生＞まなぶ。けんかを売っているのかな。まなぶに指摘されたのは本意でないけどその通りだ。単純に積分計算をするのではなく、図形上の性質を使ってこの面積を求めることはできないだろうか。
＜生徒達＞？？？？
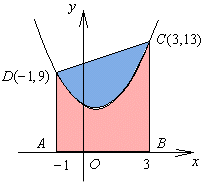＜よしお＞はい、(1)の方法を使うと求めることはできると思います。図の台形ABCDの面積 Ｓ1から、放物線と線分CDとで囲まれる図形の面積Ｓ2を引けばいいんです。
まず Ｓ1 ですが、台形の上底、下底の長さがそれぞれ 9，13 で、高さが4 だから、
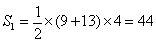
次に
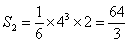
以上から、求める面積Sは、
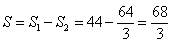
となります。
＜かず子＞うーん。確かに求められると思うけど、でもその方法じゃ、単純に計算するのと煩雑さは大して変わらないと思うわ。だっと、放物線の両端のy座標を求めなくちゃならないんでしょ。
＜まなぶ＞それに、オレ的には、面積の引き算って部分も嫌だな。
＜-先 生＞では、２人の意見を尊重して、その方向でもう少し考えてみようか。まず、まなぶのいった面積の差は計算し難いってことだから、差ではなく和で考えてみたらどうだろうか。
＜よしお＞和ですか。求める面積を分割すればいいってことですよね。縦に割ったって意味ないし……。
＜まなぶ＞………分かった。先生、接線を引くのでしょう。
＜かず子＞接線ってどんな接線？。
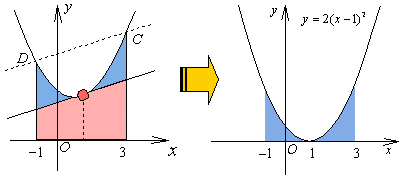＜まなぶ＞線分CDに平行な放物線の接線だよ。右図のように面積を分けるんだ。
＜かず子＞でも、その接点はどうやって求めるわけ。
＜よしお＞接線と放物線で囲まれた図形を縦にスライスしてx軸上に落としたらどうだろうか。すると、右下図のようになるよね。
＜まなぶ＞そうすると接点は両端のx座標であるx=-1，x=3 の中点ってことだ。だから、接点のx座標は、x=1 ってことになる。その面積 Ｓ1は、
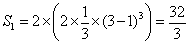
あとは残りの台形の面積 を求めればいいんだ。
＜かず子＞でもそれが難しいんじゃないの。
＜先 生＞ヒントだ。台形の面積は、
で得られるけど、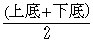
は数学的にはどういう意味をもっているだろう。
＜よしお＞足して２で割っている分けだから、平均ですね。あっ、そうか、x=-1 と x=3 における高さの平均だから、その中点 x=1 の高さに等しいということですね。だから、x=1 における放物線のy座標の値を求めればいいわけだ。
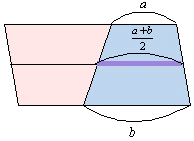＜先 生＞その通り。右図を見るとそのことは明らかだよね。
ではその面積 Ｓ2 を求めてご覧。
＜まなぶ＞はい。x=1 のときのy座標は、y=3 だから、
Ｓ2=3×4=12
です。そうすると、求める面積Ｓは、
Ｓ=Ｓ1+Ｓ2=32/2+12=68/3
先生、求まりました。
＜先 生＞その通り。この方法だと、求めなければならない放物線のy座標は、１つでいいことになり、かず子が前の解き方で指摘してした２つも求めなければならない煩雑さも解消できたことになるね。
＜かず子＞なんか今日のまなぶって冴えてるね。
＜まなぶ＞今日は、能ある鷹の爪をちょっとだしすぎちゃったかなあ。
＜先 生＞でも、接線を引くというアイデアはどうしてでてきたんだい。
＜まなぶ＞簡単ですよ。だって、それって問題(3)のやり方でしょ。先生のいつもの性格なら、最後の問題は必ずそれまでの問題を応用した形にすると踏んだんです。放物線の性質を考えるより、先生の性格を考えたほうが、ずっと単純で、理解し易いと思いませんか。
＜先 生＞………
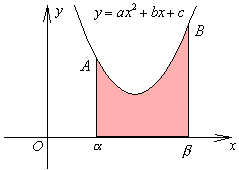今回の面積の求め方をまとめてみましょう。
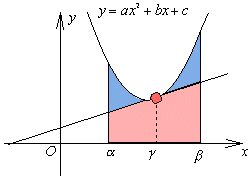直線ABに平行な接線で、面積を上下に２つの図形に分けると上部の図形の面積 Ｓ1は、接点のx座標が x=(α+β)/2より、
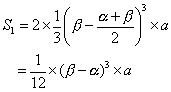
となります。次に下部の台形の面積 Ｓ2は、
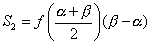
で得られます。以上より、
………(＊)
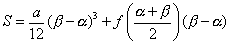となります。
| ex)放物線 f(x)=3x2+2x+1, x軸、x=-4、x=2 で囲まれる図形の面積を求めよ。 |
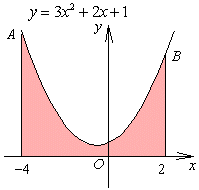右図において、中点のx座標は x=-1で、f(-1)=2 より面積Ｓは、
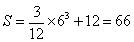
となります。
なお、公式(＊)は、上に凸の放物線においても成立します。
この場合は、a＜0 となり、台形の面積から接線と放物線で囲む面積を減じることになります。
| ex)放物線 f(x)=-x2+4x+6、x軸、x=1、x=5 で囲まれる図形の面積を求めよ。 |
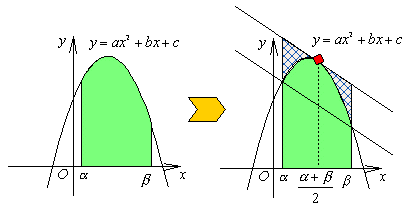中点のx座標は x=3で、f(3)=9 より面積Ｓは、
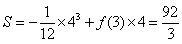
となります。
ところで、今回の小手技では、まなぶが妙に冴えたところを見せています。
いままで随分、先生やかず子に苛められて、虐げられてきたまなぶですが(当の本人はそんなことは毛ほども感じてはいないのですが)、今回は要所、要所にうまく立ち回り、最後は先生をやり込めてしまいます。
よく会話を読むと、結局は大事な計算の部分はよしおにさり気なく振っていて、要領のよさも、エスカレートしています。
一味変わったまなぶは、これからどう小手技に絡んでくるのでしょう。
そして、かず子との関係は………。
２００１年は、まなぶが逆襲します。