札幌新川高等学校　中村文則

＜先　生＞ 前時は，二次方程式の解は，次のようにグラフ化することで，放物線とx軸との交点のx座標になることを学んだよね。
　　
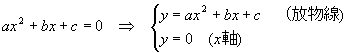
となる。さあ，今日はこの考えを発展させて，二次不等式の解法に挑戦してみよう。二次不等式も次のようにグラフ化できます。
　　
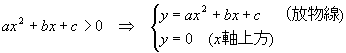
　これから，この二次不等式は，放物線でx軸上方の領域にある部分を表しているわけだ。例題で考えてみよう。

＜まなぶ＞標準形に変形し，頂点と軸を求めます。

＜先　生＞そうだね。でもこの問題で必要なのは，グラフとx軸の関係だけなんだ。x²の係数＞0から，下に凸の放物線であることは既に分かっている。x軸との関係はどうやって調べればいいかな。

＜かず子＞はい，三種の神器の１つ，判別式です。D＝16−4＞0ですから，x軸と2点で交わります。

＜先　生＞そうだね。このとき，x軸上方にある放物線上の点のx座標の取り得る値の範囲を不等式の解というんだ。x軸上にその範囲を図示してご覧。（手が動かない生徒，y＜0の範囲を図示している生徒がいるのを確認してから）

＜先　生＞うーん，ではちょっとみんなにイメージを与えてあげよう。

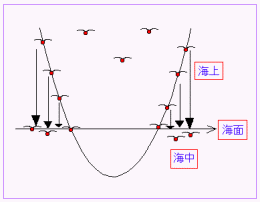
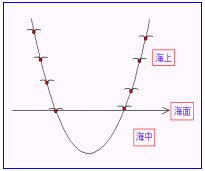　積丹の神威岬にいったことあるかい。ない？，なければどこか適当な岬でいいから思い浮かべてごらん。君は恋人と手をつないで展望台に立っているんだ。エメラルドブルーの海を恋人と眺めている。彼方に空と海が出会うところが地平線だ。これをx軸に見立ててやろう。その地平線の上方をカモメが飛ぶ。君達のようにお互い寄り添いカモメ達は編隊飛行をしている。その様は下に凸の放物線とオーバーラップするね。彼らは編隊を組みながら餌を取りに海に近いものから順に海中に飛び込む。その状態が(1)のグラフだ。
　どうだい，イメージはできたかな。すなわち，x軸（y＝0）を表す水平線，分かりやすく海面と言おう，これを境にして，y＞0が上空，y＜0が海中ということだ。このとき(1)の不等式はまだ上空を飛んでいるカモメはどれだけかということを要求していることになる。そこで，対象となっているカモメ達を海面に浮かべてみよう。カモメだって疲れるんだ。いつまでも飛んではいられない。
　さあ，またイメージだ。フワッとカモメ達は海面に降り立つ。潜っているカモメ達を挟んでその両脇にカモメ達が整列する様が思い浮かぶかな。これが，求めるカモメすなわちxの存在する範囲だ。では，この範囲を求めてみよう。まず，端のカモメを表すxの値を求める，かず子，計算してごらん。

＜かず子＞y=0のときですから，方程式x²−4x+1=0の解を，三種の神器の解の公式で求めて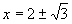，です。

＜先　生＞これで，不等式を表す数の基準が作られた。あとは，範囲内にある適当なカモメをxにして，不等号「＜」でつなげばよい。

　　　
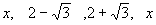
の順だから，解は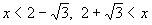，となる。
　いいかな，数は小さい順から「＜」で結んでいくんだよ。

　では，(2)を各自，解いてごらん。（…演習…），まなぶ，出来たかい。

＜まなぶ＞はい，まず，判別式からx軸と2点で交わる下に凸の放物線になります。x軸との交点のx座標はまだ計算の途中なんですが。

＜先　生＞まなぶ，君は解の公式を使っているのかな。

＜まなぶ＞はい，そうですが，まずいんですか……あっ，因数分解できる。えーと，y＝(x−1)(x−2)だからx座標は，1と2です。

＜先　生＞ＯK！，さあ次はどこにいるカモメを求めるかということだけど，かず子，どうだろう。

＜かず子＞　y≦0だから，海面と海中のカモメです。

＜先　生＞そうだね。等号があるから海面のカモメも要求していることを忘れないようにしよう。あとは，潜っているカモメを海面に浮かび上がらせればいい。潜ってりゃ，息が苦しくなって上がって来るもんだ。適当なカモメをxとして，1，x，2の順に不等号で結んで，解は，1≦x≦2となる。
　今度は，(3)だ。まず，カモメはどこにいるだろう，かず子。

＜かず子＞D＝9−16＜0より，下に凸だから，みんな空を飛んでいます。

＜先　生＞では，解を表すカモメはどう表現できる。

＜かず子＞「y＞0」は，空を飛んでいるカモメを聞いているんだから……。

＜先　生＞別に不等式の解にこだわる必要はないよ。自分の言葉として表現してごらん。

＜かず子＞はい，「ぜんぶのカモメ」です。

＜先　生＞そう，それでいい。すべてのカモメが海面に降り立つ訳だから，その様をイメージすればいいわけだ。ズラーッと横一直線に並ぶ様子は，壮観というか，不気味というか……ヒチコックの「鳥」を思い出させるね(生徒無反応，うけない)。
　さて，この解を「すべての数」と表現することにしよう。カモメが数なわけだ。反対にまったくカモメがいない場合を「解はない」というんだ。では最後に，(4)を求めよう。まなぶ，やってごらん。

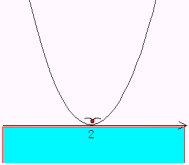
＜まなぶ＞D＝0より，x軸と1点で交わるから，x軸に放物線は接しています。

＜先　生＞接点のx座標はなんだい。

＜かずお＞因数分解して，x=2です。で，y≦0だから，海中と海面のカモメを探して……2のカモメしかいません。

＜先　生＞うん，「2のカモメ」，最高の表現だ。したがって，x＝2が答えとなる。
　確かに，数字の2はなんとなく海面を漂うカモメに似て見えるよね。