

ex) 三角形ABCの内部の点Pが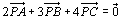 を満たしているとき、次の問いに答えよ。 (1) 線分APの延長が辺BCと交わる点をDとするとき、BD:DCおよび、AP:PDを求めよ。 (2) △PBC:△PCA:△PABを求めよ。 |
<先 生>図形問題をベクトルで解決するにはまず始点を決めることから始めるんだったね。どこに始点を設定すればいいだろう。
<よしお>平面上の適当な場所に、点Oを決めます。
<かず子>あるいは三角形の頂点の1つを始点にします。
<先 生>そうだったね。でも今日の授業ではそれ以外の始点を考えてみようか。他に何処を始点にすればいいと思う。
<生徒達>………
<先 生>迷うことなんてないんじゃないかな。だって問題文で与えられている点は限られているんだから。
<まなぶ>……まさか点Pですか。
<先 生>正解。でもどうして「まさか」なんだい。
<まなぶ>だって、点Pは求める点ですよね。まだ分かっていない点を始点にするのはなんか釈然としないのですが。
<先 生>でもね。先ほどよしおは始点を原点Oにすれば、ということをいってたね。じゃあ、その原点はどこにあるかっていったら答えられないだろう。点Pだって同じだろ。それに問題文をよくみてごらん。既に点Pを始点として表現されているじゃないか。だったらそれを使えばいいわけで、新たに始点を設定する必要性はないのではないだろうか。とにかくやってみようか。条件式より、
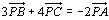
さあ、ここで、左辺をみてごらん。分点の公式を考えると左辺の分母になにがあると都合がいいだろうか。
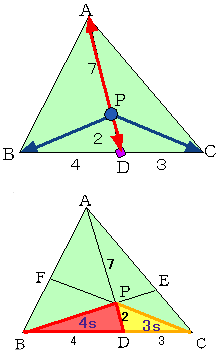 <よしお> 3+4=7です。そうすると、
<よしお> 3+4=7です。そうすると、
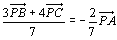
となり、右辺は線分BCを4:3の比に内分する点を表しています。
<先 生>そうだね。その点をDとしようか。すると、
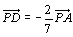
この式の右辺から点Pはどこにあるか考えてごらん。
<かず子>点Pから反対方向に2つの点A,Dがあり、その長さがPA=7とすると、PD=2ですよね。
<先 生>そうだね。これでもう問題(1)が求められていることが分かるかな。まとめよう。
点Pは、線分BCを4:3の比に内分する点Dに対して、線分ADを7:2の比に内分する点である。
ということだね。
<まなぶ>凄い。めっちゃ簡単にでちゃった。何か不思議ですよね。
<先 生>不思議でもなんでもないよ。さきほどいったように、点Pを始点とみるのが自然で、それ以外に始点を設定する方が不自然ではないだろうか。では後半(2)だ。さあ、どうするんだっけ。
<かず子>点Dによって、三角形PBCは三角形PBDと三角形PDCに分割されますが、それぞれの面積比は、底辺BDとDCの長さの比に等しいことを利用します。
この場合BD:DC=4:3ですから、△PBD=4s,△PDC=3sとおけます。
次に、△PAB:△PBD=AP:PD=7:2だから、えーっと、△PBD=4sなんだから、……、あのー、△PBD=8sにして、もう一回やっていいですか。
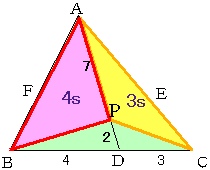 <先 生>いや、もういいよ。みんなもやり方はいいね。結局分割された1つの三角形の面積sを基準にして他の面積をsで表せばいいということだな。かず子はなるべ値が分数にならないように数値合わせに苦労していたみたいだけどね。でもね、もう一度よく図形をみてごらん。いま、BD:DC=4:3だったね。では△PABと△PCAの面積比はなんだろう。
<先 生>いや、もういいよ。みんなもやり方はいいね。結局分割された1つの三角形の面積sを基準にして他の面積をsで表せばいいということだな。かず子はなるべ値が分数にならないように数値合わせに苦労していたみたいだけどね。でもね、もう一度よく図形をみてごらん。いま、BD:DC=4:3だったね。では△PABと△PCAの面積比はなんだろう。
<まなぶ>うーん、△ABDと△ADCなら底辺BDとDCの比と同じだから4:3なんだけどな。
<かず子>あっ、そうか。△PABと△PCAの比も4:3だわ。
<まなぶ>どうしてだい。
<かず子>だって、まなぶのいってた三角形から△PBDと△PDCを引いたものが、△PABと△PCAでしょ。引く三角形の面積比も4:3なんだから、△PABと△PCAの面積比だって変わらないわ。
<先 生>結論がでたね。では△PCAの面積はどうなるだろう。
<まなぶ>まず△PABと△PBDの面積比は底辺APとPDの比と同じだから7:2です。だから、△PAB=7sとおくと、△PBD=2s,次にBD:DC=4:3なんだから……。
<先 生>おいおい、それじゃさっきのかず子の計算と同じようなことをしているよ。△PBC=△PBD+△PDCだ。ここで、△PABと△PBDの面積比はAPとPDの比と一致する。△PCAと△PDCについても同じだね。そうすると、△PAB+△PCAと、△PBCの面積比はどうなる。
<まなぶ>そうか。やっぱり、APとPDの面積比に一致します。そうすると、△PAB+△PCA=4+3=7とみれば、あれ、AP:PD=7:2だからうまくできますね。△PBC=2です。ラッキーですね。
<先 生>実は偶然でもなんでもないんだ。これは当然そうならなければいけないんだ。もう少し、別の見方をしてみようか。問題文を今度は、
としてみよう。もうみんなはこれからBPの延長が辺CAをどのように分けるか分かるね。
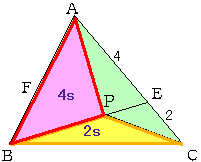 <かず子>はい。交点をEとすれは、CE:EA=2:4 です。
<かず子>はい。交点をEとすれは、CE:EA=2:4 です。
<先 生>これは1:2だけど、2:4のままにしておこう。すると、△PBC:△PAB=2:4とだせるんだったね。ところで△PAB:△PCA=4:3だったんだから、
△PBC:△PCA:△PAB=2:3:4
<まなぶ>へーっ、不思議だ。これもきれいに求められている。
<先 生>なんでもいうけど、不思議でもなんでもない。至極当たり前のこれは結果なんだ。
<まなぶ>先生、そろそろ種明かしをしてよ。
<先 生>その前にもうひとつ質問。この面積比の数字をみて何か気が付くことはないだろうか。
<よしお>僕も気になっていたんですけど、問題文の式のベクトルの係数に一致してますよね。
<まなぶ>ほんとだ。ミステリーだ。
<先 生>くどいようだけど、不思議でも何でもない。まなぶがうるさいから種明かしに移ろう。まず、下準備として、次の問題を考えてみよう。
ex) 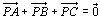 を満たす△ABCの内部の点Pを求めよ。 を満たす△ABCの内部の点Pを求めよ。 |
<かず子>先ほどと同様にして……
<先 生>そんな必要はないよ。ちょっと始点をOに変えてみてごらん。
<かず子> 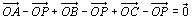 だから、
だから、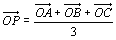 。なんだ、点Pは三角形ABCの重心ですね。
。なんだ、点Pは三角形ABCの重心ですね。
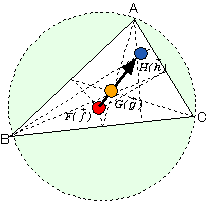
<先 生>一般に、三角形の重心をGとすると、
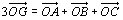
なる大事な関係が成り立つ。ここで、始点OをGに移してやると、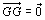 だから、
だから、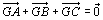 となるわけだ。
となるわけだ。
ところで、Pが三角形の重心であるならば、APとBCとの交点をDとすると、AP:PD,BD:DCは簡単だよね。
<まなぶ>DはBCの中点だから、BD:DC=1:1,AP:PD=2:1です。
<先 生>では、△PBC:△PCA:△PABを求めるとどうなる。
<よしお>重心は中線の交点だから、先ほどの考え方を使うと、3つの三角形の面積は等しくなります。
<先 生>これから当たり前の結果がでる。三角形の内部の点が重心であるとき、その点で、三角形は面積の等しい3つの三角形に分割されるということだ。面積が重さに比例すると考えれば、重心とは三角形が内部で釣り合う点ということになる。
<まなぶ>なんか、当たり前のような、そうでないような。
 <先 生>話を続けるよ。さて、いま釣り合うといったけど、三角形上ではこれは別の見方ができる。三角形の各頂点に、同じ重さをぶらざけたとき、釣り合う点を重心ともいうんだ。
<先 生>話を続けるよ。さて、いま釣り合うといったけど、三角形上ではこれは別の見方ができる。三角形の各頂点に、同じ重さをぶらざけたとき、釣り合う点を重心ともいうんだ。
<まなぶ>頭が痛くなってきた。
<先 生>まなぶのために実際に示したほうがいいだろう。さあ、いま、図の三角形の頂点に同じ重さ1gを乗せてみよう。みんなは理科の時間に力のモーメントを学んだろ。ここで、線分ABについて、釣り合う支点を求めてやる。どこだろう。
<まなぶ>もちろん中点です。
<先 生>その点をDとしよう。このDにかかる重さは当然、両端の重さの合計2gだ。では、次に、線分ADで、釣り合いをとってみよう。そのときの支点はどこだろう。
<よしお>今度は、点Aに1g、点Dに2gの重さがかかっているんだから、線分ADを2:1の比に内分する点で釣り合います。あっ、その支点が重心Gなんですね。
<先 生>その通り。このように各辺の両端にかかる重さのバランスをとっていけば重心の性質が簡単に導かれね。それじゃ、本題だ。では、今日、最初にみんなに提示した問題のベクトルの関係式は何を意味している。
<生徒達>………
<まなぶ>ひょっとしたら、ベクトルの頭にくっついている係数は、その位置ベクトルを表す頂点の重さですか。
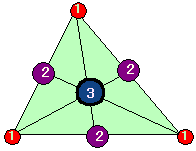
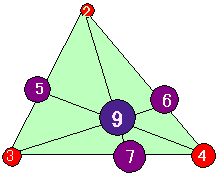
<先 生>大正解だ。ちょっと図に書いてみよう。各頂点に係数に相当する重さをぶら下げよう。点Aには2g、点Bには3g、点Cには4gということだ。さて、バランスをとっていこう。かず子やってごらん。
<かず子>はい。まず、辺BCですが、B,Cに3g,4g乗っかっているから、支点をDとすると、BD:DC=4:3、このとき支点Dには7gの重さが加わります。次に、AD上で釣り合いをとると、Aに2g,Dに7gより、ADを7:2の比に内分する点で釣り合います。その点がPということですね。
<まなぶ>不思議だ。ほんとうに求まってしまった。
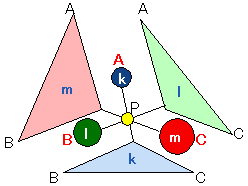
<先 生>もうわかっただろうか。一般に、
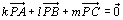
という式は、各頂点A,B,Cにそれぞれk,l,mの重さを乗せたときに三角形が点Pで釣り合っているということだ。右辺の が釣り合いを示していることになる。重心を各頂点の平均値と考えると、このように頂点に重みをつけた重心のことを荷重平均といい、その重心を質量中心というんだ。
さて、問題の後半の面積比だ。先ほど、面積は重さに比例するといった。いま各頂点に加わっている重さを面積でつり合わせてみよう。例えば、点Aと△PBCが釣り合うとみる。そうすると、△PBCの面積は、点Pにかかる重さkとみればいい。同様に残りの頂点B,Cについて考えれば、
△PBC:△PCA:△PAB=k:l:m
が得られる。
<まなぶ>はーっ、幾何学の真髄、神秘性に触れたような。ファンタジックだなあ。
<かず子>同感だわ。底が知れているまなぶがいうと、余計底の深さを感じて感動ものだわ。
 これは、三角形の内部の点のみならず、外部の点でも同様です。
これは、三角形の内部の点のみならず、外部の点でも同様です。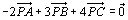
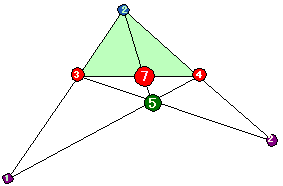
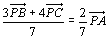 とみれば、線分BCを4:3の比に内分する点をDとすると、
とみれば、線分BCを4:3の比に内分する点をDとすると、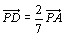 より点Pは7:2の比に外分する点です。よって、重さ−2は外分点と考えればいいわけです。
より点Pは7:2の比に外分する点です。よって、重さ−2は外分点と考えればいいわけです。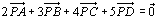
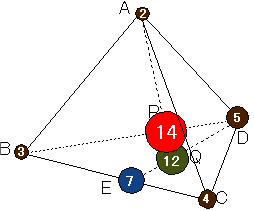 大ざっばにみれば、三角形BCDの質量中心をQとすると、Qには、頂点B,C,Dのおもりの合計3+4+5=12が加わっているわけですから、点Pの重さが2gであることより、線分AQを12:2=6:1の比に内分する点がPとなります。
大ざっばにみれば、三角形BCDの質量中心をQとすると、Qには、頂点B,C,Dのおもりの合計3+4+5=12が加わっているわけですから、点Pの重さが2gであることより、線分AQを12:2=6:1の比に内分する点がPとなります。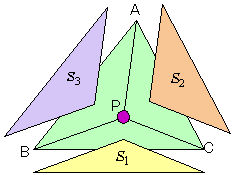 本文の結論は、各頂点A,B,Cに乗せた重みは、点Pと対辺が作る三角形の面積に比例するというものでした。
本文の結論は、各頂点A,B,Cに乗せた重みは、点Pと対辺が作る三角形の面積に比例するというものでした。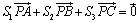
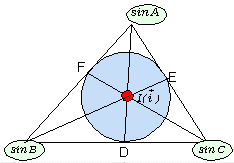 すなわち、AB=c,BC=a,CA=b、各頂点の位置ベクトルを
すなわち、AB=c,BC=a,CA=b、各頂点の位置ベクトルを 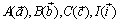 とすれば、
とすれば、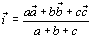
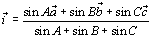
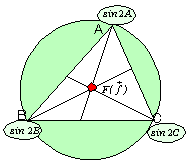 まず、外心
まず、外心 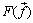 ですが、外接円の半径をrとすると、
ですが、外接円の半径をrとすると、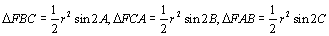
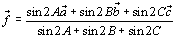
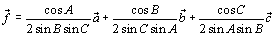
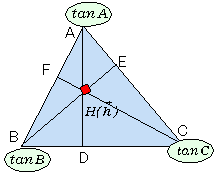 次に、垂心
次に、垂心 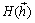 ですが、線分AHの延長と辺BCとの交点をDとすると、
ですが、線分AHの延長と辺BCとの交点をDとすると、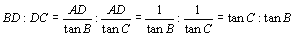
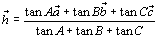
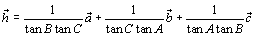
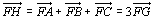
 線分FHを1:2の比に内分した点の位置ベクトルを求めます。
線分FHを1:2の比に内分した点の位置ベクトルを求めます。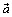 だけ考えれば十分でしょう。
だけ考えれば十分でしょう。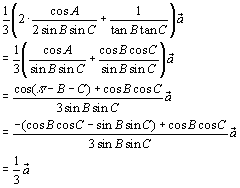
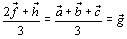
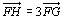 が得られます。
が得られます。