亙傑側傇亜傗偭傁傝俀偺攞悢偱偡丅
亙傛偟偍亜俁偺攞悢傕娷傫偱偄傞偲巚偄傑偡丅
亙愭丂惗亜偦偺捠傝丅傛偟偍偺偄偆傛偆偵俁偺攞悢傪娷傫偱偄傞偹丅偱偼偙偆傗偭偰偳傫偳傫愗傝庢傞娫妘傪墑偽偟偰偄偭偨傜偳偆側傞偩傠偆丅壓偺恾傪尒偰奺帺峫偊偰偛傜傫丅

亙偐偢巕亜暘偐傝傑偟偨丅娫妘偑俆偩偲俆偺攞悢丅娫妘偑俇偩偲俇偺攞悢偺傛偆偵乽娫妘偺攞悢乿傪娷傫偱偄傑偡丅
亙愭丂惗亜傕偭偲嬶懱揑偵偄偭偰傒傛偆丅娫妘偑値偺応崌偼値偺攞悢傪娷傫偱偄傞偲偄偆偙偲偩偹丅偲偙傠偱幚偼丄愭傎偳傑側傇偑偄偭偰偄偨偙偲傕廳梫側偙偲側傫偩丅娫妘俁偲偄偆偙偲偼丄娫妘俀傪墑偽偟偨傕偺偩偹丅偩偐傜俀偺攞悢傕娷傓偙偲偵側傞丅娫妘俆偱偼偳偆偩傠偆丅
亙傑側傇亜俀偺攞悢丄俁偺攞悢丄係偺攞悢丆俆偺攞悢傪娷傒傑偡丅
亙愭丂惗亜偟偨偑偭偰丄娫妘値偼丄倠(倠=侾丆俀丆俁丆乧乧丆値)偺攞悢傪娷傓丅偙傟偐傜娫妘値偵娷傑傟傞偡傋偰偺悢偺愊傪寁嶼偡傞偲丄俀偺攞悢丄俁偺攞悢丄乧丄値偺攞悢偺愊傪娷傓傢偗偩偐傜丄乽楢懕偡傞値屄偺惍悢偺愊乿偼丄
丂丂丂値亊(値亅1)亊(値亅2)亊(値亅3)亊乧乧乧亊俁亊俀亊侾丂丂丂乧乧乧(*)
偱妱傝偒傟傞偙偲偑暘偐傞傫偩丅
偝偰丄(*)偺寁嶼傪埑弅偟偰昞尰偟丄値!偲彂偔偙偲偵偟傛偆丅撉傒偐偨偼値偺奒忔(値 factorial) 乽傂傖偔偲偍傝偁傞乿側傫偰岅楬崌偣偱妎偊傟偽傛偄丅
亙惗搆払亜乧乧乧乧
亙愭丂惗亜乧乧傑偭丄忕択偼偝偰偍偒丄傑偲傔傞偲
丂丂丂乽楢懕偡傞値屄偺惍悢偺愊偼値両偱妱傝偒傟傞乿
偲偄偆偙偲偩偑丄師偵偙傟傪棙梡偟偨栤戣傪夝偄偰傒傛偆丅

亙愭丂惗亜傑偢(1)傪峫偊偰傒傛偆丅俁両亖俇偩偐傜丄梌幃偼楢懕偡傞俁屄偺惍悢偺愊偵側偭偰偄傟偽偄偄偙偲偑傢偐傞丅
丂丂丂値3亄俆値亖値(値2亄俆)
偲側傞偗偳丄偝偰楢懕偡傞俁屄偺惍悢偺愊傪偳偆傗偭偰嶌傟偽偄偄偩傠偆丅値傪偦偺傂偲偮偲偟偰峫偊偰傒傛偆丅
亙傛偟偍亜 値丆値亄侾丆値亄俀偱偟傚偆偐丅
亙愭丂惗亜偆傫丄偦偆偡傞偲丄梌幃偺拞偺場悢偵偼(値亄侾)(値亄俀) 偡側傢偪値2亄俁値亄俀 偑懌傝側偄偙偲偵側傞偐傜
丂丂丂(梌幃)亖値(値2亄俆)
丂丂丂丂丂丂亖値{(値亄侾)(値亄俀)亅(値2亄俁値亄俀)亄値2亄俆}
丂丂丂丂丂丂亖値{(値亄侾)(値亄俀)亅俁(値亄侾)}
丂丂丂丂丂丂亖値(値亄侾)(値亄俀)亅俁値(値亄侾)
偙偙偱丄値(値亄侾)(値亄俀)偼楢懕偡傞俁屄偺惍悢偺愊偩偐傜俇偺攞悢偲側傞丅傑偨丄値(値亄侾)偼楢懕偡傞俀屄偺惍悢偺愊偩偐傜俀偺攞悢丄偟偨偑偭偰俁値(値亄侾)偼俇偺攞悢丅傛偭偰丄埲忋傛傝梌幃偼俇偺攞悢偱偁傞偙偲偑傢偐傞丅偲偙傠偱懠偺傒傫側傕傛偟偍偲摨偠傛偆側楢懕偡傞俁偮偺惍悢傪峫偊偨偺偐側丅
亙偐偢巕亜偁偺偆丄巹偼丄値亅侾偲値偲値亄侾 傪峫偊傑偟偨丅
亙愭丂惗亜偱偼丄偐偢巕偺峫偊偨惍悢偵偮偄偰丄偳偆側傞偐寁嶼偟偰傒傛偆丅
丂丂丂(梌幃)亖値(値2亄俆)
丂丂丂丂丂丂亖値(値2亅侾亄俇)
丂丂丂丂丂丂亖(値亅侾)値(値亄侾)亄俇値
(値亅侾)値(値亄侾)偼楢懕偡傞俁屄偺惍悢偺愊偩偐傜柧傜偐偵梌幃傕俇偺攞悢偩偹丅偙偪傜偺曽偑暘偐傝堈偄偐傕偟傟側偄丅偱偼丄傑側傇偼偳偆峫偊偨偺偩傠偆丅
亙傑側傇亜偁偺偆丄傏偔偼丄値傪傕偲偵偡傞偺傪朰傟偰丄値亄侾丆値亄俀丆値亄俁偵偟偰偟傑偭偨傫偱偡偗偳丅
亙愭丂惗亜榖傪傛偔暦偄偰偄側偄偲偄偆偙偲偩偑丄偱傕娫堘偄偱偼側偄傛丅偪傚偭偲傗偭偰傒傛偆丅
丂丂丂(値亄侾)(値亄俀)(値亄俁)=値3亄俇値2亄侾侾値亄俇値
偩偐傜丄
丂丂丂 (梌幃)亖値3亄俆値
丂丂丂丂丂丂亖(値3亄俇値2亄侾侾値亄俇)亅俇値2亅俇値亅俇
丂丂丂丂丂丂亖(値亄侾)(値亄俀)(値亄俁)亅俇(値2亄値亄侾)
傎傜丄偱偒偰偟傑偭偨丅梫偼丄曽恓傪寛傔偨傜弶巙娧揙丄壗偑壗偱傕偦偺曽岦傊幃傪曄宍偡傞偭偰婥帩偪傪帩偮偙偲偩丅悢妛偼僄儗僈儞僩偩偗偱側偔偙偆偄偭偨嫮堷偝傕昁梫側傫偩丅偙傟傪嫮堷偖(Going)my way 偲偄偆丅
亙惗搆払亜乧乧乧
亙愭丂惗亜乧乧乧傑偭丄偲偵偐偔(1)偼偱偒偨偐傜丄師偼(2)丅傑偢梌幃傪場悢暘夝偟偰傒傛偆丅
丂丂丂(梌幃)亖値(値4亅侾)
丂丂丂丂丂丂亖値(値2亅侾)(値2亄侾)
丂丂丂丂丂丂亖(値亅侾)値(値亄侾)(値2亄侾) 乧乧(**)
偝偰丄偙偙偱丄(値亅侾)値(値亄侾)偼楢懕偡傞俁屄偺惍悢偺愊偩丅俆偺攞悢偱偁傞偙偲傪帵偡偵偼楢懕偡傞俆屄偺惍悢偺愊傪嶌傟偽偄偄丅偱偼巆傝偺俀偮偺惍悢偼側傫偩傠偆丅
亙傛偟偍亜 (値亄俀)丆(値亄俁)偱偡丅
亙愭丂惗亜妋偐偵偦偆偩偗偳丄傕偆彮偟寁嶼偟傗偡偄傕偺偼側偄偐側丅
亙偐偢巕亜値亅俀偲値亄俀偺傎偆偑偄偄偲巚偄傑偡丅
亙愭丂惗亜偦偆丄偦偺捠傝丅(値亅侾)値(値亄侾)偺慜屻偺悢傪峫偊傟偽偄偄偹丅偦偆偡傞偲(値亅俀)(値亅侾)値(値亄侾)(値亄俀)偲偄偆楢懕偡傞俆屄偺惍悢偺愊偑嶌傜傟傞丅偝偁丄偦傟偱偼曄宍偟傛偆丅
丂丂丂 (梌幃)亖(値亅侾)値(値亄侾){(値2亅係)亄俆}
丂丂丂丂丂丂亖(値亅俀)(値亅侾)値(値亄侾)(値亄俀)亄俆(値亅侾)値(値亄侾)
偁偲偼丄傕偆柧傜偐偩傛側丅
偲偙傠偱丄(**)傪尒偰偛傜傫丅偙偺幃偺(値亅侾)値(値亄侾)偼楢懕偡傞俁屄偺惍悢偺愊偱偁傞傢偗偩偐傜丄幚偼梌幃偼俇偺攞悢偱傕偁傞丅偟偨偑偭偰丄梌幃偼俆偺攞悢偐偮俇偺攞悢丄偡側傢偪俁侽偺攞悢偵側偭偰偄傞傫偩丅
偝偁丄偦傟偱偼嵟屻偺栤戣(3)偩丅傑側傇丄傑偢場悢暘夝傪偟偰傒傛偆丅
亙傑側傇亜 (梌幃)=値(値6亅侾)
丂丂丂丂丂丂丂丂亖値(値2亅侾)(値4亄値2亄侾)
丂丂丂丂丂丂丂丂亖(値亅侾)値(値亄侾)(値4亄値2亄侾)
偲側傝傑偡丅
亙愭丂惗亜俷俲両丅偙偺抜奒偱俇偺攞悢偱偁傞偙偲偑暘偐傞偹丅偟偨偑偭偰係俀偺攞悢偱偁傞偵偼丄偁偲偼俈偺攞悢偱偁傞偙偲傪帵偣偽傛偄丅偝偁丄偦傟偱偼楢懕偡傞俈屄偺惍悢偺愊傪嶌偭偰傒傛偆丅傛偟偍丄偳偆偡傞丅
亙傛偟偍亜丂(値亅侾)値(値亄侾)丂偺慜屻偵丄(値亅俁)丆(値亅俀)丆(値亄俀)丆(値亄俁)傪妡偗傑偡丅
亙愭丂惗亜偩偄傇丄梫椞椙偔側偭偰偒偨側丅
丂丂丂(値亅俁)(値亅俀)(値亄俀)(値亄俁)亖(値亅俁)(値亄俁)(値亅俀)(値亄俀)
丂丂丂丂丂亖(値2亅俋)(値2亅係)
丂丂丂丂丂亖値4亅侾俁値2亄俁俇
偩偐傜丄
丂丂丂(梌幃)亖(値亅侾)値(値亄侾)(値4亄値2亄侾)
丂丂丂丂丂亖(値亅侾)値(値亄侾){(値4亅侾俁値2亄俁俇)亄侾係値2亅俁俆}
丂丂丂丂丂亖(値亅俁)(値乕俀)(値亅侾)値(値亄侾)(値亄俀)(値亄俁)亄俈(俀値2亅俆)(値亅侾)値(値亄侾)
偝偁丄俈偺攞悢偱偁傞偙偲偑帵偝傟偨偹丅
丂廬棃偼丄椺偊偽俇偺攞悢傪帵偡偵偼丄忚梋宯傪峫偊俀偲俁傪朄(modulus)偲偟偰暘椶偟丄応崌暘偗偱徹柧偟偰偄偨偑丄乽悢妛嘥乿偱暲峴偟偰屄悢偺張棟傪妛傇傛偆偵側偭偰偐傜偼丄慻崌偣傪棙梡偟偨曽朄傕壜擻偲側偭偰偒偨丅
丂丂丂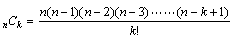
丂偙偙偱丄 偼帺慠悢偱偁傞偙偲偐傜丄塃曈傕帺慠悢丅傛偭偰丄値(値亅侾)(値亅俀)(値亅俁)乧乧乧(値亅倠亄侾)側傞楢懕偡傞倠屄偺惍悢偺愊偼倠両偱妱傝偒傟傞丅偟偨偑偭偰丄倣(俀亝倣亝倠)偺攞悢偱偁傞偐偳偆偐傪帵偡偵偼楢懕偡傞倠屄偺惍悢偺愊傪嶌傟偽偄偄偙偲偵側傞丅偦偟偰攞悢栤戣偼丄偙偺峫偊曽偺曽偑埨堈偵偦偟偰娙扨偵偱偒偰偟傑偆偙偲偑懡偄傛偆偩丅
丂傕偪傠傫応崌暘偗偲偄偆傕偭偲傕悢妛揑側巚峫惍棟朄偼戝愗偵偟側偗傟偽側傜側偄偲巚偆偑丄拞妛峑偱偺応崌暘偗偺巜摫偑扨埵悢尭偺尰忬偵偍偄偰抜乆偲婓敄偵側偭偰偒偰偄傞娭學偐傜丄崅峑尰応偱偼忚梋椶偺奣擮傪惗搆偵巜摫偡傞偺偼崲擄偵側偭偰偒偰傕偄傞丅傕偆彮偟巚峫傪楙傝丄偦偟偰傎偖偡帪娫偑梸偟偄丅侾擭娫傪捠偟偰彮偟偢偮応崌暘偗偺巚峫傪堢偰偰偄偗偽偄偄偺偱偼側偄偩傠偆偐丅
丂偲偙傠偱丄杮暥偺栤戣偺(2),(3)偼丄僼僃儖儅乕偺彫掕棟偵娭偡傞傕偺偱偁傞丅堦斒偵
|
倫傪慺悢偲偡傞偲偒丄 値p佭値丂(mod丂倫)丂丂値伕俶丂丂丂 乧乧乧(#) |
proof)
俹(値)亖値p亅値 偲偍偔丅
俹(侾)亖侽傛傝丂柧傜偐偵惉棫
俹(倣)偱惉棫偡傞偲壖掕偡傞丅丂偡側傢偪丂丂俹(倣)亖倣p亅倣佭侽丂(mod 倫)
丂丂丂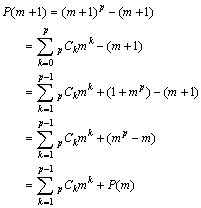
偙偙偱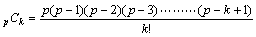
丂楢懕偡傞倠屄偺惍悢偺愊倫(倫亅侾)(倫亅俀)乧乧乧(倫亅値亄倠)偼倠両偱妱傝愗傟傞偑丄
丂丂丂倫偼慺悢丄丂侾亝倠亝倫亅侾
偱偁傞偐傜丄(倫亅侾)(倫亅俀)(倫亅俁)乧乧乧(倫亅倠亄侾)偐丣倠両偱妱傝愗傟傞丅
丂丂丂亪丂p俠k亖倫倲k丆倲k伕俶丂丂偲偍偗傞丅
丂丂丂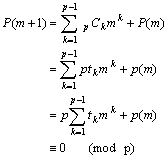
傛偭偰丂俹(倣亄侾) 偵偍偄偰傕惉棫偡傞丅
丂丂埲忋傛傝丄偡傋偰偺帺慠悢値偵偍偄偰俹(値)偼惉棫偡傞丅丂丂丂Q.E.D
丂偙偺(#)偐傜丄
丂丂丂値p亅値亖倎倫丂丂丂倎伕俶丂偲偍偔偲丄
丂丂丂値(値p-1亅侾)亖倎倫
偙偙偱(値丆倫)亖侾偱偁傟偽丄
丂丂丂値p-1亅侾佭侽 (mod 倫)
丂傛偭偰丄僼僃儖儅乕偺彫掕棟傪摼傞丅
|
n傪帺慠悢丄p傪慺悢偲偡傞丅n偲p偑屳偄偵慺偱偁傞偲偒丄 丂丂丂値p-1佭侾丂丂(mod 倫) |
丂埲忋偺徹柧偼丄忚梋宯偺奣擮傪昁偢偟傕棟夝偟偰偄側偔偰傕丄廫暘崅峑惗偑棟夝偱偒傞撪梕偱偁傞偲巚偆丅
丂嬶懱揑偵偼丄師偺傛偆側栤戣偵傕墳梡偱偒傞丅
| ex)丂丂俀1999 傪侾俋偱妱偭偨梋傝傪媮傔傛丅 |
夝)丂(俀丆侾俋)亖侾 偱偁傞偐傜丄
丂丂丂俀18佭侾丂丂(mod 侾俋)
丂丂丂俀1999亖(俀18)111丒俀
丂丂丂丂丂佭俀丂(mod 侾俋)
丂丂丂丂傛偭偰丄梋傝偼俀
丂僼僃儖儅乕偺彫掕棟偼丄俵p亖俀p亅侾側傞儊儖僙儞僰悢傊偲奼挘偟丄乽俀p-1丒俵p偼姰慡悢偱偁傞乿偲偄偆儐乕僋儕僢僪偺敪尒偵夞婣偡傞丅
丂弶摍惍悢榑偼帪娫偺棳傟偺拞傪梙傟摦偄偰偄傞偺偱偁傞丅僼僃儖儅乕偺戝掕棟偼丄崱悽婭偵偦偺徹柧偑姰寢偟偨偑丄偙偺暘栰偼傑偩傑偩嫽枴傪偦偦傞戣嵽偑杽傕傟偰偄傞丅偦偺扵媮偑崅峑惗偺抦幆偱傕壜擻偱偁傞偲偟偨傜妝偟偄偙偲偱偁傞丅偪傚偭偲偟偨嫽枴偱乽悢妛偺怟旜乿偵怗傟傞偙偲偑偱偒傞偺偱偁傞丅