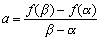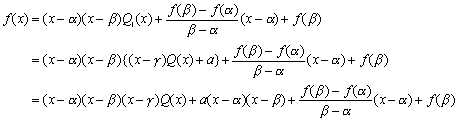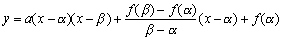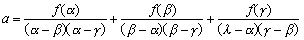<よしお> はい。直訳したP(x)=(x-α)Q(x)+Rから、余りは、
P(α)
と意訳されます。
<先 生>前時はこの翻訳(数文訳)作業まで学習したんだったね。
今日は、さらにその翻訳したものをその言語世界の中で読解することを考えてみよう。
|
ex1) 整式P(x)をx-1で割ると2余り、x-2で割ると3余る。 整式P(x)を(x-1)(x-2)で割った余りを求めよ。 |
まず、数文翻訳をしてみよう。
<かず子> 前半の条件の部分は、
P(1)=2,P(2)=3
となります。
<先 生>では、まなぶ、後半はどうなる。
<まなぶ>「えーっ、びっくり」ですね。
<かず子>なによ、それ。
<まなぶ> A=BQ+Rを早口でいうと「えーっ、びっくり」って聞こえるだろう。公式ってこうやって覚えると楽しいじゃん。
<かず子>それって、「エビ食らう」と同じくらいダサい。わーっ、いってる自分が恥ずかしい。
<まなぶ>なんだ。かず子だって語呂合わせで覚えているんじゃないか。
<先 生>まなぶ。いい加減に質問に答えてくれないだろうか。
<まなぶ>この場合は2次式で割っているから、意訳はできないので直訳して、
P(x)=(x-1)(x-2)Q(x)+R(x)
となります。で、余りは割る式より次数は低いから1次式以下より、R(x)=ax+bとおけばいいですね。
<先 生>数文翻訳したものは、
P(1)=2,P(2)=3 ⇒ P(x)=(x-1)(x-2)Q(x)+ax+b ……(*)
となるわけだ。
あとは翻訳された(*)を文章読解し、余りax+bを求めてみよう。a,bを求めるためにはxに適当な数値を代入して関係式を作ることになるけど、何を代入したらいいか、簡単に予想がつくだろう。
<よしお>xに1,2を代入するんですね。
P(1)=a+b
P(2)=2a+b
だから、
a+b=2,2a+b=3
これを解いて、a=1,b=1
よって、余りはx+1となります。
<先 生>この問題の面白いところは、整式P(x)が具体的な形で示されていないことだ。それなのに余りだけは確定してしまうという妙な問題だ。これを和文だけで解釈しようとすると余計分かりにくくなってしまうけど、このように数文に翻訳してみるとずいぶんすっきりする。数学の問題は、数学の世界でその思考を含めて考えた方がラクということだね。では次の問題。
|
ex2) P(x)をx-1で割った余りが3,(x-2)(x-3)で割った余りが3x-2であるとき、 整式P(x)を(x-1)(x-2)(x-3)で割った余りを求めよ。 |
まなぶ、条件の部分を数文訳してごらん。
<まなぶ>簡単です。まず前半の条件は意訳するから
P(1)=2 ………①
後半は2次式で割るので意訳はできないから「えーっびっくり」で直訳して、
P(x)=(x-2)(x-3)Q(x)+3x+2 ………②
となります。
<先 生>オーケー。割る式が1次式の場合は意訳ができるけど、2次式以上の場合は直訳しかできないことに注意しよう。では求める余りを数文訳してみよう。
<よしお>3次式で割るので、余りは2次式以下だから直訳して、
P(x)=(x-1)(x-2)(x-3)+ax2+bx+c ……③
となります。
<まなぶ>バトンタッチ。僕が解いて進ぜよう。
③にx=1,2,3を代入して、
P(1)=a+b+c
P(2)=4a+2b+c
P(3)=9a+3b+c
条件②から、P(2)=4,P(3)=7だから、
a+b+c=3
4a+2b+c=4
9a+3b+c=7
これを解いて、えーっと、……… a=1,b=-2,c=4
だから、余りはx2-2x+4です。
<先 生>何かまなぶひとりで片付けてしまったな。まっ、それだけ簡単ということだ。
<まなぶ>どういう意味でしょ。
<先 生>おほん!。では最後の問題だ。
|
ex3) 整式P(x)をx-2で割った余りが3、(x-1)2で割った余りが2x+1であるとき、 整式P(x)を(x-2)(x-1)2で割った余りを求めよ。 |
<かず子>前の問題と同じね。まなぶにもできるんだから今度は私が解きます。
まず、条件の最初の方は意訳して、
P(2)=3 ……①
次の条件は2次式で割ってるから直訳して、
P(x)=(x-1)2Q1(x)+2x+1 ……②
となるわ。3次式で割るから求める余りは2次式以下より、
P(x)=(x-2)(x-1)2Q(x)+ax2+bx+C ……(*)
あとは、xに値を代入してa,b,cを求めればいいわ。
で、代入する値はもちろんx=1とx=2と、………、あれっ、変だわ。
<よしお>僕もそう思う。a,b,c3つの変数の値を求めるわけだから、代入するxの値が足りないね。
<まなぶ>なんだ、かず子。人のことをとやかく言えないよな。
<かず子>うるさいわね。先生、これ問題ミスじゃないんですか。
<先 生>ミスじゃないよ。
<よしお>でも先生、条件②で代入できる値は、x=1しかないわけですから、意訳すると
P(1)=3
しかでませんよね。やっぱり一つ条件が足りないような気がしますが。
<先 生>では逆にP(1)=3を和文訳したらどうなる。
<かず子>「P(x)をx-1で割ると余り3」ということですね。あれ、②の意味にならないわ。
<先 生>その通り。つまり②の条件を部分的にしか使ってないから条件が足りないように感じてしまうんだ。②を(*)に式に最大限に反映させることを考えてみよう。(*)の右辺をよくみてごらん。
<生徒達> ………
<まなぶ>先生、(*)の右辺はP(x)を(x-1)2で割った式のようにも見えますよね。そのときの商が(x-2)Q(x)で余りがax2+bx+cと考えられないでしょうか。
<かず子>何いってんのよ。2次式(x-1)2で割ってしまったら、余りは1次以下でしょ。「えーっ、びっくり」なんてこじつけで覚えているから商と余りの大事な関係を見落とすのよ。
<まなぶ>心外だなあ。ちゃんと考えてるよ。a=0とすると1次以下になるじゃないか。
<よしお>うーん。そう都合よくいけばいいけど、(*)の式はもともとは3次式で割った余りを表しているわけだから、a=0としてしまうと、常に余りが1次以下になってしまうよ。
<まなぶ>なるほどな。よしおの説明ならよく分かるな。残念。いいアイデアだと思ったんだけどなあ。
<先 生>先生は、いいアイデアだと思うよ。だって、(*)の余りを1次以下にすればいいだけの問題だろ。
例えば、30を7で割った余りを
30=7×3+9
として、余り9とするわけにはいかないだろ。この式から本当の余りを求めるにはどうする。
<かず子>9をさらに7で割って、
9=7×1+2
から2が余りです。そうか。同じことを(*)でもやればいいんだわ。
<よしお> ax2+bx+cを(x-1)2で割るってことですね。それじゃ実際に割ってみると……、
ax2+bx+c=a(x-1)2+(2a+b)x+(c-a)
これが②の余り2x+1に一致すればいいということですね。だから、
2a+b=2,c-a=1
やった。2つ分の式がでてきました。
これと、P(2)=3から、4a+2b+c=3
3つの式から を求めて、a=-2,b=6,c=-1
よって余りは-2x2+6x-1となります。
ふーっ、やっとできました。結構面倒ですね。
<先 生>そうだね。今のような解き方をすると確かにそうかもしれない。
<かず子>あれ?、違うんですか。
<先 生>いまのやり方は(*)の余りを②の余りに一致するように変形したということだね。でもまなぶのいっていたことはP(x)を(x-1)2で割ったとき、商は(x-2)Q(x)に見えるということだ。そう考えるとそれは②の商Q1(x)に一致するってことになるね。
<かず子>なんで先生まで、まなぶの与太話に付き合ってるの。一致するなら、
Q1(x)=(x-2)Q(x)
と変形できるってことですよね。そんなに上手くいくわけないわ。
<先 生>確かにそうだ。そんな都合よくいかない。ところで、かず子の言ってた式を和文訳するとどうなる。
<かず子>整式Q1(x)をx-2で割ったら商がQ(x)で割り切れるということです。でも絶対、割り切れるはずないわ。
<先 生>ということは、余りがでるということだよね。
<よしお>うーん、僕も先生の意図していることが何なのかよく分からないのですが……。でも、仮に無理に一致させるなら、1次式で割るから余りは定数になるわけですから、余りを とすると、
Q1(x)=(x-2)Q(x)+a
が正しい関係式ということになりますね。
<先 生>その通り。ではそれをためしにちょっと②に代入してごらん。
<よしお>はい、代入して整理すると、
P(x)=(x-1)2{(x-2)Q(x)+a}+2x+1
=(x-1)2(x-2)Q(x)+a(x-1)2+2x+1
あれっ?、このa(x-1)2+2x+1の部分ってまさか……。
<まなぶ>余りだ!
<先 生>気がついたみたいだね。この部分の次数を考えると2次以下の式であることは明らかだろう。すると割る式と余りの次数の関係から整式P(x)を(x-1)2(x-2)で割ったときの商はQ(x)で余りがa(x-1)2+2x+1ということにならざるを得ない。
<かず子>分かった。そうすると、あとはaを求めるために、P(2)=3を利用すればいいんですね。
P(2)=a+5=3より、a=-2
だから余りは、
-2(x-1)2+2x+1=-2x2+6x-1
となります。確かにこの方法だと求める変数が だけだからずいぶん簡単にできるわ。
<まなぶ>どうだい。僕の直感は大したものだろう。ところで先生。いまの解法は他の問題にも応用できないんですか。
<かず子>また、まなぶの本能だけの動物的直感なの。
<まなぶ>直感じゃないよ。だってね。かず子がいっていたように、ex2の問題も同じような条件設定になっているだろう。P(x)を(x-2)(x-3)で割った余りが3x-2なら、
P(x)=(x-2)(x-3)Q(x)+3x-2
から、Q1(x)をx-1で割った商をQ(x)、余りをaとすると、
Q1(x)=(x-1)Q(x)+a
と表されるから、
P(x)=(x-2)(x-3){(x-1)Q(x)+a}+3x-2
=(x-1)(x-2)(x-3)Q(x)+a(x-2)(x-3)+3x-2
あとは、P(1)=3から
P(1)=2a+1=3 ∴ a=1
と求められるから余りは
(x-2)(x-3)+3x-2=x2-2x+4
ほら、できた。
<かず子>すごい、まなぷ。ちょっと見直しちゃった。ということは先生。ひょっとしたらex1)も同じようにできるのではないでしょうか。
<まなぶ>かず子、やってみろよ。
<かず子>まず、P(x)をx-1で割った余りが2だから、これを意訳でなく直訳すると、
P(x)=(x-1)Q1(x)+2
ここで、Q1(x)をx-2で割った商をQ(x)、余りをaとすると、
P(x)=(x-1){(x-2)Q(x)+a}+2
=(x-1)(x-2)Q(x)+a(x-1)+2
あとはP(2)=3なんだから、
P(2)=a+2=3 ∴ a=1
だから余りはx+1となるわ。
<まなぶ>やるじゃん、かず子。
<先 生>だいぶ諸君も数学の世界での思考法に慣れてきたみたいだね。日本語は感情言語の代表的なものだから、和文で数学を語ろうとするとどうしても曖昧な部分がでてくる。それに比べて論理言語である数学語は単純極まりない。だから問題解法も数文で読解した方が当然組し易いわけだ。通訳する人たちだってそうだろ。彼らは相手の言語で考え、日本語で考え、それぞれの言葉に翻訳するはずだ。数学も同様に翻訳の達人すなわちバイリンガルになれば感情がないだけ実にシンプルにお互いを語り合えると思うよ。
<かず子>わたしとまなぶも数学の世界の中では多少は友達付き合いできるかもしれないわね。