

○遠回りしましょ!
<先 生>
|
ex) 次の数列{an}の一般項を求めよ。 (1) 1・1, 2・3, 3・5, 4・7, 5・9, 6・11………… (2) 1,1+2,1+2+4,1+2+4+8,1+2+4+8+16,1+2+4+8+16+32………… |
よしお、解答してごらん。
<よしお>
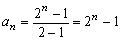
<先 生>
|
ex) 次の数列{an}の一般項を求めよ。 (1) 1, 6, 15, 28, 45, 66, ………… (2) 1, 3, 7, 15, 31, 63, ……………… |
<先 生>
<生徒達>
<かず子>
<まなぶ>
<よしお>
<まなぶ>
<かず子>
<先 生>
<まなぶ>
<先 生>
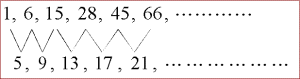
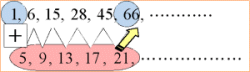
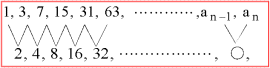
どうだろう。隠されていた数列の規則性を暗示するような項の並びが現れてこないだろうか。これも、ひとつの数列と考えることができる。この数列を元の数列の階差数列という。ところでこの階差数列はどんな規則性をもっているだろうか。
<まなぶ>
<先 生>
<よしお>
<先 生>
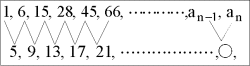 これから第n項anを分解すると
これから第n項anを分解すると<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<よしお>
<先 生>
<かず子>
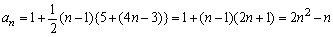
<先 生>
<かずお>
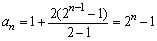
<先 生>
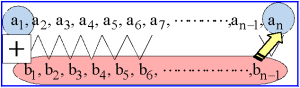 数列{an}の階差数列を{bn}とする。
数列{an}の階差数列を{bn}とする。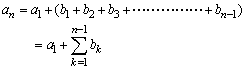
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<かずお>
<先 生>
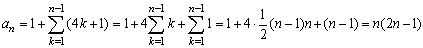
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<生徒達>
<よしお>
<先 生>
<よしお>
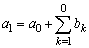
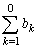 は、初項から第0項までの和となって意味をもたないからです。
は、初項から第0項までの和となって意味をもたないからです。
<先 生>
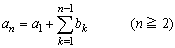
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
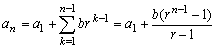
<かず子>
<先 生>
<よしお>
<先 生>
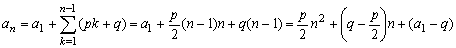
|
ex) 次の数列{an}の一般項を求めよ。 2, 4, 9, 17, 28, 42, 59,………… |
<まなぶ>
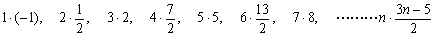
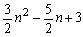
<先 生>
あとがき
数列の多くの問題は、「一般項とその和を求めよ」という問題に帰着してしまいます。では、どうやって求めるかということの方法論の展開と考えて差し支えないでしょう。その中で階差数列の位置付けはというと、端的にいうと「回り道の論法」ということになるかもしれません。しかし実際は、規則性の見出せない数列の項を羅列して、どうすると迫ってしまう。そうではなくて、「一般項が見つかればいいんだけれど見つからない場合は回り道をすることで求められる」というように非常手段として押さえることで教わる側も安心するのではないでしょうか。
本文の後半は、まったくの脚色で、ナンセンスな内容になってしまいました。こういった考え方をすると何でもありになってしまいます。nの2次式になるのなら、3点 (1,a1),(2,a2),(3,a3)を通る放物線の方程式を求めてもいいということでしょう。
ただ、階差数列による解法の2つの2つの点は、やはり頭を悩ますことではあります。
① 階差数列の初項からn-1項までの和の計算
② n≧2の制限
これを何ととか解消する手立てということで本文の後半を書いたのですが失敗でした。n-1の問題は、
Sn= an-an-1
でも扱うわけですから、もちろん指導上大事なこととは思いますが、階差数列の場合はやっぱり付けたしという感は否めません。
そこで、ちょっと別の観点からこのことについて考えてみましょう。
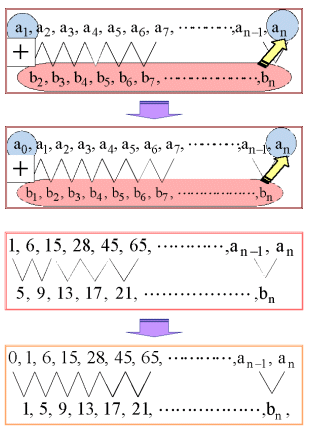 ①,②という2つの問題点を上で列挙しましたが、実はこの2つは本質的には同じものです。①の計算のために②を考える必要が生じたと解釈した方がいいかもしれません。それならば、階差数列の和をn項目までとるようにすれば問題は解決するということになります。そこで、
①,②という2つの問題点を上で列挙しましたが、実はこの2つは本質的には同じものです。①の計算のために②を考える必要が生じたと解釈した方がいいかもしれません。それならば、階差数列の和をn項目までとるようにすれば問題は解決するということになります。そこで、
bn=an-an-1 (n≧2)
ように一つ階差をずらしてやります。すると、
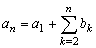
となります。しかしこの場合もn≧2でしかanは求められません。それで、ここでダミーとしてあらかじめa0を定義しておけば、
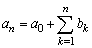
となりすべての自然数nに対してanは求められることになります。
本文の例題で考えてみましょう。ex)(1)は、右図のように階差が4の等差数列ですから階差数列の初項として、
b1=5-4=1
を考え、さらにa0=a1-b1 とすれば、
a0=1-1=0
となります。以上より、次のように解答します。
a0=0 とすると、階差数列{bn}の一般項は、
bn=4n-3
よって、
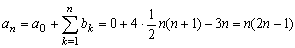
となります。同様に、ex(2)についても、
a0=0 (b1=1 に対して)
と定義すると、bn=2n-1ですから、
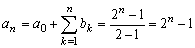
さらに、漸化式についても次のように扱えばいいことになります。
|
ex) 次の漸化式で与えられる数列{an}の一般項を求めよ。 a1=3, an+1-an=3n+1 |
n=0を代入して、a1-a0=1 ∴ a0=2
{an} (n≧0) の階差数列は、
bn=an-an-1=3n-2
より、
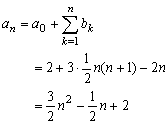
さて、この解法は市民権を得るでしょうか。