札幌新川高等学校　中村文則

○彼方の世界へ

ex) 3100は何桁の数か求めよ。ただし、log10x=0.4771 とする。

＜先　生＞まず、x=3¹⁰⁰とおいて、両辺の常用対数をとります。
　　　log₁₀x=log₁₀3¹⁰⁰=100log₁₀3=47.71
　ここで、大雑把に考えれば、
　　　47＜log₁₀x＜48
ということになるね。ところで、47=47log₁₀10=log₁₀10⁴⁷ 。48についても同様に考えると、
　　　log₁₀10⁴⁷＜log₁₀x＜log₁₀10⁴⁸
　対数関数 log₁₀x は増加関数だから、真数を比較すると、
　　　10⁴⁷＜x＜10⁴⁸
　この式からxの桁数を求めることができる。まなぶ、何桁だろう。

＜まなぶ＞うーん。ちょっと値がでかすぎて……。

＜先　生＞そういうときはもう少し分かりやすい桁数に引き降ろしてやればいい。
　　　10²＜x＜10³
だとどうだい。

＜まなぶ＞それなら分かります。xは100から999までの整数だから、3桁です。

＜先　生＞そうだね。ではその3桁の3ともとの不等式との関係を考えてごらん。

＜まなぶ＞そうか。右辺の指数の値に一致しているから……、分かりました。48桁です。

＜先　生＞そうだね。このように常用対数を利用すれば大きな数の桁数を求めることが可能になるんだ。でもね。よく考えるとこの桁数っていうのはずいぶん乱暴な数字ではないだろうか。

＜よしお＞どうしてですか。

＜まなぶ＞ぼくは分かるな。先ほどの3桁の例で考えればいいんだ。3桁の数のお金を貰えるとしたとき、100円を貰うのと、999円を貰うのではぜんぜん違うよ。

＜かず子＞なるほど。それに対して999円と1000円じゃ、3桁と4桁なのにほとんど同じように感じるわね。

＜先　生＞うん、だから桁数を求めただけでは、例えば恒星の距離なんかを調べる場合なんかは不正確な値だということがわかるだろう。桁数だけでなく、ある程度の大きさを示す値、すなわち最高位の数が何なのかということも大事なことになってくる。

＜かず子＞でも、先生、最高位の数は求めることができるんですか。

＜先　生＞そのヒントは先ほどの解答の中にあるんだ。さて、どこだろう。

＜よしお＞分かりますよ。先生が「大雑把に考える」といったところですよね。

＜先　生＞そのとおり。先ほどは、
　　　log₁₀x=47.71　　……(*)
からその小数部分を無視してずいぶん大雑把に範囲を考えてしまったね。実はこの小数部分が最高位の数を決定しているんだ。上の(*)の式の意味をもう一度考えてみよう。
　(*)を指数の形で表現すれば、
　　　x=10^47.71=10^0.71･10⁴⁷
ここで、
　　　1=10⁰＜10^0.71＜10¹＜10
　これから、10⁴⁷ が桁数を表し、10^0.71 が1桁の数を表していることになる。だから10^0.71 のおおよその値が分かれば、その整数部分が求める最高位の数というわけだ。

＜まなぶ＞でもどうやってそれを求めればいいんですか。

＜先　生＞それは、問題文で与えられていた log₁₀3=0.4771 から予想がつくだろう。対数の意味を考えれば、これは何をいってるんだろう。

＜よしお＞そうか。対数から指数の変換を考えれば、
　　　10^0.4771=3
ということですね。これから 3=10^0.4771＜10^0.71 だから、10^0.71 は3より大きい値だということが分かりますよね。これと同じように、1桁の整数が10を底として表現できればいいのではないでしょうか。

＜先　生＞その通り。対数は、数を底を統一して表現するための潤滑油のような働きをするんだ。なお、底を10にするにはもうひとつ必要な対数の値がある。
　　　log¹⁰2=0.3010
　この値を使って1から9までの整数を底を10として表してみよう。例えば、
　　　log₁₀4=2log₁₀2=0.6020
というようにだ。他の数はどうなるだろうか。

＜まなぶ＞ log₁₀8=3log₁₀2=0.9030、log₁₀9=2log₁₀3=0.9542 さらに
　　　log₁₀6=log₁₀2+log₁₀3=0.7781
となります。で、log₁₀5 はというと……。どうすればいいんだろう。

＜よしお＞ log₁₀5=log₁₀10/2=log₁₀10-log₁₀2=0.6990 とすればできるよ。あとは、7だけどこれはできるんだろうか。

＜先　生＞実は7は求められないんだ。2や3と同じようにふつう、近似値 log₁₀7=0.8451 で与えられている。さあこれで次の対応表が完成したことになる。

　この表から、10^0.71 のおおよその値を読み取ってみよう。

＜よしお＞ 5=10^0.6990＜10^0.71＜10^0.7881=6 ですから、5.○○○の数です。したがって、最高位の数は５ということになります。

＜かず子＞凄い。求まっちゃうんだ。これでかなり正確な値が分かったことになりますね。

＜まなぶ＞でもね、先生。3桁ぐらいの数なら500円と599円はそんなに気にならないけど、50,000円と59,999円だったらずいぶん違うと思うな。ましてや48桁になると凄い差がでてくるわけで、最高位の次の数も必要なのではないでしょうか。

＜先　生＞まなぶはどうしてもお金と結びつけたいようだね。でもいっていることも一理ある。では、どうやったらその数は求められるだろうか。

＜よしお＞ 1＜10^0.71＜10 だから、10＜10^1.71<100 です。ですから 10^1.71 が2桁の整数で表現できればいいわけですけどそんなの無理ですよね。

＜かず子＞私も無理だと思うわ。2桁の数すべてが10を底として表現できなければいけないってことでしょ。

＜先　生＞そうだね。確かに難しそうだね。でもこの場合は数の範囲は50〜60の間に限定されているから可能性はある。できるかどうかは分からないけれどtryだけはしてみようか。ただ、10⁴⁷の部分は桁数を表していたわけだから、2桁の数として考えると、桁数も調整しなければいけないことになる。だから桁数をいじるのではなく、10^0.71 の小数第1位の数はなにかと考えた方がいいだろう。
　まずは、大雑把に予想してみよう。5の次の数字はみんなは何だと思う。

＜よしお＞先ほどの換算表をみると10^0.71は5の方に近い値だから、5.2、5.3 くらいの値じゃないでしょうか。でもこの2つの値の対数を計算することはできないと思います。

＜かず子＞でも 5.4 はできるわ。5.4=2･3³/10 でしょ。

＜先　生＞やってみよう。
　　　log₁₀5.4=log₁₀2+3log₁₀3-log₁₀10=0.7323＞0.71
　狭まってきたね。これから、5.0，5.1，5.2，5.3 のいずれかの値ということが分かるね。では、また予想だ。この中のどの値だろうか。

＜まなぶ＞僕は、5.1台だと思うな。 log₁₀5=0.6990、log₁₀5.4=0.7323 なんだから、0.71 との開きを考えると、
　　　0.71-0.6990=0.011　　　0.7323-0.71=0.0223
　この開きの差をみると、5と5.4の中点である5.2より値は小さくなきゃいけないだろ。

＜よしお＞僕も5.1台だと思います。ただ、底が10のときの対数関数のグラフの曲線の曲がり方をみると、5と5.4の中点を基準にするわけにはいかないと思う。中点の5.2よりだいぶ左にずれて、値は5.1の方に近づくんではないでしょうか。

＜先　生＞だいぶ煮詰まってきたね。みんなの結論は5.1台の数ということだけど、さあそれをどう確認したらいいだろうか。

＜まなぶ＞小数第1位で調べにくいのなら小数第2位の値まで広げて考えてみたらどうでしょうか。

＜かず子＞5.10〜5.20の間ということね。5.10，5.11，5.12，……、あっ、512って確か、2のべき乗の値よね。

＜よしお＞9乗だよ。そうか、この値で判定できるね。
　　　log₁₀5.12=log₁₀2⁹-log₁₀10²=0.709

＜まなぶ＞やったね。もうほとんど0.71といっていい値だ。

＜先　生＞確かに5.1台の値ということは間違いがないと思うけど、やっぱりここは厳密に判定しなきゃいけない。確認しよう。現時点で分かっていることは、
　　　5.12=10^0.709＜10^0.71＜10^0.7323=5.4
ということだ。したがってもう一つ近似できる5.1台の値を見つければいいんだ。

＜まなぶ＞2と3のべき乗を考えてもそんなの見つからないないなあ。先生やっぱり無理ですよ。大雑把に5.1台でいいんじゃないですか。

＜かず子＞なにいってんの。まなぶが最初に求められないかって聞いたんでしょ。勝手なんだから。

＜よしお＞まてよ、先生、平方数で考えるっていうのはどうでしょう。

＜先　生＞どういうことだろう。

＜よしお＞5.12⁶=26.01ですから26近辺の数を考えて平方根をとるんです。27なんかがいいのではないでしょうか。

＜まなぶ＞いっていることがよくわからないよ。

＜よしお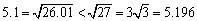＞ ですよね。ここで、
　　　
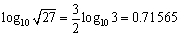
　これから、10^0.71565=5.196

＜まなぶ＞やった！。見つかったじゃん。
　　　5.12=10^0.709＜10_0.71＜10^0.71565=5.196
　やっぱり、5.1台の値だ。最後まで諦めないでよかった。

＜かず子＞ほんと勝手なんだから。図に乗って小数第2位は何かなんて聞かないでよ。

＜まなぶ＞僕はそこまでしつこいないよ。

＜先　生＞もうこれだけ求めれば十分だろう。かず子が最初にいっていたように、基本的にはすべての数が2と3を底とする指数の積として近似できなければ求められない数もでてくる。小数第2位となるとずいぶんそれは難しいのではないだろうか。
　でもね、実は3¹⁰⁰の1の位の数は簡単に見つけられるんだよ。3の累乗を順次計算すると、
　　　3¹=3，3²=9，3³=27，3⁴=81，3⁵=243
だね。このそれぞれの1の位の数だけ追いつづければどうなるだろう。

＜よしお＞次の3⁶の1の位は9で、その次は7ですよね。先生、分かりました。サイクリックに繰り返しているんですね。

＜まなぶ＞ なるほど、3，9，7，1の繰り返しってことか。だから3¹⁰⁰がこの繰り返しの何番目にあるか分かればいいんだ。

＜かず子＞ 3¹⁰⁰=(3⁴)²⁵とかんがえれば、25回繰り返しているわ。だから、1の位の数は1ですね。

＜まなぶ＞先生、同じように考えると、十の位の数も求められますよね。

＜よしお＞えっ、まなぶ、どうやるの。

＜まなぶ＞2桁の数でサイクリックに繰り返す範囲を求めればいいんだろ。(鞄から電卓を取り出して……)えーっと、べき乗を計算すると、
　　　3，9，27，81，243，729，2187，6561，……
　あれっ、なかなかでてこないなあ。(ひたすら電卓を叩いて)
　　　………，3²⁰=3486784401，
　あっ、やった、みつけた。20乗して、下2桁が01なんだから、
　　　3¹⁰⁰=(3²⁰)⁵=(………01)⁵=…………01
　だから、十の位の数は0だ。

＜よしお＞凄いね。でも、電卓を使うのは反則だと思うな。

＜かず子＞それにしても、しつこいわねえ。やっぱりまなぶはまなぶなのね。

＜先　生＞まなぶの100乗はまなぶということかな。

＜まなぶ＞先生、ひどいや。

あとがき

　　　「最高位の数は何か」、「小数第何位に初めて０以外のどんな数が現われるか」

といった探求にあり、1の位の数が底を10とする指数で表現できることに醍醐味があります。
　しかし、残念なことに、素数7に関しては例外として扱われるために、指導の際もちょっとテンションが下がってしまうものです。
　したがい、7の表現が可能ならこれはかなりのインパクトがあるといえるでしょう。それを本文では、「無理」と簡単に片付けてしまっていますが、実は可能なのです。
　例えば、本文にあるように「平方して数を判定する」という方法で考えてみましょう。7²=49とみると、
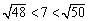　ですから、
　　　
　　　
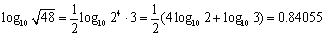
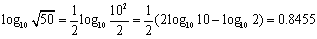
　これから、 0.84055＜og₁₀7＜0.8455　となります。この程度の近似で十分かと思いますが、実はもっと簡単に近似することも可能です。
　7⁴=2401 から、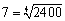 とするのです。計算すると、 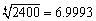ですからほぼ7とみなしていいわけです。これより、
　　　
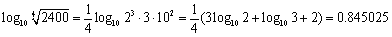
　実際の7の対数は、log₁₀7=0.8451 ですからかなりイイ値だということが分かるでしょう。ちなみにこの値は「はよ来い」なんで覚えればいいのでしょうか。ところで、3の対数は「死なない」と語呂合わせするのは有名ですが、2の対数はどう命名すればいいのでしょうか。「サオ入れ」とか「サボテン」とかどれもちょっと無理があるような。
　なお、この7⁴の値から、後半の3¹⁰⁰の十の位の値を求めることが可能になります。
　　　
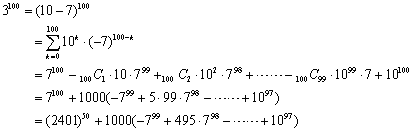
　これから十の位の数字が0であることが分かります。また、
　　　2401⁵=79792266297612001
であることより、3¹⁰⁰の百の位の数も0となります。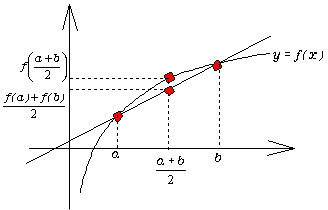
　次に、本文中、まなぶが、5.0と5.4の平均から の小数第1位を予想することに対して、よしおが対数関数のグラフから5.1の値により近づくと述べていますが、一般に上に凸な関数については次の性質が成立します。
　　　
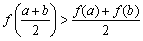
　このことを利用すれば、a=5.0，b=5.4，f(x)=log₁₀xとみると、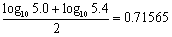から、
　　　0.71＜0.71565＜log₁₀5.2
　これから、10^0.71≒5.1 が得られます。
　この考えも、近似値を求めるには有用な方法といえるでしょう。
　さて、ところで本文中では、任意の数を2と3を底とする指数を使って表現することは難しいといっていますが、では実際にはどこまで可能なのでしょうか。
　下表は、2^m･3ⁿ (1≦m,n≦10) の値を示したものです。その値を近似的にみることで、素数の近似値を求めることができます。
　例えば、2⁵･3⁷=69984≒70000 とみて、両辺に常用対数をとると、
　　　log₁₀7=5log₁₀2+7log₁₀3-4=0.8447
　同様に
　　　
　　　
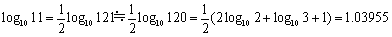
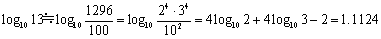
といった具合です。実際の近似値 からみてもまあまあの値です。
　さらに、対数の値が与えられていなくとも、近似的に値を算出できます。例えば、log₁₀2¹⁰=1024≒10³ から、log₁₀2=0.3333 となります。もう少し正確な値を求めるなら、x=log₁₀2，y=log₁₀3 とおくと、
　　　2²･3⁵=972≒10³ から、　　2x+5y=3 ……�@
　　　2⁹･3⁹=10077696≒10⁷ から、　　9x+9y=7　　　……�A
　これを解いて、x=8/27=0.296，y=13/27=0.481 となります。
　さらに、z=log₁₀7 とすると、
　　　2⁵･3⁷=69984≒7･104 より、5x+7y=z+4　　　……�B
　　　2¹⁰=1024≒10293･7³ より、10x=y+3z　　　……�C
�A，�B，�Cを解くと、
　　　x=46/153=0.3007，y=73/153=0.4771，z=129/153
　ほぼ、対数表の近似値に一致します。
　ちなみに、�Bの式は、下表の2と3のべき乗の対応のいたるところで顔をのぞかせます。

【２と３のべき乗表】

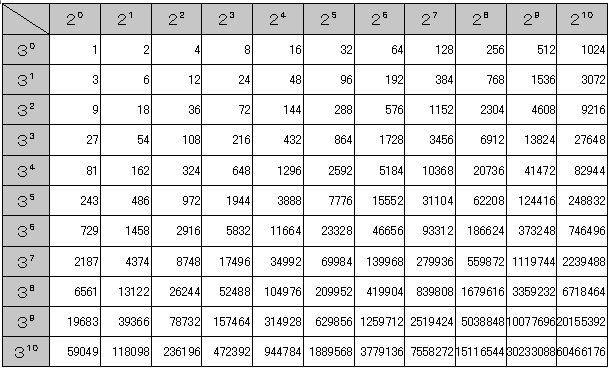
　では次に、整数以外の数のべき乗の桁数について求めてみましょう。円周率πの100乗を例にとります。
　超越数である円周率はよく無理数 で近似されますが，この値では100乗すると 10⁵⁰ でありかなりの誤差がでてきます。もう少し、正確な値を求めて見ましょう。
　まず、π＜3.15ですから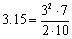， より，
　　　log₁₀π＜2log₁₀3+log₁₀7-log₁₀2-1=0.9483
　次に，π²＞3.14²=9.8596＞9.8=2･7²/10 から，
　　　log₁₀π＞(log₁₀2+2log₁₀7-1)/2=0.4956
　故に
　　　10^49.56＜π¹⁰⁰＜10^49.83
　よって、π¹⁰⁰は50桁の数になります。
　なお、上述の2と3のべき乗表をみると、2⁴･3⁹=314928≒π×10⁵ ですから，
　　　log₁₀π≒4log₁₀2+9log₁₀3-5=0.4979
と近似できます。実際、関数電卓で計算すると、log₁₀π≒0.4971 ですから、イイ値です。
　と、まあ、以上、数字をいじくってみましたが、ここまで凝るのは「まなぶ的やりすぎ」兆候かもしれません。
　だいたい、本文中の【1桁の整数のべき乗換算表】をみても、4桁の対数表と比較すると、その数値にはズレがあります。これは4桁の対数表そのものが近似値だからです。例えば、log₁₀2=0.3010 として、2⁹⁹⁹⁶ を計算すると 2⁹⁹⁹⁶=10^3008.8 より、3009桁となりますが、実際の値は、2⁹⁹⁹⁶=10^3009.1 であり、3010桁となります。小数第4位以下の部分のズレは、対数を足し引きしているとだんだん大きくなってくるのです。100乗のような天文学的な数は、もうこの世の実在を超越しているわけで、多少どころか大幅にズレていようとどうってことないのかもしれません。
　漸化式の好例として出題される、かの有名なハノイの塔の問題では、バラモン僧が64枚の円盤を移し替えるのに要する手数である2⁶⁴-1でこの世は終焉を迎えるとしています。1手の移動を1秒と考え，完成までの総日数を計算すると，およそ5931億日となります。
　べき乗表をみると，3¹⁰=59049ですから，
　　　5931億日≒3¹⁰×10⁸=1047.71×10³=10^50.71
　これはπ¹⁰⁰=10^49.71 をほんのちょっと？超えた値です。こんなもので現世は空蝉となります。ましてや人生のちっぽけなこと。
　ちょっと計算してみましょう。
　人間の寿命を80年位とし，既に無駄に30年を費やしたとします。残り50年のうち，1日8時間は寝ているとして、活動し生活している時間を全体の と考えます。1年を365日として，活動時間の総秒数を計算すると、
　　　50×2.3×365×24×60=1051200000≒10⁹
　10億秒、これが人生です。こんな計算をくどくどとやっているだけでも300秒ぐらいは使っているでしょうか。
　ということで、だんだん馬鹿らしくなってきたのでこの辺でこの話はやめましょう。
　最後に、まなぶがべき乗の大きさをお金で実感する場面が本文にありますがそのことについて一言。
　対数はいろいろな分野で応用されますが、ひとつに心理学において、フェヒナーの法則というのがあります。
　感覚の強さEは、刺激の強さRの対数に比例するというもので、関係式
　　　E=k logR
で表されます。これは、ある意味では人間の刺激への順応性と解釈することができます。過度の刺激に対する麻痺がなければ人間は発狂してしまうかもしれません。しかし、こと金が絡むとそうではないことをまなぶは指摘しています。
　例えば消費税については、それを支払いことは国民の義務であると同時に痛みでもあります。この痛みという感覚、金額が大きくなればなるほど増大します。20万円のコンピュータの消費税は1万円です。これはもうショックです。この場合の感覚は，
　　　e=k e^R
とでもなるのでしょうか。
　どうやら，3¹⁰⁰というどうでもいいくらい大きな数字でも、金銭の欲や、数学の探求欲に関しては人間、際限はないようです。