

|
ex) 師偺晄摍幃傪悢妛揑婣擺朄傪棙梡偟偰徹柧偣傛丅 (1) 俀n+2亄俁2n+1偼俈偺攞悢偱偁傞丅 (2) 俀n亜俀値亅侾 |
亙愭丂惗亜偲偙傠偱悢妛揑婣擺朄偭偰偳傫側徹柧朄偩偭偨傠偆偐丅
亙傑側傇亜帺慠悢偵娭偡傞柦戣傪徹柧偡傞応崌偵丄僪儈僲搢偟偺曽朄傪棙梡偟偰丄弴斣偵彫偝偄帺慠悢偐傜惉棫傪搢偟偰偄偔傫偱偟偨傛偹丅
亙愭丂惗亜惉棫傪搢偡偭偰偄偄偐偨偼柺敀偄偹丅傕偆彮偟嬶懱揑偵偄偆偲偳偆側傞偺偩傠偆丅
亙傛偟偍亜傑偢丄戞倠斣栚偑惉棫偡傞偲壖掕偟傑偡丅師偵丄偦傟傪棙梡偟偰倠亄侾斣栚偱惉棫偡傞偙偲傪徹柧偟傑偡丅
亙愭丂惗亜偦偆偩偹丅柦戣偑摍幃傗晄摍幃偱偁傟偽丄壖掕偟偨倠斣栚傪忦審幃偲偟偨応崌偵丄倠亄侾斣栚偺幃傪徹柧偲偄偆偙偲偩丅偦偟偰乧乧
亙傑側傇亜嵟屻偵侾斣栚傪搢偡傫偱偡偹丅偦偆偡傞偲丄侾斣栚丄俀斣栚丄俁斣栚丄乧乧偲師乆偵搢傟偰偄偭偰丄僊僱僗僽僢僋偵嵹傞丅
亙偐偢巕亜偦傟丄壗偺偙偲丅
亙傑側傇亜僥儗價偺摿斣偱丄偲偒偳偒傗偭偰傞偩傠偆丅慡崙偐傜廤傑偭偨崅峑惗偑崌廻偟偰僪儈僲傪嬯楯偟偰暲傋偰僊僱僗偵挧愴偡傞偭偰斣慻丅
亙愭丂惗亜挷巕偵忔傝夁偓偩側丅偱傕丄嬯楯偟偰暲傋傞偭偰偲偙傠偼徹柧偺杮幙傪偄偭偰偄傞丅婣擺朄偼乽壖掕偟偨傕偺傪棙梡偟偰徹柧傪偡傞乿傢偗偱丄僪儈僲搢偟傕幚嵺偵搢偟偰偟傑偭偨傜戝僸儞僔儏僋偩偹丅嵟屻偵扤偐偑侾斣栚偺僪儈僲傪恖嵎偟巜偱偪傚偙偭偲墴偟偰搢偡偙偲偱丄僪儈僲偑師乆偵搢傟偰偄偔條傪挱傔傞偙偲偵帄嬌偺婌傃偑偁傞丅
亙傑側傇亜愭惗傕偪傚偭偲丄挷巕偵忔傝夁偓偰側偄丅
亙愭丂惗亜偍傎傫両丄偠傖丄偦傠偦傠栤戣傪夝偄偰偄偙偆丅傑偢(1)偩丅傛偟偍丄偳偆偡傞丅
亙傛偟偍亜傑偢丄値亖倠偱惉棫偡傞偲壖掕偟傑偡丅
丂丂丂乽俀k+2亄俁2k+1偼俈偺攞悢偱偁傞乿
丂偙傟傪忦審偲偟偰丄値亖倠亄侾偱惉棫偡傞偙偲傪徹柧偟傑偡丅偡側傢偪丄
丂丂丂乽俀(k+1)+2亄俁2(k+1)+1偼俈偺攞悢偱偁傞乿
偙偲偺徹柧偱偡偹丅
亙愭丂惗亜偱偼丄徹柧偟偰偛傜傫丅
亙傛偟偍亜乧乧乧丄嵪傒傑偣傫丄愭惗丅偳偆徹柧偡傟偽偄偄偐僸儞僩傪偄偨偩偗傑偣傫偐丅
亙愭丂惗亜傛偟偍偵偟偰偼捒偟偄偹丅側偵傕擄偟偔峫偊傞昁梫偼側偄丅偙偺柦戣傪幃偱昞尰偡傟偽偄偄丅偦偆偡傞偲忦審幃偺偁傞幃偺徹柧偲側傞丅
亙傛偟偍亜偦偆偐丅乽俈偺攞悢偱偁傞乿傪乽俈偺攞悢偵摍偟偄乿偲傒傟偽偄偄偺偱偡偹丅偩偐傜丄
丂丂丂俀k+2亄俁2k+1亖俈俶丂(俶偼惍悢) 乧乧(*)
傪壖掕偟偰丄
丂丂丂俀(k+1)+2亄俁2(k+1)+1亖俈俶'丂(俶'偼惍悢)
傪徹柧偡傞偲偄偆偙偲偱偡偹丅
亙愭丂惗亜偱偼丄偙偙傜曈偱僶僩儞僞僢僠偟偰丄屻敿偼偐偢巕偵傗偭偰傕傜偍偆偐丅
亙偐偢巕亜乧乧愭惗丄巹偵傕僸儞僩傪偔偩偝偄丅
亙愭丂惗亜崱擔偼偢偄傇傫傒傫側偰偙偢偭偰偄傞偹丅忦審幃偺偁傞摍幃偺徹柧偩偐傜婎杮曽恓偼乽忦審幃偺幾杺幰傪徚偣乿偲偄偆偙偲偩傛丅傕偆彮偟丄暘偐傝堈偔偄偆側傜丄忦審幃偵偍偄偰丄
丂丂丂倎亖俀k+2丆倐亖俁2k+1
偲偍偄偰傒傟偽偄偄丅偡傞偲丄
丂丂丂俀(k+1)+2亖俀丒俀k+2亖俀倎丆俁2(k+1)+1亖俁2丒俁2k+1
俋倎
丂偩偐傜丄寢嬊丄
丂丂丂倎亄倐亖俈俶丂佀丂俀倎亄俋倎亖俈俶'
偺徹柧偲偄偆偙偲偩丅
亙偐偢巕亜偁偭丄愭惗丄傕偆偄偄偱偡丅偦偙偐傜偼偱偒傑偡丅忦審幃偐傜倎偐倐偺偳偪傜偐傪徚嫀偡傟偽偄偄傫偱偡偹丅
丂椺偊偽丄倐傪徚嫀偡傞偲丄倐亖俈俶亅倎傪摍幃偺嵍曈偵戙擖偟偰丄
丂丂丂俀倎亄俋倐亖俀倎亄俋乮俈俶亅倎乯
丂丂丂丂丂丂丂丂亖俇俁俶亄俈倎
丂丂丂丂丂丂丂丂亖俈(俋俶亄倎)
丂偙偙偱丄俶'亖俋俶亄倎偲偡傟偽丄徹柧偱偒傑偡丅
亙愭丂惗亜偙傟偱丄値亖倠亄侾偱徹柧偝傟偨偲偄偆偙偲偵側傞丅偦偟偰丄嵟屻偵乧乧
亙傑側傇亜偁偭丄杔偵傗傜偣偰偔偩偝偄丅値亖侾傪戙擖偟偰丄
丂丂丂乮梌幃乯亖俀3亄俁3亖俁俆
丂偩偐傜丄俈偺攞悢偱偡丅
亙愭丂惗亜埲忋傛傝丄偡傋偰偺帺慠悢偱柦戣偼惉棫偡傞偲偄偆偙偲偵側傞偹丅
丂偦傟偵偟偰傕丄傑側傇偼旤枴偟偄偲偙傠偽偐傝傕偭偰偄偔側丅
亙傑側傇亜偪傚偭偲怱奜偩側偁丅偦傟偠傖(2)偼丄杔偑夝偒傑偡丅
丂傑偢丄値亖倠偱惉棫偡傞偲壖掕偡傞丅
丂丂丂俀k亜俀倠亅侾丂乧乧(*)
丂偙傟傪忦審幃偲傒偰丄値亖倠亄侾偱惉棫偡傟偽偄偄偐傜丄
丂丂丂俀k+1亜俀(倠亄侾)亅侾
偺徹柧偲偄偆偙偲偱偡丅
丂晄摍幃偺徹柧偩偐傜嵍曈偐傜塃曈傪堷偄偰寁嶼偟偰傒傟偽偄偄丅
丂嵍曈偼俀k+1亖俀丒俀k偩偐傜丄忦審幃(*)傪晄摍幃偺宍偱戙擖偟偰丄幾杺幰偺俀k傪徚嫀偡傞偲丄
丂丂丂(嵍曈)亅(塃曈)亖俀丒俀k亅{俀(倠亄侾)亅侾}
丂丂丂丂丂丂丂丂丂丂亜俀(俀k亅侾)亅(俀倠亄侾)
丂丂丂丂丂丂丂丂丂丂亖俀倠亅俁
丂偝偰丄偁偲偼丄屻偼娙扨丅倠亞侾偩偐傜丄俀倠亅俁偑惓偺抣偵側偭偰偄傟偽乧乧乧丠丠丅
丂偁傟丄偍偐偟偄側丄惓偵側傜側偄傛丅偳偙偱娫堘偊偨傫偩傠偆丅偊偊偭偲乧乧丅
亙傛偟偍亜傑側傇丄寁嶼偼娫堘偭偰側偄傒偨偄偩傛丅偱傕丄倠亞侾側傜偽丄俀倠亅俁亞亅侾偩偐傜丄偙傟偠傖丄徹柧偱偒側偄丅晄巚媍偩側偁丅
亙偐偢巕亜幾杺幰偺埖偄偑偍偐偟偄傫偠傖側偄偐偟傜丅
亙傑側傇亜偳偆偄偆偙偲丅
亙偐偢巕亜忦審幃(*)偼丄
丂丂丂倎亖俀k丆倐亖俀倠
偲偍偔偲丄
丂丂丂倎亜倐亅侾丂乧乧(**)
偲偄偆偙偲傛偹丅偦偟偰丄偙傟傪棙梡偟偰丄
丂丂丂俀倎亜倐亄侾
傪徹柧偡傟偽偄偄傢偗偩偗偳丄愭傎偳丄傑側傇偼倎傪徚嫀偟偨偠傖側偄丅
幾杺幰傪倐偲傒偰徚偟偰傒偨傜偳偆偐偟傜丅
亙傛偟偍亜偲偵偐偔丄傗偭偰傒傛偆偐丅
(**)偺椉曈偺倎丆倐傪堏崁偟偰丄
丂丂丂亅倐亜亅倎亅侾
偙傟傪晄摍幃偺宍偱戙擖偟偰傒傛偆丅傛偭偰丄
丂丂丂俀倎亅(倐亄侾)亖俀倎亅倐亅侾
丂丂丂丂丂丂丂丂丂丂亜俀倎亄(亅倎亅侾)亅侾
丂丂丂丂丂丂丂丂丂丂亖倎亅俀
側傫偐丄椙偝偦偆偩傛丅
丂丂丂倎亅俀亖俀k亅俀
偩偐傜丄倠亞侾傛傝丄倎亅俀亞侽
傗偭偨丅値亖倠亄侾偱徹柧偱偒傑偟偨丅
亙愭丂惗亜偆傫丅偄偄僠乕儉儚乕僋偩偭偨偹丅偠傖偁丄値亖侾偵偮偄偰偼愭惗偑帵偦偆丅
丂丂丂(嵍曈)亅(塃曈)亖侾亜侽
偝偁丄姰惉偩丅
亙傑側傇亜愭惗丄偪傚偭偲傑偭偰傛丅側傫偐拠娫奜傟偵偝傟偨傛偆側婥偑偡傞傫偩偗偳丅杔偺峫偊偑摜傒偵偠偭偰偐偭偰偵榖傪恑傔偰偄傞傛偆側丅
亙偐偢巕亜側偵丄僆乕僷乕側偙偲偄偭偰傫偺傛丅旐奞栂憐偩傢丅
亙傑側傇亜傑偁丄偄偄傗丅偱傕偹丄傛偔峫偊傞偲杔偺夝摎偱傕徹柧偼壜擻偩偲巚偆傫偩偗偳側丅偩偭偰丄
丂丂丂(嵍曈)亅(塃曈)亜俀倠亅俁
偐傜丄倠亞俀偱偼俀倠亅俁亜侽偲側偭偰丄惉棫偡傞偙偲偼柧傜偐偩傛偹丅
亙傛偟偍亜偆傫丅
亙傑側傇亜偙偙偱丄値亖俀偺偲偒偼丄
丂丂丂(嵍曈)亅(塃曈)亖俀2亅(俀丒俀亅侾)亖侾亜侽
偱丄妋偐偵惉傝棫偮丅
偲偆偄偆偙偲偼丄悢妛揑婣擺朄偺尨棟偐傜値亞俀偱偼徹柧偑偱偒偨偲偄偆偙偲偱偼側偄偩傠偆偐丅
亙愭丂惗亜偍尒帠丅値亖侾偲偄偆僀儗僊儏儔乕傪奜偟偨偭偰偙偲偩側丅偦偟偰丄値亖侾偺応崌傪扨撈偵徹柧偟偰崌偣傟偽丄偡傋偰偺帺慠悢偱惉棫偟偨偲偄偊偹丅偍尒帠丅嶀偊偰傞偹丅
亙傑側傇亜嶰抜榑朄傒偨偄側悢妛揑婣擺朄偺徹柧偭偰丄側傫偐杔偺惈奿偵僼傿僢僩偡傞傫偩傛側丅
亙偐偢巕亜巹偼丄悢妛揑婣擺朄偭偰偆偝傫廘偔偰寵偩傢丅値亖倠偱惉棫偡傞偙偲傪壖掕偟偰丄徹柧偡傋偒偙偲傪徹柧偟偰偄傞偺傛丅偦偟偨傜偦偺壖掕偩偭偰偁傗傆傗偺傛偆側婥偑偡傞傢丅敀崟偼偭偒傝偟側偝偄偭偰姶偠傛丅暘偐傞丄傑側傇丅
亙傑側傇亜偐偢巕偵傖丄塱墦偲懕偔僪儈僲搢偟偺椃偺傛偆側丄抝偺儘儅儞偼暘偐傜側偄傛丅偹偭丄愭惗丅
亙愭丂惗亜婣擺朄偵僼傿僢僩偟偰偄傞傑側傇偺惈奿偼棟夝偟偨偔側偄偗偳偹丅
丂忦審幃偑晄摍幃偱偁傞応崌丄忦審幃傪徚嫀偡傞偲偄偆偙偲偼丄尨幃傪暿偺晄摍幃偱嬤帡偡傞偙偲偱偡偑丄偦偺嬤帡偑娚偗傟偽徹柧偑偱偒側偔側偭偰偟傑偆偙偲傕偁傞傢偗偱偡丅幚嵺丄傑側傇偺曽朄偱偼丄巜悢娭悢傪捈慄偵嬤帡偝偣傞傢偗偱偡偐傜丄悘暘備傞偄晄摍幃偵側偭偰偟傑偆偙偲偑暘偐傞偱偟傚偆丅
丂偦偙偱丄忦審幃傪嵟戝尷妶偐偦偆偲偡傞側傜丄
丂丂丂俹(倠)亜侽丂佀丂俹(倠亄侾)亜侽
傪帵偡偵偼丄
丂丂丂俹(倠亄侾)亜俹(倠)
傪徹柧偡傞偲峫偊偰傕偄偄偱偟傚偆丅
丂(2)偺応崌丄俹(倠)亖俀k亅(俀倠亅侾)偲偍偔偲丄
丂丂丂俹(倠亄侾)亅俹(倠)亖俀k+1亅(俀倠亄侾)亅{俀k亅(俀倠亅侾)}
丂丂丂丂丂丂丂丂丂丂丂丂亖俀k亅俀亞侽
丂丂丂丂亪丂俹(倠亄侾)亜俹(倠)亜侽
偲側傝傑偡丅
丂傑偨丄杮暥偱偼丄柦戣俹(値)偺徹柧偵偍偄偰俹(侾)偑恀偱偁傞偙偲傪嵟屻偵張棟偟偰偄傑偡丅傾儖僑儕僘儉揑偵偼俹(侾)偐傜徹柧偑弌敪偡傋偒側偺偱偟傚偆偑丄僪儈僲搢偟偲偺懳斾偐傜婣擺朄偺尨棟傪愢柧偡傞側傜偽丄
丂丂丂乽師偺僪儈僲偑搢傟傞傛偆偵暲傋偰偄偭偰丄嵟屻偵侾斣栚偺僪儈僲傪搢偡乿
偲峫偊偨曽偑姶妎揑偵偼暘偐傝堈偔側傝傑偡丅婣擺朄偺徹柧偼丄偐偢巕偑弎傋偰偄傞傛偆偵乽壖掕偟偨傕偺偱徹柧傪帋傒傞乿偺偱偡偑丄偦偺堘榓姶偼丄尰幚偵嵟屻偵搢偡偙偲偱夝徚偱偒傞傢偗偱偡丅
丂偲偙傠偱丄悢妛揑婣擺朄偺徹柧僾儘僙僗偼徹柧偺忬嫷偵崌偣偰僨僼僅儖儊偝傟傑偡丅偦偺婔偮偐偺宍懺傪埲壓偵怗傟偰傒傑偟傚偆丅
仜僲乕儅儖側悢妛揑婣擺朄
|
帺慠悢偵娭偡傞柦戣傪俹(値)偲偡傞偲偒丄 (嘥) 俹(侾)偑恀 (嘦) 俹(倠)偑恀側傜偽俹(倠亄侾)偑恀 (嘨) (嘥),(嘦)傛傝丂偡傋偰偺値偵懳偟偰俹(値)偼恀 |
丂(嘥)偵偮偄偰偼丄
丂丂丂(嘥) 俹(倰)丂乮倰亞侾乯
偲偱偒傑偡丅惉棫偺弌敪揰偺栤戣偵夁偓傑偣傫丅
仜椵愊宆悢妛婣擺朄
|
帺慠悢偵娭偡傞柦戣傪俹(値)偲偡傞偲偒丄 (嘥) 俹(侾)偑恀 (嘦) 俹(侾)丆俹(俀)丆俹(俁)丆丒丒丒丆俹(倠)偑恀側傜偽俹(倠亄侾)偑恀 (嘨) (嘥),(嘦)傛傝偡傋偰偺値偵懳偟偰俹(値)偼恀 |
仜暲楍宆悢妛婣擺朄
|
帺慠悢偵娭偡傞柦戣傪俹(値)偲偡傞偲偒丄 (嘥) 俹(侾)丆俹(俀)丆丒丒丒丆俹(倰)偑恀 (嘦) 俹(倠)丆俹(倠亄侾)丆俹(倠亄俀)丆丒丒丒丆俹(倠亄倰亅侾)偑恀側傜偽俹(倠亄倰)偑恀 (嘨) (嘥),(嘦)傛傝偡傋偰偺値偵懳偟偰俹(値)偼恀 |
倰亖俀偺応崌偼丄偙偺婣擺朄偺徹柧僷僞乕儞偼傛偔棙梡偝傟傑偡丅
|
ex) 俀師曽掱幃倶2亄倎倶亄倐亖侽乮倎丆倐伕倅乯偺俀夝傪兛丆兝偲偡傞偲偒丄 丂丂丂兛n亄兝n 偼惍悢偱偁傞偙偲傪徹柧偣傛丅 |
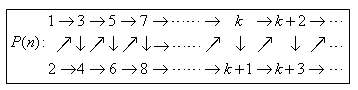 徹柧)
徹柧)
夝偲學悢偺娭學傛傝丄
丂丂丂兛亄兝亖亅倎丆兛兝亖倐
偙傟偐傜丄
丂丂丂兛2亄兝2亖(兛亄兝)2亅俀兛兝亖倎2亅俀倐
傛偭偰丄値亖侾丆値亖俀偺偲偒偼惉棫偡傞丅
師偵丄値亖倠丆値亖倠亄侾偱惉棫偡傞偲壖掕偡傞丅
兛k亄兝k丆兛k+1亄兝k+1偼惍悢偲偡傞偲丄
丂丂丂兛k+2亄兝k+2亖(兛k+1亄兝k+1)(兛亄兝)亅兛兝(兛k亄兝k)
丂丂丂丂丂丂丂丂丂亖亅倎(兛k+1亄兝k+1)亅倐(兛k亄兝k)
傛偭偰丄兛k+2亄兝k+2傕惍悢偱偁傞丅
埲忋傛傝丄偡傋偰偺帺慠悢値偱惉棫偡傞丅丂丂丂Q.E.D
摨條偵丄倰師曽掱幃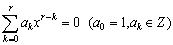 偺夝兛k (倠亖1,2,乧,r)偵懳偟偰丄
偺夝兛k (倠亖1,2,乧,r)偵懳偟偰丄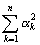 偑惍悢偱偁傞偙偲偼丄暲楍宆偺婣擺朄偵傛傝徹柧偝傟傑偡丅
偑惍悢偱偁傞偙偲偼丄暲楍宆偺婣擺朄偵傛傝徹柧偝傟傑偡丅
丂偙偺懠偺僷僞乕儞偲偟偰丄
仜擇廳宆悢妛婣擺朄
|
帺慠悢倣丆値偵娭偡傞柦戣傪俹(倣丆値)偲偡傞偲偒丄 (嘥) 俹(倣丆侾)丆俹(侾丆値)偑恀 (嘦) 俹(倣丆倠)丆俹(倢丆値)偑恀側傜偽俹(倣丆倠亄侾)丆俹(倢亄侾丆値)偑恀 (嘨) (嘥),(嘦)傛傝偡傋偰偺倣丆値偵懳偟偰俹(倣丆値)偼恀 |
仜戅峴宆悢妛婣擺朄(backword-induction)
|
帺慠悢値偵娭偡傞柦戣傪俹(値)偲偡傞偲偒丄 (嘥) 偁傞帺慠悢値偵懳偟偰俹(値)偑恀 (嘦) 俹(倣)偑恀側傜偽俹(倣亅侾)偑恀 (嘨) (嘥),(嘦)傛傝偡傋偰偺倣埲壓偺偡傋偰偺帺慠悢値偵懳偟偰俹(値)偼恀 |
丂偙偺婣擺朄偼丄椺偊偽憡壛丒憡忔暯嬒偺徹柧偵巊傢傟傑偡丅
倣亖俀k偺応崌偵偮偄偰偼丄悢妛揑婣擺朄偵傛傝娙扨偵徹柧偱偒傑偡丅偙偺倣偺壖掕偵懳偟偰丄倣亅侾傪徹柧偡傞偙偲偵傛傝丄偡傋偰偺帺慠悢偱憡壛丒憡忔暯嬒偺娭學偑帵偝傟傞傢偗偱偡丅
偲偙傠偱丄帺慠悢偺廤崌偵偼
仜挻尷婣擺朄
|
惍楍廤崌倃偵娭偡傞柦戣傪俹(倃)偲偡傞丅 丂丂丂擟堄偺倷(倷亙倶)偵懳偟偰丄俹(倷)佀俹(倶)偑惉棫偡傞 偲偒丄偡傋偰偺倶伕倃偵懳偟偰俹(倶)偑惉棫偡傞 |
丂悢妛揑婣擺朄偼偙偺傛偆偵丄偄傠偄傠側僷僞乕儞偑峫偊傜傟傞傢偗偱偡偑丄暿偺尒曽傪偡傟偽丄徹柧朄帺懱偑晄埨掕偱偁傞偲傕偄偊傑偡丅
丂悢妛揑婣擺朄偼丄嶰抜榑朄傪敪揥偝傟偨傕偺偱偡丅
丂嶰抜榑朄(僇僢僩朄)偼宍幃榑棟偵傛偭偰傾儕僗僩僥儗僗偑峫偊丄偦偺屻偺悢妛幰偵傛偭偰懱宯壔偝傟傑偡丅偦偟偰丄偦傟傪搚戜偵僪亅儌儖僈儞偑悢妛揑婣擺朄傪姰惉偝偣傑偡丅偝傜偵丄儁傾僲偺岞棟偺柍柕弬惈偐傜僎儞僣僃儞偼弴彉悢偵偍偗傞挻尷婣擺朄偺榑朄偵奼挘偟傑偟偨丅
丂悢妛揑婣擺朄偑帺慠悢偺嵟彫尨棟偐傜摼傜傟傞偺側傜丄挻尷婣擺朄偼帺慠悢埲奜偵嵟彫尨棟傪枮偨偡廤崌(惍楍廤崌)傪嶌傟側偄偐偲偄偆敪憐偐傜惗傑傟偨傢偗偱偡丅偙偺寢壥丄僎儞僣僃儞偼丄
丂丂丂嶰抜榑朄偱徹柧偱偒傞偙偲偼丄嶰抜榑朄傪巊傢側偔偰傕徹柧偱偒傞
偲偄偆僇僢僩徚嫀朄側傞寢榑偵偨偳傝拝偔偺偱偡丅
丂悢妛揑婣擺朄偼傾僉儗僗偲婽偺榖偺傛偆偵僷儔僪僢僋僗偺戙昞椺偲偟偰傛偔榖戣偵側傝傑偡丅柍尷夞偺嶰抜榑朄偲峫偊傟偽婲偙傝偊傞傢偗偱偡丅偦偆偄偭偨僷儔僪僢僋僗偺夝徚偺偨傔偵丄悢妛揑婣擺朄偼奼挘偝傟偨偲峫偊傞傋偒偱偟傚偆丅
丂側偍丄崱夞偺彫庤媄偼乽億傾儘偺挧愴乿側傞抁曇彫愢偲暲峴偟偰傑偲傔傑偟偨丅傛傠偟偗傟偽偦偪傜偺曽傕偛棗偔偩偝偄丅