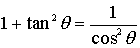 偭偰側偁偵
偭偰側偁偵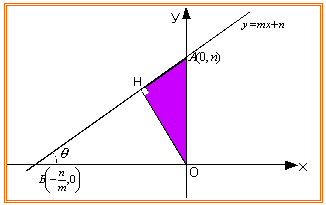 亙愭丂惗亜慜帪傑偱偼丄恾宍偺惈幙偺挷傋傞僣乕儖偱偁傞嶰庬偺恄婍偺偆偪丄
亙愭丂惗亜慜帪傑偱偼丄恾宍偺惈幙偺挷傋傞僣乕儖偱偁傞嶰庬偺恄婍偺偆偪丄亙傑側傇亜偼偄丄佢俙俷俫偱偡丅
亙愭丂惗亜偦偆偩偹丅偙偙偱嶰妏宍俙俷俫偼捈妏嶰妏宍偩偐傜丄媮傔傞俷俫偺挿偝偼嶰妏斾傪峫偊傞偲丄
丂丂丂俷俫亖俷俙cos兤
偱梌偊傜傟傑偡丅俷俙亖乥値乥偱偡偐傜丄俷俫亖乥値乥cos兤 丄偙傟偑媮傔傞悅慄偺挿偝偲偄偆偙偲偵側傝傑偡丅偲偙傠偱栤戣偼偙偺 偺抣偼側傫偩傠偆偐丅
亙惗丂搆亜丂乧乧乧
亙愭丂惗亜兤偺堄枴傪傛乕偔峫偊偰偛傜傫丅
亙傑側傇亜偊乕偲丄兤偼捈慄偲倶幉偺側偡妏偩偐傜丄乧乧丅
亙愭丂惗亜偦偆丄妏搙偑曄傢傞偲捈慄偺壗偑曄傢傞偺偩傠偆丅
亙傛偟偍亜捈慄偺孹偒偱偡偐丅
亙愭丂惗亜偦偺捠傝丄偱偼嶰妏斾偱孹偒(孹幬)傪昞偡傕偺偼側傫偩偭偨傠偆丅
亙偐偢巕亜僞儞僕僃儞僩偱偡丅
亙愭丂惗亜偦偆偩偹丅偩偐傜丄
丂丂丂tan兤亖倣
側傞娭學幃偑摼傜傟傞偹丅偩偄傇丄栚昗偵嬤偯偄偰偒偨丅偁偲偼丄僞儞僕僃儞僩傪僐僒僀儞偱昞尰偡傟偽偄偄偺偩偗傟偳丄偙傟偼埲慜丄嶰妏斾偺妛廗偱傗偭偨偺偩偗傟偳丄偲偆偡傟偽偄偄丄傑側傇丅
亙傑側傇亜偊偭丄偁偺偆丄朰傟傑偟偨丅
亙愭丂惗亜偱偼丄巚偄弌偟偰偛傜傫丅cos2兤亄sin2兤亖侾傪偪傚偭偲偄偠傟偽偍偟傑偄偩丅
亙傑側傇亜偦偆偐丄僞儞僕僃儞僩傪嶌傟偽偄偄傫偩偐傜丄椉曈傪cos2兤偱傢傞偲丄
丂丂丂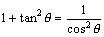
偲側傝傑偡丅
亙愭丂惗亜偦偺捠傝丅偝偁丄偙傟偐傜丄
丂丂丂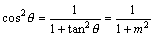
偲側傞偐傜丄 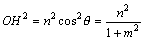 乧乧乧(*)
偱梌偊傜傟傞丅偢偄傇傫偒傟偄側幃偱昞尰偱偒偨偹丅
乧乧乧(*)
偱梌偊傜傟傞丅偢偄傇傫偒傟偄側幃偱昞尰偱偒偨偹丅
丂偱偼丄師偵丄(*)傪棙梡偟偰丄揰俙(倶1丆倷1)偲捈慄倷亖倣倶亄値偲偺嫍棧傪媮傔傛偆丅偙傟偼僇儞僞儞偩丅(*)傪巊偊傞傛偆偵掕揰偑尨揰偵側傞傛偆偵恾宍傪暯峴堏摦偡傟偽偄偄偩偗偩丅偱偼丄倶幉丄倷幉曽岦偵偳傟偩偗暯峴堏摦偝偣傟偽偄偄偩傠偆丅
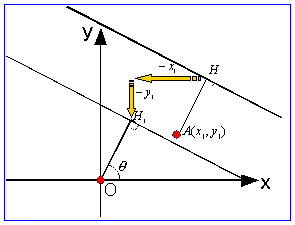 亙傛偟偍亜偼偄丄倶幉曽岦偵丄亅倶1丆倷幉曽岦偵亅倷1偱偡丅
亙傛偟偍亜偼偄丄倶幉曽岦偵丄亅倶1丆倷幉曽岦偵亅倷1偱偡丅
亙愭丂惗亜偦偆偡傞偲丄捈慄偺曽掱幃偼丄
丂丂丂倷亄倷1亖倣(倶亄倶1)亄値丂偡側傢偪丄倷亖倣倶亄倣倶1亅倷1亄値
偲側傞丅埲忋傛傝丄揰偲捈慄偺嫍棧俙俫偼丄
丂丂丂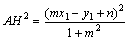 丂丂乧乧(**)
偲側傞偹丅
丂丂乧乧(**)
偲側傞偹丅
亙傑側傇亜愭惗丄側傫偩偐幃偑墭偔側偭偪傖偭偨傛偆偵巚偊傑偡偗偳丅
亙愭丂惗亜偦偆偩偹丅偱偼偙傟傪傕偆彮偟尒傗偡偔偟偰傒傛偆偐丅偄傑傑偱丄掕捈慄偼昗弨宍偱偁傜傢偟偨偗偳丄崱搙偼丄堦斒宍倎倶亄倐倷亄們亖侽偲偟偰昞尰偟偰傒傛偆丅偙傟傪岞幃偵揔梡偡傞偨傔偵丄孹偒偲倷愗曅傪媮傔偰偛傜傫丅
亙傛偟偍亜 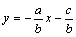 偱偡偐傜丄
偱偡偐傜丄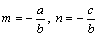 偱偡丅
偱偡丅
亙愭丂惗亜偱偼偙傟傪(**)偵戙擖偡傞偲丄
丂丂丂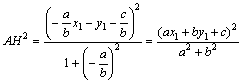
丂偳偆偩傠偆丅揰偲捈慄偺嫍棧偑丄偢偄傇傫偡偭偒傝偟偨岞幃偱傑偲傔傜傟偨偹丅
丂偦偙偱丄忋偺彫庤媄偱偼偦偙偺偲偙傠偵偙偩傢偭偰丄乽桳婡揑慻棫偰乿傪廳帇偟偰傑偲傔偰傒偨丅桳婡揑慻棫偰偲偼丄乽悢妛嘥乿偐傜乽悢妛嘦乿傊偺僗儉乕僘側嫶搉偟偺偙偲偱偁傞丅揰偲捈慄偺扨尦偼丄悢妛嘥偺嶰妏斾偺屻偵丄悢妛嘦偱埖傢傟傞偑丄庤朄偱偄偊偽丄屆棃偺婔壗揑偵恾宍偺惈幙傪挷傋傞偙偲偐傜丄恾宍傪僨僇儖僩嵗昗忋偵抲偒姺偊丄戙悢揑偵張棟偡傞傕偺偱偁傞丅偟偨偑偭偰丄巜摫偺棳傟偲偟偰傕嶰妏斾偺傕偮惈幙偑嵗昗忋偱偳偆昞尰偝傟傞偐偦偺寢傃偮偒偐傜揰偲捈慄偺娭學傪弎傋偨傎偆偑偄偄偺偱偼偲巚偆丅
丂椺偊偽丄俀捈慄偺悅捈忦審偵偮偄偰偼丄捈慄偲倶幉偺惓偺岦偒偲偑側偡妏傪兤偲偡傞偲丄悅捈側捈慄偲倶幉偲偺側偺妏偼兤亄兾/俀偱偁傞偐傜丄
丂丂丂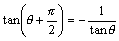
側傞娭學偑偊傜傟傞丅偙傟傪戙悢揑偵夝庍偡傞偲丄俀捈慄偺孹偒傪偦傟偧傟倣丆値偲偡傞偲丄
丂丂丂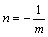
偲側傞傢偗偱偁傞丅摨條偵揰偲捈慄偺嫍棧偺岞幃偼丄y愗曅偑亇1偱丄孹偒偑tan兤偱偁傞捈慄偲尨揰偲偺嫍棧倓偱峫偊傞偲丄
丂丂丂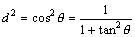
偱梌偊傜傟傞丅
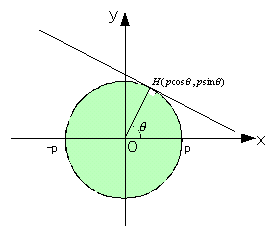 丂堦斒偵偼丄墌倶2亄倷2亖倫2偺墌廃忋偺揰丄俫(倫cos兤丆倫sin兤)偵偍偗傞愙慄偺曽掱幃(塃恾)丄
丂堦斒偵偼丄墌倶2亄倷2亖倫2偺墌廃忋偺揰丄俫(倫cos兤丆倫sin兤)偵偍偗傞愙慄偺曽掱幃(塃恾)丄
丂丂丂倶cos兤亄倷sin兤亖倫
傪捈慄偺惓婯曽掱幃(Hesse偺昗弨宍)偲偄偆偑丄偙偺偲偒尨揰偲捈慄偲偺嫍棧偼俷俫亖倫偱偁傞偐傜丄俹亖sin兤偺応崌偑忋弎偺嶰妏斾偺岞幃偵偁偨傞偙偲偑傢偐傞丅
丂偙偆偄偭偨攚宨傪摜傑偊偰丄揰偲捈慄偺嫍棧偺岞幃偼摫偐傟傞傋偒偱偼側偄偩傠偆偐丅
丂偲偙傠偱丄杮暥偺愢柧偼幚偼偢偄傇傫棎朶側偲偙傠偑偁傞丅偦傟偼丄捈慄偺曽掱幃傪
丂丂丂倷亖倣倶亄値丂丂丂(倣亜侽丆値亜侽)
偲惂尷偟偰偟傑偭偰偄傞偙偲偱偁傞丅倣亖侽丆倣亙侽丆値亖侽丆値亙侽偼丄堄幆揑(嶌堊揑)偵旔偗偰偄傞丅
丂偙傟偼丄岞幃傪價僕儏傾儖側僀儊乕僕偲偟偰偲傜偊偨偐偭偨偨傔偱偁傞丅
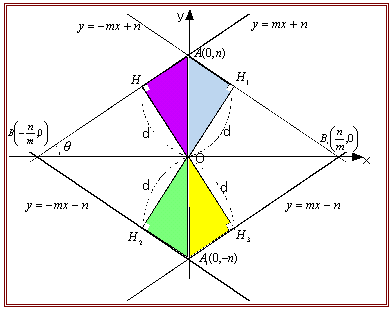 丂尩枾偵偼丄尨揰偲捈慄偺埵抲娭學偼嵍恾偺傛偆偵丄係偮偺case偑峫偊傜傟傞丅偙偺偦傟偧傟偵懳偟偰捈慄偑丄倶幉偺惓偺曽岦偲側偡妏兤傪愝掕偟偰嫍棧傪媮傔傞傢偗偱偁傞丅偟偐偟丄捈慄傪x幉懳徧丄y幉懳徧偟偰傕尨揰偲捈慄偺嫍棧偼晄曄偱偁傞傢偗偩偐傜丄侾偮偺応崌偩偗傪摫偗偽廫暘偱偁傠偆丅
丂尩枾偵偼丄尨揰偲捈慄偺埵抲娭學偼嵍恾偺傛偆偵丄係偮偺case偑峫偊傜傟傞丅偙偺偦傟偧傟偵懳偟偰捈慄偑丄倶幉偺惓偺曽岦偲側偡妏兤傪愝掕偟偰嫍棧傪媮傔傞傢偗偱偁傞丅偟偐偟丄捈慄傪x幉懳徧丄y幉懳徧偟偰傕尨揰偲捈慄偺嫍棧偼晄曄偱偁傞傢偗偩偐傜丄侾偮偺応崌偩偗傪摫偗偽廫暘偱偁傠偆丅
丂偙偙偺晹暘偺愢柧偼丄妛峑尰応偵偍偄偰尩枾惈偺嫋梕搙偑堎側傞傛偆偵巚偊傞偑丄懡偔偺妛峑偼丄杮暥偺愢柧偱帠懌傝傞偺偱偼側偄偩傠偆偐丅
丂側偍丄杮暥傪婰弎偟偨屻丄尰嵼弌斉偝傟偰偄傞嫵壢彂偱丄揰偲捈慄偺嫍棧傪恾宍揑偵夝庍偟偰偄傞傕偺偑側偄偐偲丄傆偲巚偄丄挷傋偰傒偨偲偙傠丄嬤擭弌斉偝傟偨丄俲彂揦偺愢柧偑丄捈妏嶰妏宍偺憡帡斾傪棙梡偟偨傕偺偱偁偭偨丅
彊乆偵偱偼偁傞偑丄悢妛嫵嵽偺帇妎壔偼丄怹摟偟偰偒偰偄傞偺偐傕偟傟側偄丅