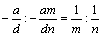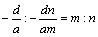亙傑側傇亜愭惗丆偳偆偟偨偺丏摢偱傕懪偭偨丏
亙愭丂惗亜恀柺栚側榖偩傛丏拑壔偝側偄傛偆偵丏傑偢丆師偺栤戣傪峫偊偰傒傛偆丏
|
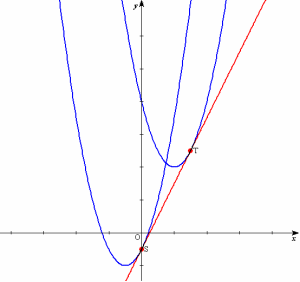
ex1) 師偺俀偮偺曻暔慄偺椉曽偵愙偡傞捈慄偺曽掱幃偲偦偺愙揰偺嵗昗傪媮傔傛丏 丂丂y亖x2亄2x亅1乧乧嘆丆 y亖x2亅4x亄8乧乧嘇 |
 亙偐偢巕亜 嫟捠愙慄偺掕斣偺栤戣偱偡偹丏愙慄偼y幉偵暯峴偱側偄偐傜愙慄偺曽掱幃傪y亖mx亄n偲偍偄偰丆敾暿幃傪巊偊偽偄偄傢丏巹偑夝偄偪傖偭偰偄偄偐偟傜丏傑偢丆嘆偲楢棫偝偣偰丆
亙偐偢巕亜 嫟捠愙慄偺掕斣偺栤戣偱偡偹丏愙慄偼y幉偵暯峴偱側偄偐傜愙慄偺曽掱幃傪y亖mx亄n偲偍偄偰丆敾暿幃傪巊偊偽偄偄傢丏巹偑夝偄偪傖偭偰偄偄偐偟傜丏傑偢丆嘆偲楢棫偝偣偰丆
丂丂丂x2亄(2亅m)x亅1亅n亖0丂乧嘊
敾暿幃傪D1偲偡傞偲丆
丂丂丂D1亖(2亅m)2亅4(亅1亅n)亖m2亅4m亄4n亄8亖0
師偵嘇偲楢棫偝偣偰丆
丂丂丂X2亅(4亄m)x亄8亅n亖0丂乧嘋
敾暿幃傪D2偲偡傞偲丆
丂丂丂D2亖(m亄4)2亅4(8亅n)亖m2亄8m亄4n亅16亖0
偙偺俀幃傪曈乆堷偄偰丆
丂丂丂亅12m亄24亖0丂傛偭偰丆m亖2
戞侾幃偵戙擖偟偰丆n亖亅1
埲忋傛傝丆y亖2x亅1
偦偟偰丆愙揰偼乧乧僷僗両丆傑側傇丆傗偭偰丏
亙傑側傇亜偍偄偍偄丆媫偵怳傞側傛丏傛偟偍偵僷僗両丏
亙傛偟偍亜偟傚偆偑側偄側丏m亖2傛傝丆嘊偺廳夝傪媮傔偰丆
丂丂丂x=(m-2)/2=0丂偙傟偐傜愙揰偼丆(0丆亅1)
摨條偵丆嘋偐傜愙揰偼丆(3丆2)丏
偱傕丆杔側傜栤戣偱偼愙揰傕梫媮偟偰偄傞偙偲傪峫偊傞偲丆旝暘傪巊偭偨曽偑偄偄偲巚偆側丏
亙愭丂惗亜偱偼丆傛偟偍丆尵偭偨愑擟傪偲偭偰夝偄偰傕傜偍偆丏
亙傛偟偍亜偼偄丆嘆偺愙揰偺x嵗昗傪x亖s偲偡傞偲丆
y'亖2x亄2傛傝丆愙慄偺曽掱幃偼丆
丂丂丂y亖(2s亄2)(x亅s)亄s2亄2s亅1亖(2s亄2)x亅s2亅1
摨條偵丆嘇偺愙揰偺x嵗昗傪x亖t偲偡傞偲丆
丂丂丂y亖(2t亅4)(x亅t)亄t2亅4t亄8亖(2t亅4)x亅t2亄8
俀幃偼堦抳偡傞偐傜丆
丂丂丂2s亄2亖2t亅4丆丂亅s2亅2亖亅t2亄8
丂丂丂亪丂s亖0丆t亖3丂
偙傟偐傜丆愙慄偲愙揰偑椉曽媮傔傜傟傑偡丏
亙愭丂惗亜偦偆偩偹丏偙偺俀偮偑戙昞揑側夝朄偩偹丏
亙傑側傇亜愭惗丆傕偆堦偮偁傞傛丏擇恖偺峫偊傪僪僢僉儞僌偝偣傞傫偩丏傛偟偍偑媮傔偨嘆偺愙慄偼丆
丂丂丂y亖(2s亄2)x亅s2亅1
偙傟偑嘇偲愙偡傟偽偄偄偐傜丆楢棫偝偣偰丆
丂丂丂x2亅(2s亄6)x亄s2亄9亖0
偙偺敾暿幃傪D偲偡傞偲丆
丂丂丂D/4亖(s亄3)2亅(s2亄9)亖6s亖0
偙傟偐傜丆s亖0偑媮傑傞丏
亙偐偢巕亜偄偮傕偺偙偲偩偗偳丆墳梡椡偲偄偆偐揔墳椡偲偄偆偐丆傑側傇偺僒僶僀僶儖婡擻偵偼嫲傟擖傞傢丏
亙傑側傇亜朖傔傜傟偰偄傞偲夝庍偟丆杔偺僒僶僀僶儖儗乕僟乕偱梊應偡傞偲丆愭惗偑尵偄偨偄偺偼偙傟偩偗偱偼側偄偱偡傛偹丏
亙愭丂惗亜傑偁偹丏幚偼偙偺栤戣偼丆愒偄昍傪巊偆偲丆侾暘偱偱偒偰偟傑偆丏
亙偐偢巕亜愒偄昍丠丆愙慄傕愙揰傕偱偡偐丠丏惁偄丏偳偆傗偭偰傗傞傫偱偡偐丏
亙愭丂惗亜偝偰丆庢傝弌偟偨傞愒偄昍丏
 亙傑側傇亜杮摉偵愒偄昍傪帩偭偰偄傞傫偱偡偐丏梡堄廃摓偲偄偆偐丏
亙傑側傇亜杮摉偵愒偄昍傪帩偭偰偄傞傫偱偡偐丏梡堄廃摓偲偄偆偐丏
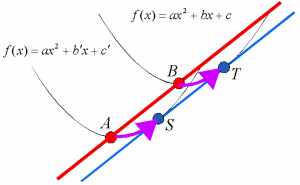
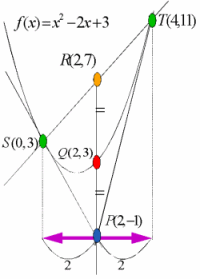
亙愭丂惗亜偍傎傫丆偝偰丆偙偺昍偺椉抂傪愙揰偵抲偔丏偦偆偟偰丆椉抂偑嬋慄忋偵偁傞傛偆偵丆嘆忋偺昍傪摦偐偟偰偄偔偲壗偐婥偑偮偔偙偲偼側偄偩傠偆偐丏
亙傑側傇亜側傫偐柺敀偦偆偩側丏杔偵傗傜偣偰丏偊乕偭偲丆偙偆嘆偺忋傪昍傪妸傜偡偲丆嘇傕摦偄偰乧丆偁偭丆暘偐偭偨偧丏
亙偐偢巕亜捀揰偩傢丏嘆偺捀揰偺埵抲偵昍偺抂偑偒偨偲偒丆嘇傕捀揰偵昍偺抂偑棃傞傢丏
亙傑側傇亜墶庢傝偡傞側傛丏偱傕峫偊偰傒傟偽摉偨傝慜偩傛側丏嘇偲嘆偺僌儔僼偼摨偠奐偒偩偐傜暯峴堏摦偟偨傜廳側傞丏偟偨偑偭偰昍偺挿偝偑屌掕偝傟偰偄偨傜丆嘆偲嘇偺嬋慄忋偺揰偺堏摦検偼摍偟偄偲偄偆偙偲偱偡傛偹丏
亙愭丂惗亜偦偆丆媡偵捀揰偺埵抲偐傜堏摦偝偣偰傒傟偽傕偭偲暘偐傝傗偡偄丏彮偟偢偮嬋慄忋傪偢傜偟偰偄偔偲丆愙慄偵側傞丏
亙傛偟偍亜偦偆偐丆偲偄偆偙偲偼愭惗丆昍偼暯峴堏摦偟偰偄傞傢偗偩偐傜丆愙慄偺孹偒偲俀捀揰傪寢傇慄暘偺孹偒偼摍偟偄偲偄偆偙偲偵側傝傑偡偹丏
亙愭丂惗亜偦偺捠傝丏偦傟偧傟偺曻暔慄傪昗弨宍偵偡傞偲丆
丂丂丂y亖(x亄1)2亅2丆 y亖(x亅2)2亄4
傛偭偰丆俀捀揰(亅1丆亅2)丆(2丆4)傪寢傇慄暘偺孹偒偼丆
丂丂丂m={4亅(亅2)}/{2亅(亅1)}=2
嘆傛傝丆y'亖2x亄2傛偭偰丆愙揰偺x嵗昗偼丆2x亄2亖2傛傝丆x亖0
偙傟偐傜丆愙揰偼(0丆亅1)傛傝丆愙慄偺曽掱幃偼丆y亖2x亅1
摨條偵丆嘇傛傝丆y'亖2x亅4亖2丂偙傟偐傜愙揰偼丆(3丆5)偲側傞丏
亙偐偢巕亜傎傫偲偩丏侾暘偖傜偄偱偱偒偪傖偭偨丏偱傕丆愭惗丆傂傚偭偲偟偨傜崱擔偺僱僞偼偙傟偩偗偠傖側偄偺偱偼丏
亙愭丂惗亜偐偢巕丆偦偺恖傪媈傞傛偆側娽偮偒偼丆傑側傇偑擖偭偰偧丏偳偆偟偰丆偦偆巚偆傫偩偄丏
亙偐偢巕亜偙傟偩偗偺偙偲偵偢傏傜側愭惗偑傢偞傢偞昍傪梡堄偡傞傢偗側偄偟丆偦傟偲崱夞偺僥乕儅偑嫟捠愙慄側傜丆傕偆堦偮暿偺嫟捠愙慄偑峫偊傜傟傞偲巚偆偺偩偗傟偳丏
亙愭丂惗亜昍傪梡堄偟偰偒偨偙偲偺壇應偼梋寁側偍悽榖偩偗偳丆傕偆堦偮偺嫟捠愙慄偵婥偑偮偄偨偺偼塻偄丏師偺栤戣傪尒偰偛傜傫丏
|
ex2) 師偺俀偮偺曻暔慄偺嫟捠愙慄偺曽掱幃傪媮傔傛丏 丂丂丂y亖x2亅2x亄3丂乧嘆丆丂y亖亅x2亄6x亅13丂乧嘇 |
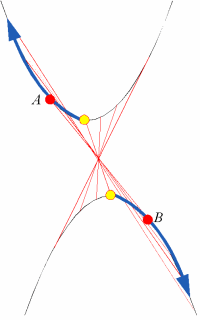 亙傑側傇亜偦偆偐丆曻暔慄偺僌儔僼偺奐偒偑忋偵撌偲壓偵撌偺応崌偐丏側傞傎偳丆偙偺応崌偺嫟捠愙慄傕偁傝偊傞偐丏
亙傑側傇亜偦偆偐丆曻暔慄偺僌儔僼偺奐偒偑忋偵撌偲壓偵撌偺応崌偐丏側傞傎偳丆偙偺応崌偺嫟捠愙慄傕偁傝偊傞偐丏
亙傛偟偍亜偙傟偼俀偮偺愙慄偑峫偊傜傟傑偡偹丏崱擔偺僥乕儅偐傜峫偊傞偲丆偙傟傕愒偄昍傪巊偆偲偱偒傞偲偄偆偙偲偵側傝傑偡偹丏
亙愭丂惗亜傛偟偍傕愭撉傒偡傞傛偆偵側偭偨偐丏傑側傇僂傿儖僗偑枲墑偟偨偐側丏
傑偁丆僂傿儖僗偵姶愼偟偨彅孨側傜傕偆暘偐偭偰偄傞偲巚偆偗偳丆摉慠傑偢俀捀揰傪寢傇丏偦偆偟偰丆嫟捠愙慄偵側傞傛偆偵堏摦検傪摨偠偵偟偰嬋慄忋傪偢傜偟偰偄偔傫偩偗偳丆壓偵撌偺曻暔慄忋偺揰傪嵍曽岦偵摦偐偡偲丆忋偵撌偺曽偼塃曽岦偵側傞偹丏偩偐傜昍傪怢偽偟側偑傜摦偐偡偙偲偵側傞丏幚墘偟傛偆丏偙偆偩丏偙偺摦偒傪傒偰壗偐姶偠傞偙偲偼側偄偐側丏
亙偐偢巕亜偡偩傟傪偹偠偭偨宍偵昍偺婳愓偑弌棃忋偑傞傢丏
亙傑側傇亜偲偄偆偙偲偼丆偦偺偹偠偭偨売強偼掕揰偲偄偆偙偲偵側傜側偄偐側丏
亙傛偟偍亜偦傟偼昍偺拞揰偱偡傛偹丏
亙愭丂惗亜楢學僾儗僀偲偄偆傛傝擇恖偑傑側傇偺僋儘乕儞偵側偭偰偄傞傛偆偱偪傚偭偲晐偄偑丆偦偺捠傝偩丏偙傟傕峫偊偰傒傟偽摉偨傝慜偩偹丏俀偮偺曻暔慄傪廳偹傞偵偼俀捀揰偺拞揰偵娭偟偰懳徧堏摦偡傟偽偄偄傢偗偩偐傜丏
亙傑側傇亜偦偆偐丏偲偄偆偙偲偼丆愙慄傕偙偺拞揰傪捠傞偭偰偙偲偩丏
亙偐偢巕亜偩偐傜丆揰偑偒傑偭偰偄傞偐傜屻偼孹偒傪媮傔傟偽偄偄偭偰偙偲偹丏
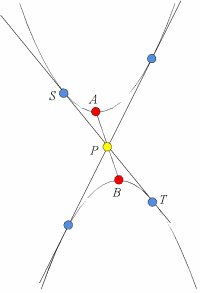 亙傛偟偍亜偁傞偄偼旝暘偱愙揰傪媮傔傞丏
亙傛偟偍亜偁傞偄偼旝暘偱愙揰傪媮傔傞丏
亙愭丂惗亜傑偁丆偦偆偄偆偙偲偩丏偠傖丆扤偐媮傔偰偛傜傫丏
亙偐偢巕亜傑偢嘆偺捀揰偼丆y亖(x亅1)2亄2傛傝丆A(1丆2)丏
摨條偵嘇偼丆y亖亅(x亅3)2亅4傛傝丆B(3丆亅4)
偟偨偑偭偰拞揰偼P(2丆亅1)偩傢丏
亙傛偟偍亜偁偲偼丆敾暿幃偐旝暘傪巊偊偽偄偄偱偡偹丏旝暘偱傗傝傑偡丏
嘆偺愙揰偺x嵗昗傪x亖t偲偍偔偲丆愙慄偺曽掱幃偼丆
丂丂丂y亖(2t亅2)(x亅t)亄t2亅2t亄3亖(2t亅2)x亅t2亄3丂乧(*)
偙傟偵揰P傪戙擖偟偰丆亅1亖2(2t亅2)亅t2亄3
丂丂丂t2亅4t亖0傛傝丆t亖0丆4
偟偨偑偭偰丆(*)幃偵戙擖偟偰丆y亖亅2x亄3丆y亖6x亅13
偲側傝傑偡丏
亙傑側傇亜偆乕傫丆側傫偲側偔偱偒偨偗偳丆偟偭偔傝偙側偄側偁丏
亙偐偢巕亜壗偑側偺丏娙扨偵媮傑偭偰傞偠傖側偄丏
 亙傑側傇亜妋偐偵晛捠偵傗傞傛傝娙扨偩偗偳丆嵟弶偵傗偭偨僌儔僼偺奐偒偑摨偠応崌偺侾暘偺夝摎偵斾傋傞偲悘暘庤娫偑偐偐偭偰偄傞婥偑偟側偄偐丏
亙傑側傇亜妋偐偵晛捠偵傗傞傛傝娙扨偩偗偳丆嵟弶偵傗偭偨僌儔僼偺奐偒偑摨偠応崌偺侾暘偺夝摎偵斾傋傞偲悘暘庤娫偑偐偐偭偰偄傞婥偑偟側偄偐丏
亙傛偟偍亜偦偆偄偊偽丆偦偆偩側丏
亙愭丂惗亜偝偡偑丆尦僂傿儖僗傑側傇丏偡傞偳偄丏
亙傑側傇亜傂偱偉側丏愭惗丆傑偩旈枾傪塀偟帩偭偰傞偱偟傚丏憗偔揻偒側傛丏
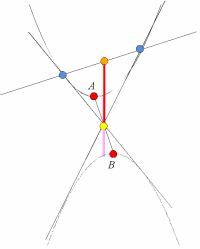
亙愭丂惗亜偦傟偱偼丆偝偰丆偙偺愒偄昍偺椉抂傪 幉偵暯峴偵側傞傛偆偵曻暔慄傪堏摦偝偣傞丏偙偺偲偒偺昍偺挿偝偱壗偐婥偯偔偙偲偼丏
亙惗搆払亜乧乧乧
亙愭丂惗亜偱偼丆昍偺壓抂偑拞揰P偵側傞傛偆偵昍傪忋偵暯峴堏摦偝偣傞偲乧丏
亙偐偢巕亜偁偭丆愭惗丆傢偨偟抦偭偰傞丏壓偵撌偺曻暔慄偺俀愙揰傪寢傇偲丆愒偄昍偺忋抂偼偦偺捈慄忋偵偁傞傫偱偟傚丏
亙傑側傇亜偦傫側惈幙偁傞偺丏
亙愭丂惗亜曻暔慄偺戝帠側惈幙偺傂偲偮偩偹丏
捈姶揑側徹柧偼愒偄昍偲曻暔慄偑岎傢偭偨揰Q偵偍偗傞愙慄傪媮傔偰丆愙慄偺抣偩偗曻暔慄偺抣傪堷偄偰傒傞丏
亙傑側傇亜愭惗偺摼堄側y幉偵暯峴偵嬋慄傪僗儔僀僗偟偰x幉忋偵惍宍偟側偍偡偭偰曽朄偱偡偹丏
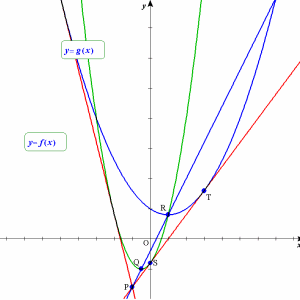
亙愭丂惗亜偦偆丆僗働乕儕儞僌偲偄偭偨偹丏偦偆偡傞偲偙偺曻暔慄偼揰Q傪捀揰偲偡傞曻暔慄偺婎杮宍偵惍宍偱偒傞丏偙偺恾偐傜曻暔慄偵娭偡傞偄傠偄傠側惈幙偑尒偊偰偔傞丏椺偊偽俀愙揰偺x嵗昗偺暯嬒偼丆揰P偺x嵗昗偵摍偟偄偙偲偐傜丆惍宍偟偨慄暘ST偼x幉偵暯峴偲側傞丏偙傟偼傕偲偺曻暔慄偵偍偄偰揰Q傪捠傞愙慄偲丆捈慄ST偼暯峴偱偁傞偙偲傪堄枴偡傞丏
亙傛偟偍亜慄暘ST偲曻暔慄偱埻傑傟傞恾宍偺柺愊S1偲丆俀愙慄偲曻暔慄偱埻傑傟傞恾宍偺柺愊S2偺柺愊斾偼丆
丂丂丂S1丗S2亖2丗1
偵側傞偭偰偄偆偺傕偁傝傑偟偨傛偹丏
亙愭丂惗亜偦偟偰偙傟傜偺惈幙傪巊偆偲ex偺栤戣傕娙扨偵夝偗偰偟傑偆傫偩丏
偦偺慜偵彮偟傕偲傕偲偺栤戣傪惍棟偟偰傒傛偆丏
傑偢丆俀偮偺曻暔慄偺捀揰傪寢傇慄暘偺拞揰偵娭偟偰俀偮偺曻暔慄偼懳徧偱偁傞偙偲偑暘偐偭偨丏偦偺懳徧揰P(2丆亅1)傪捠傞愙慄傪媮傔傞偲峫偊傟偽ex2偺栤戣偼丆
| ex3) 揰P(2丆亅1)偐傜曻暔慄y亖x2亅2x亄3偵堷偄偨愙慄傪媮傔傛丏 |
偲傒側偡偙偲偑偱偒傞偩傠丏
 亙偐偢巕亜側傫偩丏嫟捠愙慄偺栤戣偲丆嬋慄奜偐傜堷偄偨愙慄偺栤戣偼摨偠偙偲傪梫媮偟偰偄偨傫偱偡偹丏偱傕丆偙偺応崌偺媮傔曽傕丆捠忢偼丆愙揰傪揔摉偵偍偄偰愙慄偺曽掱幃傪嶌傝丆嬋慄奜偺揰傪戙擖偡傞偭偰曽朄偩偭偨偲巚偆偗偳丏
亙偐偢巕亜側傫偩丏嫟捠愙慄偺栤戣偲丆嬋慄奜偐傜堷偄偨愙慄偺栤戣偼摨偠偙偲傪梫媮偟偰偄偨傫偱偡偹丏偱傕丆偙偺応崌偺媮傔曽傕丆捠忢偼丆愙揰傪揔摉偵偍偄偰愙慄偺曽掱幃傪嶌傝丆嬋慄奜偺揰傪戙擖偡傞偭偰曽朄偩偭偨偲巚偆偗偳丏
亙傑側傇亜偩偐傜丆偦傟偑娙扨偵偱偒偰偟傑偆偲偄偆偙偲傪愭惗偼偄偄偨偄傫偱偟傚丏
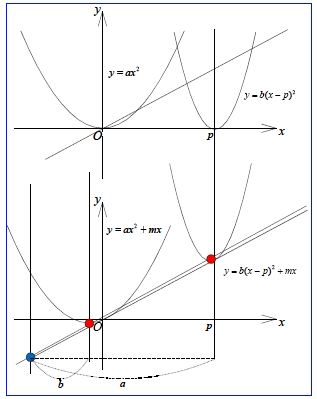
亙愭丂惗亜偦偆偄偆偙偲偩丏偦偺偨傔偵偝偒傎偳偐偢巕偑偄偭偰偨惈幙傪恾偱愢柧偟偰偍偙偆丏
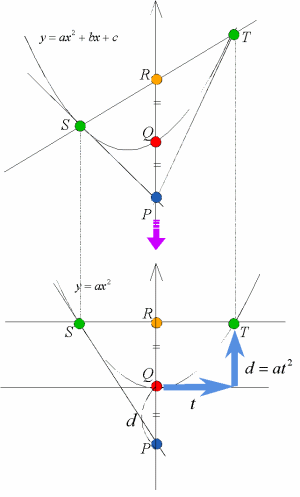
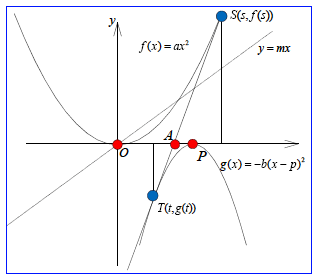
塃恾偵偍偄偰丆揰Q偵偍偗傞愙慄傪搚戜偵y幉曽岦偵僗働乕儕儞僌偟偰偱偒偨曻暔慄傪y亖ax2偲偡傞丏偙偺曻暔慄傪傒傞偲丆PQ亖QR偱偁傞偙偲偼偡偖偵暘偐傞丏
亙傑側傇亜偊偭丆偳偆偟偰丏
亙愭丂惗亜揰T(t丆at2)偵偍偗傞愙慄傪媮傔偰偛傜傫丏
亙傛偟偍亜 y'亖2ax偱偡偐傜丆愙慄偺曽掱幃偼丆
丂丂丂y亖2at(x亅t)亄at2亖2atx亅at2
偲側傝傑偡丏
亙愭丂惗亜媮傔傞俀愙慄偼丆曻暔慄y亖ax2偺y幉忋偺揰P(0丆亅at2)偐傜堷偄偨愙慄偵懳墳偟偰偄傞丏偙偙偱y愗曅at2偼丆y亖ax2偺尨揰偐傜偺x偺憹暘t偵懳偡傞y偺憹暘偵摍偟偄偙偲偐傜PQ亖QR偱偁傞偙偲偑暘偐傞丏
亙傑側傇亜側傞傎偳偹丏偦傟傪暦偄偰愭惗偑尵偄偨偄偙偲偑側傫偲側偔撉傔偰偒偨偧丏愭惗偼丆y偺憹暘偑暘偐傟偽丆愙揰偺x嵗昗偑偙偺惈幙傪巊偆偲媮傔傜傟傞偭偰偄偄偨偄傫偱偟傚偆丏
亙愭丂惗亜偝偡偑尦僂傿儖僗乧
亙傑側傇亜暘偐偭偨偐傜榖傪恑傔偰傛丏
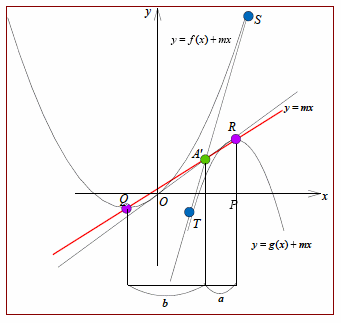
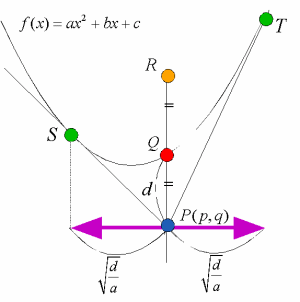 亙愭丂惗亜偦傟偱偼丆曻暔慄傪f(x)亖ax2亄bx亄c(a>0)偲偟丆揰P(p丆q)偐傜堷偄偨愙慄傪媮傔偰傒傛偆丏傑偢丆揰P傪捠傞y幉偵暯峴側捈慄x亖p偲曻暔慄偍傛傃俀愙慄ST傪寢傇慄暘偲偺岎揰傪偦傟偧傟Q丆R偲偡傞丏
亙愭丂惗亜偦傟偱偼丆曻暔慄傪f(x)亖ax2亄bx亄c(a>0)偲偟丆揰P(p丆q)偐傜堷偄偨愙慄傪媮傔偰傒傛偆丏傑偢丆揰P傪捠傞y幉偵暯峴側捈慄x亖p偲曻暔慄偍傛傃俀愙慄ST傪寢傇慄暘偲偺岎揰傪偦傟偧傟Q丆R偲偡傞丏
Q(p丆f(p))傛傝慄暘PQ偺挿偝d偼丆d亖f(p)亅q丏偙偙偱丆PQ亖QR偱偁傞偙偲傛傝丆QR亖d
師偵揰Q偵偍偗傞愙慄偱曻暔慄傪僗働乕儕儞僌傪偡傞偲丆曻暔慄偼y亖ax2偲傒側偣丆S丆T偺y嵗昗偼丆R偺y嵗昗偵摍偟偔側傞丏偡側傢偪丆
丂丂丂d亖ax2
偙傟偐傜丆
丂丂丂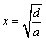 丏
丏
偙傟偑丆揰P偐傜S丆T傑偱偺x偺憹暘偵側傞傢偗偩丏偲偄偆偙偲偼丆S丆T偺x嵗昗偼偳偆昞偝傟傞偩傠偆偐丏
亙傛偟偍亜傕偲傕偲P(p丆q)偩偭偨偐傜丆
丂丂丂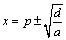
偲側傝傑偡偹丏惁偄丆媮傑傝傑偟偨丏愙揰偺x嵗昗偑偱傟偽偁偲偼娙扨偱偡傕偺偹丏
亙傑側傇亜傛偆偟丆偱偼愭惗偺婇傒傪娕攋偟偨彫惗偑ex3傪夝偄偰恑偤傛偆.
傑偢丆y亖f(x)偲偍偔偲丆f(2)亖3丆傛偭偰丆y偺憹暘偼丆3亅(亅1)亖4
偙傟偐傜x偺憹暘偼丆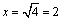 丏偟偨偑偭偰愙慄偺x嵗昗偼
丏偟偨偑偭偰愙慄偺x嵗昗偼
丂丂丂x亖2亇2亖0丆4
偁偲偼丆偐偢巕偵僶僩儞僞僢僠丏
 亙偐偢巕亜旤枴偟偄偲偙傠偽偭偐傝偮傑傒怘偄偡傞傫偩偐傜丏偟傚偆偑側偄傢偹丏
亙偐偢巕亜旤枴偟偄偲偙傠偽偭偐傝偮傑傒怘偄偡傞傫偩偐傜丏偟傚偆偑側偄傢偹丏
y'亖2x亅2偱丆揰(2丆亅1)傪捠傞愙慄偩偐傜丆
丂丂丂x亖0偺偲偒丆y亖亅2(x亅2)亅1亖亅2x亄3
丂丂丂x亖4偺偲偒丆y亖6(x亅2)亅1亖6x亅13
傎傫偲丆偁偭偲偄偆娫偵偱偒偰偟傑偆傫偱偡偹丏
亙傑側傇亜曻暔慄偺愨懳抣偺奐偒偑摨偠偭偰偙偲偼丆俀偮偺曻暔慄偼晇晈傒偨偄側傕偺側傫偩傠偆側丏擇恖偼愒偄昍偱寢偽傟偰偄偰丆曅曽偑摦偗偽摨偠傛偆偵偦傟偵廬偭偰傕偆曅曽偑摦偔丏偦偟偰偄偮傕捀揰偱曕挷傪偲傝偁偭偰偄傞傫偩丏傑偁丆晈彞晇悘偭偰偙偲偐側丏
亙偐偢巕亜傗偩偁丆傑側傇偭偨傜丆偄偮傕偺愭惗偺傑偲傔丆扗偭偪傖偭偰傞丏偱傕丆傑側傇丆晛捠丆墢傪寢傇偺偼丆愒偄昍偱側偔丆愒偄巺偭偰偄傢側偄丏
亙愭丂惗亜俀恖傪寢傫偱偄傞偺偑愒偄巺偲昍偱偼悘暘堘偆偩傠偆側丏僸儌偩偲丆側傫偐抝偼彈偵偔偭偮偄偰偄傞僌僂僞儔幰偺傛偆側報徾傪庴偗偰偟傑偆丏傕偆堦偮丏傑側傇偼丆乽晈彞晇悘乿偭偰偄偭偰偄偨偗偳丆杮摉偺偙偲傢偞偼丆乽晇彞晈悘乿丆晇偑彞偊偨偙偲偵嵢偑偟偨偑偆偲偄偆偙偲偩丏偱傕傑側傇偑偄偆偲丆愒偄僸儌傕丆晈彞晇悘傕尵梩偲偟偰偼惓偟偄偺偐傕偟傟側偄偗偳側丏
亙傑側傇亜傫乧乧丠
 丂崱夞偼奐偒(2師偺崁偺學悢)偺愨懳抣偑摍偟偄曻暔慄偺僌儔僼偺嫟捠愙慄傪庢傝忋偘傑偟偨偑丆奐偒偑堘偆応崌偼偳偆側傞偩傠偆偐丏捀揰傪寢傇慄暘偲偺娭學偵偮偄偰挷傋偰傒傛偆丏
丂崱夞偼奐偒(2師偺崁偺學悢)偺愨懳抣偑摍偟偄曻暔慄偺僌儔僼偺嫟捠愙慄傪庢傝忋偘傑偟偨偑丆奐偒偑堘偆応崌偼偳偆側傞偩傠偆偐丏捀揰傪寢傇慄暘偲偺娭學偵偮偄偰挷傋偰傒傛偆丏
 丂師偵丆f(x)丆g(x)偺x幉偱側偄嫟捠愙慄傪y亖mx偲偟丆偙傟傪俀偮偺曻暔慄偺抣偵壛偊丆y亖f(x)亄mx丆y亖g(x)亄mx傪嶌傞(偄傢備傞榓娭悢傪峫偊傞)丏
丂師偵丆f(x)丆g(x)偺x幉偱側偄嫟捠愙慄傪y亖mx偲偟丆偙傟傪俀偮偺曻暔慄偺抣偵壛偊丆y亖f(x)亄mx丆y亖g(x)亄mx傪嶌傞(偄傢備傞榓娭悢傪峫偊傞)丏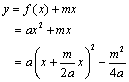
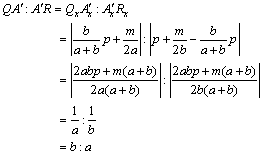
|
俀偮偺曻暔慄偺俀師偺崁偺學悢傪a丆亅b (a亜0丆b亜0)偲偡傞偲偒丆 嫟捠愙慄偺岎揰偼丆侾偮偺愙慄偵懳偡傞俀偮偺曻暔慄偺偦傟偧傟偺愙揰傪寢傇慄暘傪b丗a偺斾偵撪暘偡傞揰偱偁傞丏 |
丂傑偨丆忋弎偺徹柧夁掱偵偍偄偰丆
丂丂丂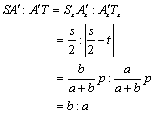
丂偙傟偐傜
|
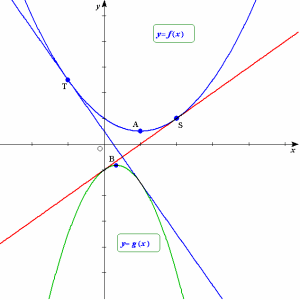
俀偮偺曻暔慄f(x)丆g(x)偺俀師偺崁偺學悢傪a丆亅b (a亜0丆b亜0)偲偡傞偲偒丆 嫟捠愙慄偺岎揰偼丆俀偮偺曻暔慄f(x)丆g(x)偺捀揰傪寢傇慄暘傪b丗a偺斾偵撪暘偡傞揰偱偁傞丏 |
|
ex1)師偺俀偮偺曻暔慄偺嫟捠愙慄偺曽掱幃傪媮傔傛丏 丂丂丂f(x)亖x2亅2x亄2丆g(x)亖亅3x2亄2x亅2 |
夝)
f(x)亖(x亅1)2亄1傛傝丆捀揰A(1丆1)
g(x)亖亅3(x亅1/3)2亅5/3傛傝丆捀揰B(1/3丆亅5/3)
傛偭偰丆慄暘AB傪3丗1偺斾偵撪暘偡傞揰偼丆P(1/2丆亅1)
f(1/2)亅(亅1)亖9/4傛傝丆愙揰偺x嵗昗偼丆x亖1/2亇3/2亖2丆亅1
f'(x)亖2x亅2偱偁傞偐傜丆愙慄偺曽掱幃偼丆
丂丂丂y亖2x亅2丆y亖亅4x亄1
 丂俀偮偺曻暔慄偺曽掱幃傪
丂俀偮偺曻暔慄偺曽掱幃傪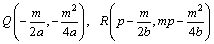
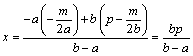
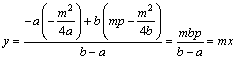
|
俀偮偺曻暔慄偺俀師偺崁偺學悢傪a丆b乮a亜0丆b亜0丆a亗b乯偲偡傞偲偒丆 俀捀揰傪寢傇慄暘偍傛傃俀愙揰傪寢傇慄暘傪b丗a偺斾偵奜暘偡傞揰偼堦抳偡傞丏 |
偑惉棫偡傞丏
|
ex2)師偺俀偮偺曻暔慄偺嫟捠愙慄偺曽掱幃傪媮傔傛丏 丂丂丂f(x)亖4x2亄8x亅16丆g(x)亖x2亅4x亄20 |
夝)
f(x)亖4(x亄1)2亅20傛傝捀揰Q(亅1丆亅20)
g(x)亖(x亅2)2亄16傛傝捀揰R(2丆16)
慄暘QR傪1丗4偺斾偵奜暘偡傞揰A(x丆y)偼丆
丂丂丂x亖(亅4亅2)/(亅1亄4)亖亅2丆倷亖(亅80亅16)/(亅1亄4)亖亅32
傛偭偰丆A(亅2丆亅32)
f(亅2)亅(亅32)亖16亖4丒22偱偁傞偐傜丆
愙揰偺x嵗昗偼丆
丂丂丂x亖亅2亇2
傛傝愙揰偼丆(0丆亅16)丆(亅4丆16)
埲忋傛傝丆嫟捠愙慄偼丆y亖8x亅16丆y亖亅24x亅80
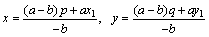 傛傝
傛傝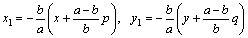
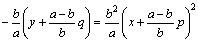
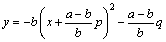
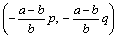 偱偁傞曻暔慄
偱偁傞曻暔慄
|
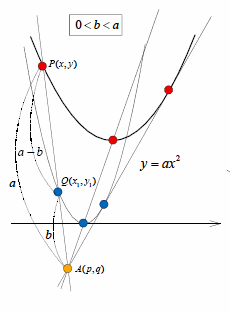
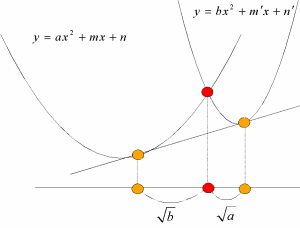
俀偮偺曻暔慄 丂丂丂y亖ax2亄mx亄n丆y亖bx2亄m'x亄n' 偺俀捀揰丆媦傃嫟捠愙慄偺俀愙揰傪寢傇慄暘傪亅b丗a偺斾偵暘偗傞揰偼堦抳偡傞丏 |
 丂丂
丂丂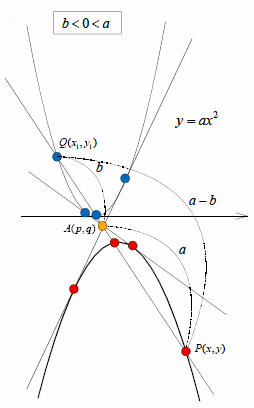
 丂俀偮偺曻暔慄
丂俀偮偺曻暔慄
|
俀偮偺曻暔慄 丂丂丂y亖ax2亄mx亄n丆y亖bx2亄m'x亄n (a亜0丆b亜0)) 偺岎揰偺x嵗昗偼丆偦傟偧傟偺曻暔慄偺愙揰傪寢傇慄暘偺x嵗昗傪 丂丂丂併b丗併a偺斾偵撪暘丒奜暘 偡傞嵗昗偱偁傞丏 |
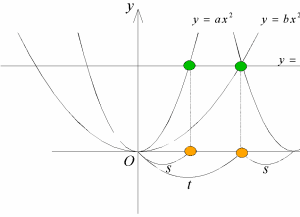 徹柧)
徹柧)
曻暔慄偐傜嫟捠愙慄傪堷偄偰丆愙揰偑捀揰偲側傞傛偆偵偡傞丏
偝傜偵丆捀揰偑尨揰偵偔傞傛偆偵暯峴堏摦偡傞偲丆曻暔慄偼
丂丂丂y亖ax2丆y亖bx2
偲側傞丏偙偺偲偒丆y嵗昗偑堦掕抣y亖d偲側傞偲偒偺偦傟偧傟偺x嵗昗偺憹暘偺斾偑媮傔傞x嵗昗偺斾偲側傞丏
y亖ax2丆y亖bx2偺x嵗昗偺憹暘傪x亖s丆x亖t偲偡傞丏
丂丂丂as2亖bt2亖d
傛傝丆
丂丂丂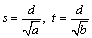
傛偭偰丆
丂丂丂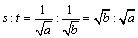
偱偁傞丏
丂偙傟傪棙梡偟偰嫟捠愙慄偺栤戣傪夝偄偰傒傛偆丏
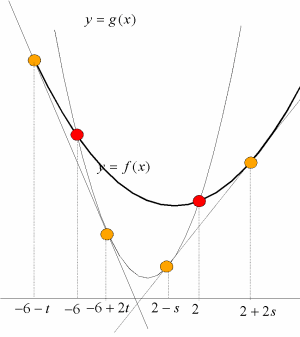
|
ex3)師偺俀偮偺曻暔慄偺嫟捠愙慄傪媮傔傛丏 丂丂丂f(x)亖4x2亄8x亅16丆g(x)亖x2亅4x亄20 |
夝)
偙偺俀偮偺曻暔慄偺岎揰偺x嵗昗偼丆
丂丂丂4x2亄8x亅16亖x2亅4x亄20
傛傝丆x2亄4x亅12亖0
丂丂丂(x亄6)(x亅2)亖0
丂丂丂亪丂x亖亅6丆2
偙偺x嵗昗偑俀愙揰傪1丗2偺斾偵撪暘偡傞揰偱偁傞丏
愙揰娫偺岎揰偺x嵗昗偑x亖2偺偲偒丆
俀愙揰偺x嵗昗偼丆x亖2亅s丆2亄2s偲偍偗傞丏
f'(2亅s)亖g'(2亄2s)傛傝丆8(2亅s)亄8亖2(2亄2s)亅4
偙傟傪夝偄偰丆s亖2
傛偭偰丆俀愙揰偺x嵗昗偼丆x亖0丆6傛傝丆
嫟捠愙慄偺曽掱幃偼丆y亖8x亅16
摨條偵丆岎揰偺x嵗昗偑x亖亅6偺偲偒丆
俀愙揰偺 嵗昗偼丆x亖亅6亅t丆亅6亄2t偲偍偗傞丏
f'(亅6亅t)亖g'(亅6亄2t)傛傝丆8(亅6亅t)亄8亖2(亅6亄2t)亅4
偙傟傪夝偄偰丆t亖亅2
傛偭偰丆俀愙揰偺x嵗昗偼丆x亖亅4丆亅10
嫟捠愙慄偺曽掱幃偼丆y亖亅24x亅80

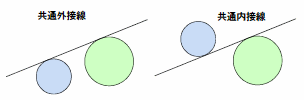 丂傂偲偮偺愙慄偵傛傝暯柺偼俀偮偺椞堟偵暘偗傜傟傞丏俀墌偑摨偠椞堟偵偁傝偦偺愙慄偵愙偟偰偄傞応崌丆偦偺愙慄傪嫟捠奜愙慄丆堎側傞椞堟偵俀墌偑偁偭偰愙偡傞応崌傪嫟捠撪愙慄偲偄偆丏
丂傂偲偮偺愙慄偵傛傝暯柺偼俀偮偺椞堟偵暘偗傜傟傞丏俀墌偑摨偠椞堟偵偁傝偦偺愙慄偵愙偟偰偄傞応崌丆偦偺愙慄傪嫟捠奜愙慄丆堎側傞椞堟偵俀墌偑偁偭偰愙偡傞応崌傪嫟捠撪愙慄偲偄偆丏
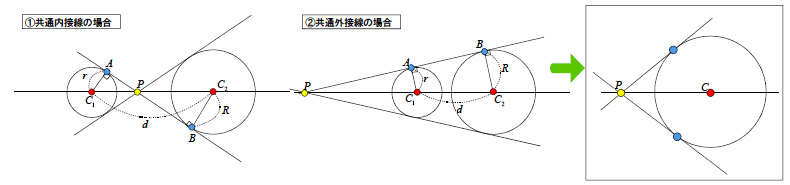
丂偙傟傜偺嫟捠愙慄偼丆俀墌偺敿宎r丆R(r亙R)偲俀墌偺拞怱C1丆C2偺嵗昗偐傜媮傔傞偙偲偑偱偒傞丏
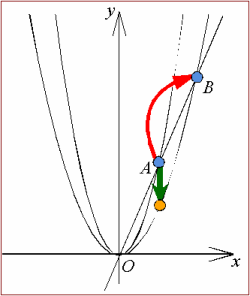
丂壓恾偺傛偆偵俀偮偺墌偺愙揰傪偦傟偧傟A丆B偲偟丆俀愙慄偺岎揰傪P偲偡傞丏
偙偙偱丆仮PAC1佷仮PBC2偱偁傞偐傜丆
丂丂丂PC1丗PC2亖r丗R
傛偭偰丆揰P偼丆慄暘C1C2傪r丗R偺斾偵暘偗傞揰(嫟捠奜愙慄偺応崌偼奜暘揰丆嫟捠撪愙慄偺応崌偼撪暘揰)偱偁傞丏偟偨偑偭偰丆偦偺嫟捠愙慄偼丆偙偺揰P偐傜丆俀墌偺偳偪傜偐堦曽傪慖傫偱丆偦偺墌偵堷偄偨愙慄傪媮傔傞栤戣(墌奜偐傜堷偄偨愙慄栤戣)偵婣拝偡傞偙偲偵側傞丏
| 俀偮偺墌偺敿宎傪r丆R丆拞怱傪C1丆C2偲偡傞丏 俀墌偺嫟捠撪愙慄(奜愙慄)偼丆慄暘C1C2傪r丗R偺斾偵撪暘(奜暘)偡傞揰偐傜丆俀墌偺偳偪傜偐偵堷偄偨愙慄偱偁傞丏 |
|
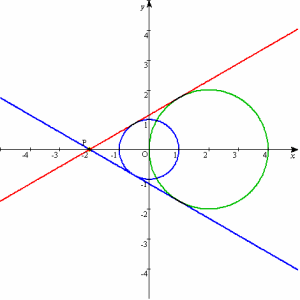
ex4)師偺俀偮偺墌偺嫟捠愙慄傪媮傔傛丏 丂丂丂x2亄y2亖1丆(x亅2)2亄y2亖4 |
夝)
俀墌偼岎傢傞偐傜媮傔傞愙慄偼俀杮偺嫟捠奜愙慄偱偁傞丏
俀墌偺敿宎偼偦傟偧傟1丆2傛傝丆拞怱C1(0丆0)丆C2(2丆0)傪1丗2偺斾偵奜暘偡傞揰P(亅2丆0)偐傜墌x2亄y2亖1偵堷偄偨愙慄傪媮傔傟偽傛偄丏
愙慄偼y幉偵暯峴偱偼側偄偐傜孹偒傪m偲偡傞偲丆y亖m(x亄2)丏
偙偺捈慄偲墌x2亄y2亖1偺拞怱C1(0丆0)偲偺嫍棧偑墌偺敿宎1偵摍偟偗傟偽傛偄偐傜丆
丂丂丂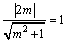
偙傟傪夝偄偰 丏
丂丂丂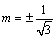
埲忋傛傝嫟捠愙慄偼丆
丂丂丂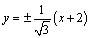
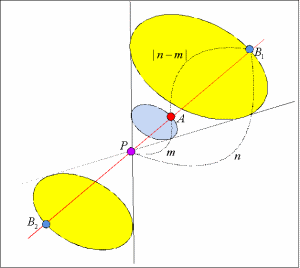 丂尨揰傪憡帡偺拞怱偲偟丆俀師嬋慄f(x丆y)亖0傪m丗n偺斾偵奼弅偟偨婳愓偺曽掱幃傪媮傔傞丏
丂尨揰傪憡帡偺拞怱偲偟丆俀師嬋慄f(x丆y)亖0傪m丗n偺斾偵奼弅偟偨婳愓偺曽掱幃傪媮傔傞丏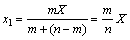
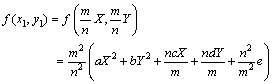
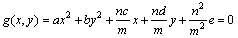
 丂b亖0丆d亗0偺偲偒丆俀師嬋慄偼幉偑y幉偵暯峴偱偁傞曻暔慄傪昞偡丏
丂b亖0丆d亗0偺偲偒丆俀師嬋慄偼幉偑y幉偵暯峴偱偁傞曻暔慄傪昞偡丏