

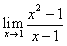
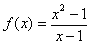 �̃O���t�ƁCg(x)=x+1�̃O���t�̈Ⴂ�͂Ȃ����낤�D
�̃O���t�ƁCg(x)=x+1�̃O���t�̈Ⴂ�͂Ȃ����낤�D���悵�����͂��Cx=1�Œ�`����Ă��邩�ǂ����̈Ⴂ�ł�����ˁD
���܂Ȃԁ��搶�́C�����Ă�����Ă����Ă���D
���܂Ȃԁ�������C
�@�@�@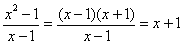
�ƕό`���邱�Ƃ́C�Ă錊�߂邽�߂̕ό`���Ƃ������Ă��D
����@���� �݂�Ȃ͒m�炸�m�炸�̂����ɁC���邱�ƂŃO���t�ɋĂ������߂Ă���킯���D
�@y=f(x)�́Cx=1�ŕs�A����(�Ƃ�������`����Ă��Ȃ�)��������Cx=1�ɋ߂Â����Ƃ͂ł��邯�ǁCx=1�̒l�͑��݂��Ȃ��D�Ⴆ��C�����Ă��铹�̓r���ɐ����肪����݂����Ȃ��̂��D���̐�����̐^���ɍs���ɂ́C�������y�Ŗ��߂Ă������킯�ŁC���߂�ꂽ�������̏ꍇ�Cx=1�ŘA���Ȋ�y=g(x)���Ă��ƂɂȂ�D���Ƃ́C�ړI�̏ꏊ�ɂ����Cg(1)�����߂�����D ���Ȃ킿
�@�@�@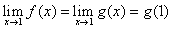
�ƂȂ�D
�@���̂悤�ɁC�������̋Ɍ������߂�ɂ́C���Ƃ��Ζɂ���đ�ւ̘A���Ȋ���p�ӂ�����@���l������D
�ł́C���̃O���t�̌����߂ɂ����@�����K�Ŋm�F���Ă݂悤���D
|
ex) ���̋Ɍ��l�����߂�D �@(1) 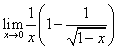 �@�@(2) �@�@(2) 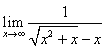 �@�@(3) �@�@(3) 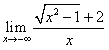
|
�������q�� �܂�(1)�ˁD������݂�ƁCx=0��x=1�̂Q���Ɍ����Ă��D
���悵�����ł��Cx��0������Cx=0�̌����߂�����Ώ\���D���̂��߂ɂ́C
�@�@�@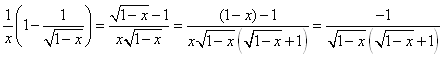
�@����Ō������܂����D�����āCx��0�Ƃ���C�����߂�������x=0�������Ă��ƁC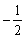 �ƂȂ�܂��D
�ƂȂ�܂��D
�������q���ł�(2)�ˁD�ł�����́C�ǂ��Ɍ����Ă���̂�����D��ʓI�ɂ͂��̎�̖��́C�u����̗L�����v�ł���ˁD
�@�@�@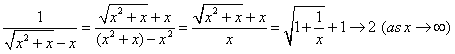
�@�݂����Ȃ��Ƃ��Ă邩��C����ς茊���߂Ȃ̂�����D
�@�搶�C�����̃e�[�}�Ƃ��̖��͍���Ȃ��̂ł͂Ȃ��ł��傤���D
���܂Ȃԁ����[��C�搶�̂��Ƃ����炫���Ɖ�����݂�����D�l���v���ɁC���Ԃ��̐�ɋĂ��錊�̌����߂��Ă��Ƃł͂Ȃ����낤���D
����@�������ς�炸�܂ȂԂ͔��z�����͉s���Ƃ����˂��Ă�ȁD���Ⴀ�C������Ƃ��̊��ɖ��@���|���Ă݂悤�D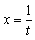 �Ƃ����Ă����D
�Ƃ����Ă����D
���܂Ȃԁ����̂ˁC�搶�D�K�L����Ȃ�����D�`�`���v�C�v�C�ł��Ȃ��ł��傤�D
�@���傤���Ȃ��D���Ⴀ�C������ƕt���������D
�@�@�@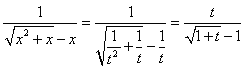
�ƂȂ�܂��D
����@�����ł́Cx�����Ƃ���ƁCt�͂ǂ�Ȓl�ɋ߂Â����낤���D
�������q��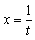 �ŕ��ꂪ�傫���Ȃ��Ă�������C�������Ct�����ł��ˁD
�ŕ��ꂪ�傫���Ȃ��Ă�������C�������Ct�����ł��ˁD
���悵�������m�ɂ����ƁCt��+0�ł���ˁD
����@���������C�E�Ɍ��ɂȂ�ˁD�����ŁC��قǂ̊���t��0�ɋ߂Â���Ɓc�c�C
�������q�������C���ꂪ0�ɂȂ�Dt=0�̂Ƃ���Ɍ�������D�����L�������āC�����߂��ł������ˁD
�@�@�@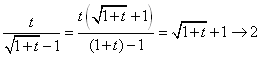
����@�����l�Ԃ͖����̐�͌��ʂ���قNJ�p�Ȑ������ł͂Ȃ��D������C�����ɍs�����Ƃ��Ă�����̂��茳�Ɉ����߂����Ƃɂ���Ē]�т�U���H�v����������D���ꂪ�C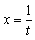 �Ƃ��������Ƃ������Ƃ��D������g����(3)�̖����������ʂ����悭�Ȃ�D
�Ƃ��������Ƃ������Ƃ��D������g����(3)�̖����������ʂ����悭�Ȃ�D
���܂Ȃԁ������ł����D�����̐搶�C������Ɨc�t���ۂ��ł���D(3)���Ċm���C�����v�Z�̈����|�����ł�����ˁD
�@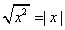 �ŁC���̏ꍇ�Cx���|��������Cx��0���C
�ŁC���̏ꍇ�Cx���|��������Cx��0���C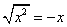 �ƂȂ邱�Ƃ𗘗p�����ł���D
�ƂȂ邱�Ƃ𗘗p�����ł���D
���悵�����܂ȂԁC�������Ȃ��Ő搶�͎����������Ď茳�Ɉ�������Ă����Ă���̂��Ǝv����D���̂��߂ɂ� ���ǂ��u�������邩���Ă��Ƃ��ˁD
�������q��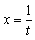 �ł���D�����u���ƁCx���|���ɂ���ƁCt��0�ƂȂ��D
�ł���D�����u���ƁCx���|���ɂ���ƁCt��0�ƂȂ��D
���܂Ȃԁ��܂Ă�C�����q�D�ł����̏ꍇ�̋߂Â����́Cx��0������Ct��-0�ƂȂ��Ă���ς��قǂ̐�Βl�̖�肪�c���Ă����D
�������q�������ˁC�m���ɍ����Ƃ̗��݂ň����ɂ�����ˁC���Ƃ���Ɓc�c�C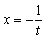 �ˁC���������t��+0�ƂȂ��D
�ˁC���������t��+0�ƂȂ��D
����@�����������C���ꂶ��C�v�Z���Ă����D
�������q���͂��C����Ă݂܂��D
�@�@�@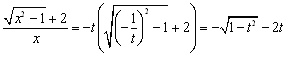
�@������Dt=0�̌������܂�����D���Ƃ́Ct��+0�Ƃ���ƁC����-1�Ɏ��������D
����@���������ԁC�����߂�����Ă����ˁD����ł͂��悢�捡���̖{�肾�D
|
ex2) ���̓��������藧�悤�ɁC�萔a�Cb�̒l���߂�D �@(1) 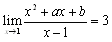 �@(2) 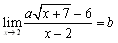 �@(3) 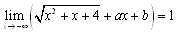
|
���܂Ȃԁ������D�������̖��ŏI��肶��Ȃ������́C��������D���[���ƁC���x�́C�Ɍ��l�͂����������Ă����ł��ˁD
����@���������C�����猊�����܂�悤�ɁCa�Cb�����߁C�����߂�Ƃ������Ƃ��D
���悵�����m���C(����)��0 �Ȃ�C(���q)��0 �ƂȂ邱�Ƃ𗘗p���������ˁD
����@�����������C���̕��@�͋Ɍ�����܂��Ă���ꍇ�ɂ����g���Ȃ����璍�ӂ��悤�D
�@�@�@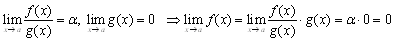
�Ƃ������Ƃ��D
�@�ł͖��������Ă݂Ȃ����D
���悵����(1)�ł����C����́C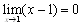 ������C
������C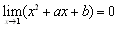 �ł��D
�ł��D
�@�@�@��1+a+b=0
���ꂩ��C
�@�@�@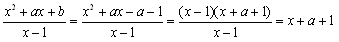
�@����ŁC�������܂������ɂȂ�܂����D
�@����āC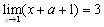 ������C
������C
�@�@�@a=1�Ab=-2
�������܂��D�܂�����a,b�ɑ��ċt�����炩�ɐ������Ă��܂��D
���܂Ȃԁ��ł��ȂC�������邢�ȁD���̂悤�ɍl������ǂ����낤���D
�@���̏ꍇ�̕��q��x2+ax+b�Ȃ�Q�����ł��邱�Ƃ͊m�肵�Ă�킯������C
�@�@�@(���q)=(x-1)(x+c)
�ƒu���Ă��܂��ƁC
�@�@�@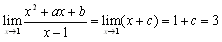
�@���ꂩ�炩��c=2
�@����āCx2+ax+b=(x-1)(x+2)=x2+x-2
�ƂȂ邩��C�W�����r���āCa=1�Ab=-2�D�ǂ����낤�D
�������q���Ȃ�قǂˁD�������C���̂����̌����C�܂ȂԂˁD
���܂Ȃԁ�����������́C����ȂɌ�������Ȃ��ȁD�ł�(2)�͂����͂��܂������Ȃ���ȁD
�������q�����Ⴀ�C��������Ă������D
�@����̋Ɍ��́C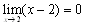 ������C
������C 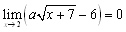
�@���ꂩ��C3a-6=0�@��a=2�@����āC
�@�@�@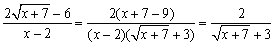
�@����ŁC�����ߊ����D����x��2�Ƃ���ƁC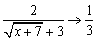
�@�ȏ���C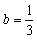 �ƂȂ�܂��D
�ƂȂ�܂��D
����@�����ł́C���悢�惉�X�g�̖�肾�D�ǂ�����D
���悵�����搶�̍D���Ȏ����ł���ˁD0�Ɏ�������悤�ɂ��邽�߂ɁC
�@�@�@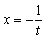 �Ƃ����ƁCx��-���̂Ƃ��Ct��+0
�Ƃ����ƁCx��-���̂Ƃ��Ct��+0
�ƂȂ�܂��D�����������ƁC
�@�@�@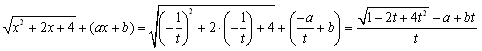
�������q�������āC���̌�͕��q�̗L�����ł���ˁD
���܂Ȃԁ����傢�܂��C�����q�C���̂����͑ʖڂ���D
�@�@�@(����)��0�@����D������C(���q)��0
�@����g����ł���C�搶�C�����ʼnA���ȃg���b�v�ŁC�l�����������|���悤�Ƃ����ł���D
�������q������ˁC�ł��C�Ȃ�قǁD���ꂪ���܂�ɊȒP�Ȏ������猩�����Ă��܂�����D����Ō����߂�����킯���D
�@�@�@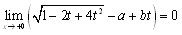
�@����āC1-a=0�@��a=1
�@���̂Ƃ��C
�@�@�@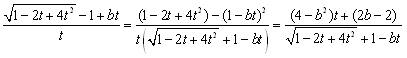
�@�ǂ��ɂ��C�����߂ł��܂����D�Ō�ɁCt��+0�Ƃ���ƁC
�@�@�@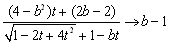
�@�����ŁC�Ɍ��l��1�ł����������C
�@�@�@b-1=1
�@���@b=2�ƂȂ�܂��D
����@�����悭�ł����ˁD���́C�Ō�̖��̉́C�����q���������悤�ȕ��@�ł͂Ȃ��C�����P���ɖ����̐���݂邱�Ƃň�ʂɂ͋��߂�D�ł��ق�̂�����Ƃ܂��Ȃ��������Ă��ƁC�����̐悪�r�[�C�����̎茳�Ɉ������Ă��܂��D�����ɗ���Ă������݂���ԋ߂������݂ɂȂ��Ă����肷��D�������C����͋t�������邱�ƂɂȂ�D�߂������݂��Ǝv���Ă��Ă��C������Ƃ������t�ʼn������݂ɂȂ��Ă��܂����Ƃ�����D
�@���ӂ��Ȃ��Ⴂ���Ȃ���ȁD�܂ȂԁD
���܂Ȃԁ��Ō�̌��t�C������ƈӖ��[����Ȃ��D�Ђ���Ƃ�����C�搶�C�ƒ�ł��܂������ĂȂ���Ȃ��́D
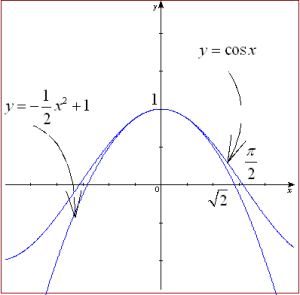
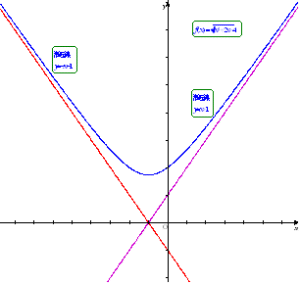 ex2��(3)�́C�Ȑ�y=f(x)�����̖������_�ł͂ǂ�Ȓ����ɋ߂Â��Ă������Ƃ����悤�ɂ݂邱�Ƃ��ł��܂��D���Ȃ킿�C���߂钼���́C
ex2��(3)�́C�Ȑ�y=f(x)�����̖������_�ł͂ǂ�Ȓ����ɋ߂Â��Ă������Ƃ����悤�ɂ݂邱�Ƃ��ł��܂��D���Ȃ킿�C���߂钼���́C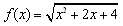 �̑Q�ߐ��Ɖ��߂ł��܂��D
�̑Q�ߐ��Ɖ��߂ł��܂��D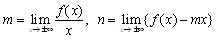
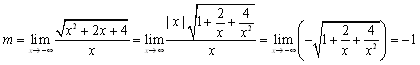
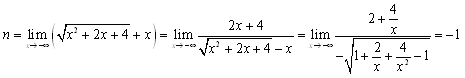
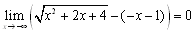
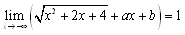
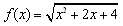 �̑Q�ߐ����l���邱�Ƃ��ł���̂́Cf(x)�̎����͂P���Ƃ݂Ȃ��邱�Ƃ��C�Ȑ��͖�����order�����ʂł��钼���ɋߎ��ł��邩��ł��D���������āC���̖��̉́C�{���ł��q�ׂĂ���悤�ɁC���̂悤�ɖ������order���r���ċ��߂邱�Ƃ��ł��܂��D
�̑Q�ߐ����l���邱�Ƃ��ł���̂́Cf(x)�̎����͂P���Ƃ݂Ȃ��邱�Ƃ��C�Ȑ��͖�����order�����ʂł��钼���ɋߎ��ł��邩��ł��D���������āC���̖��̉́C�{���ł��q�ׂĂ���悤�ɁC���̂悤�ɖ������order���r���ċ��߂邱�Ƃ��ł��܂��D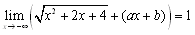 ���C
���C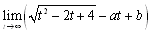
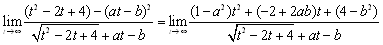 �@�@�c�c(��)
�@�@�c�c(��)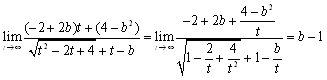
�@x2����x3�̕���������ɂȂ�X�s�[�h���������߂ɏ�̉�(��)�̔�r���ł��܂��D���̂悤�ɁC�����̐�̊��̑傫�����r����ɂ́C�������order(����)�𗘗p���܂��D
| 0���������̂Ƃ��C�@log x��x����x����ex�@�ix�����j |
�@f(x)��g(x)�ł���Ƃ��Cg(x)��f(x)��荂�ʂ̖�����ƂȂ�܂��D���ꂩ��
�@�@ 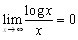
�@�A 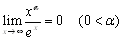
����������͖̂��炩�ł��D��q�̖��̉��C0����������x����x���𗘗p�������ƂɂȂ�܂��D
�@�������C����ex2)(3)�̉́Ca�Cb�̕����̔��f����n�܂�C���ɕ��q�E�����order���r������ƁC���낢����������C�Ō�ɂ́C�Ō�ɂ͂��������
�@�@�@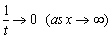
�Ƃ��C0�Ɉ����ċɌ������߂Ă��܂��܂��D�����Ƃ����B���͌ЂȂ��̂֔���Ă��܂����C��Ԑg�߂�0�ɋ߂Â��������̕]������������������₷���Ȃ�͓̂�����O�̂��Ƃł��傤�D
�@�����ŁC���̖�������order�ɂ��Ĉȉ��C�����G��Ă݂܂��傤�D
�@�Ⴆ�C
�@�B 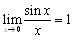
�@����́C0�̋ߖT�ł�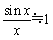 �@���Ȃ킿sin x��x�ł���C��y=sin x�̃O���t�����_�̋߂��ňꎟ�̒���y=x�ɋߎ��ł��邱�Ƃ�\���Ă��܂��D�܂��Cf(x)=sin x�Ƃ���C
�@���Ȃ킿sin x��x�ł���C��y=sin x�̃O���t�����_�̋߂��ňꎟ�̒���y=x�ɋߎ��ł��邱�Ƃ�\���Ă��܂��D�܂��Cf(x)=sin x�Ƃ���C
�@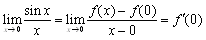
�ł�����C����y=x�́Cy=f(x)�̐ڐ��ł���C���͐ړ_�̋ߖT�ł͐ڐ��ŋߎ��ł���Ƃ���������O�̂��Ƃ������Ă��܂��D
�s�b�x��t
�@���������āC�B����x=0�ł̔����W����\���Ă���ƍl�����܂��D�Ƃ��낪�Csin x�̓��������߂邽�߂ɂ́C�B�̋Ɍ��𗘗p���܂�����C�����W���Ƃ݂Ȃ����Ƃ͏z�_�@�Ƃ��Ƃ�܂��D�������B�̋Ɍ������߂邽�߂ɂ͉~�̖ʐϔ�r�����܂����C���̉~�̖ʐς����߂邽�߂ɁC���ڑ��p�`�̖ʐς̋Ɍ������߁C�����ɂ܂��B�̋Ɍ����g���܂��D���������Ă�����܂��z�_�@�ƂȂ�܂��D���ǂ��̂ւ�̂Ƃ���͐[����͂��Ȃ��ق��������悤�ł��D
�@���āC���l�ɁC
�@�C 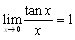
�́Cx��0�̂Ƃ��Ctan x��x�ł���Cy=tan x��x=0�̋ߖT�ł͒���y=x�ɋߎ��ł��邱�Ƃ������܂��D
�@�D 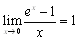
�@������Cx��0�Ŏw����y=ex���Cy=x+1(������ڐ�)�Ɉꎟ�ߎ��ł��邱�Ƃ��Ӗ����܂��D���̂��Ƃ̓l�C�s�A���̒l�ɂ��ւ���Ă��܂��Dy=ex�̃O���t�������ɂ́C�܂��Ȑ���x=0��̓_�i0�C1�j(y�ؕ�)�ɂ�����X���P�̐ڐ��������C���̏�Ɏw�������悹�܂����C
�@�@�@y�ؕЂ̐ڐ��̌X�����P�ɂȂ�Ƃ��̎w����y=ax�̒�a�̒l��a=e
�ł���Ƃ��������C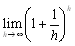 �̋Ɍ��ׂ�������o�I�ɂ�������₷���Ƃ����܂��D
�̋Ɍ��ׂ�������o�I�ɂ�������₷���Ƃ����܂��D
 �@�܂��Cf(x)=ex�̋t�����l����Cy=log x�ɂ��ẮC
�@�܂��Cf(x)=ex�̋t�����l����Cy=log x�ɂ��ẮC
�@�E 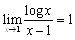
�ł���C�����x��������-1���s�ړ����邱�ƂŁC
�@�F 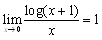
�������܂��D���̂悤��x=0�ł̂P���ߎ��́C���ʂƂ��Ċ��̐ڐ���\���܂��D������y=cos x�ɂ��ẮCx=0�ł̐ڐ���y=1�ł�����C
�@�G 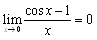
�ƂȂ葼�Ƃ��̒l���قɂ��܂�(���ʂ̖������ł͂Ȃ�)�D
�@�����ŁC�]�����̏ꍇ�́C�����ł͂Ȃ��C�Ȑ�(������)�ɂQ���ߎ������邱�Ƃ��l���܂��Dx=0�̋߂��ł̊T�`��������ɑΉ������C����y�ؕЁC�O���t�̊J�����v�������ׂ�Ηe�Ղ�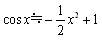 �̊W���\�z����C���̋Ɍ��������܂��D
�̊W���\�z����C���̋Ɍ��������܂��D
�@�H 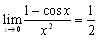
�@�Ƃ���ŁC���̂悤�Ȑ����̋ߎ��́C�����̒藝���C���ϒl�̒藝�CTaylor�W�J�C����ɂ�Maclaurin�W�J�ւƊg�����邱�ƂŎ�����܂��D
|
�sMaclaurin�W�J�t ��f(x)��0���܂ފJ��Ԃ�n������\(Cn����)�ł���C �@�@�@ 
|
�@�����ŁC��]��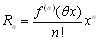 �́Cf(x)�Ƃ̌덷���Ӗ����܂����C
�́Cf(x)�Ƃ̌덷���Ӗ����܂����C
�@�@�@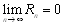
�ł���C��f(x)�́CMaclaurin�����̘a
�@�@�@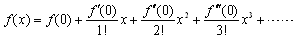
�Ƃ��ĕ\���܂��D�����K���ȂƂ���Ő�o���Cf(x)��x�̑������Ƃ��ċߎ����邱�Ƃ��ł��܂��D
�@���Ƃ��Cf(x)=cos x�́C
�@�@�@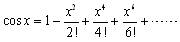
�ƓW�J�ł��܂����C�Q���܂Ő�o�������̂��C�I���ł���킯�ł��D
�@��������������܂��D
�@�@�@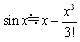
�@�@�@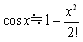
�@�@�@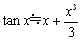
�@�@�@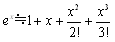
�@�@�@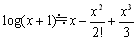
�@����𗘗p����C�Ɍ��l���e�ՂɌ��ʂ���悤�ɂȂ�܂��D
|
ex) ���̋Ɍ������߂�D �@(1) 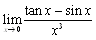 �@�@(2) �@�@(2) 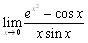 �@�@(3) �@�@(3) 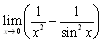
|
�\�z)
�@(1) 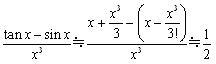
�@(2) 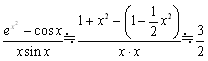
�@(3) 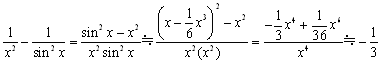
�@�s��`�̋Ɍ������߂�ɂ́C�@��i�Ƃ��ă��s�^���̒藝������܂��D�������C���s�^���̒藝���Ŏg�����Ƃɂ͕S�Ƒ��̂���Ƃ���ł���C�ւ���Ƃ��Ă����w�������ɂ����Ă��܂��D���̃��s�^���̒藝�������Ă��Ă���̂R����������Ƃ͓���ł��傤�D
�@�����āC�������̂��Ə�q�̂悤�ȉ́CMaclaurin�W�J�ł̌덷�̕]�������Ă���킯�ł�����C�܂����������Ę_�O�Ƃ����܂��D�ߎ��ɂ���@�œ���ꂽ�Ɍ��͌��ł͂Ȃ����Ǘ\�z�ɉ߂��Ȃ��̂ł��D
�@�����ŁC���̋ߎ��̍l���������������^�����C���߂邱�Ƃ��ł���悤�ɂ��邽�߂ɁC��������order�����Ă݂܂��傤�D
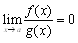 �̂Ƃ��Cf(x)��g(x)�ɔ�ׂč��ʂ̖�����(order������)�Ƃ����C �̂Ƃ��Cf(x)��g(x)�ɔ�ׂč��ʂ̖�����(order������)�Ƃ����C�@�@�@f(x)=o(g(x))�@�ix��a�j �ƕ\�� |
�@���Ȃ킿�Cf(x)�̕���g(x)��薳�����ɂȂ�X�s�[�h�������Ƃ������Ƃł��D
�@���̖������̏���(order)��\���L��o�������_�E�̃I�[�Ƃ����܂��D(E.Landau)
�Ⴆ�C
�@�@�@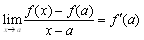
�ł�����Corder�ŕ\���ƁC
�@�@�@f(x)-f(a)-(x-a)f'(a)=o(x-a) �@�ix��a�j
�ƂȂ�܂��D
�@�Ƃ���ŁC�����ŁC���̎��̓����́C���ӂ̊����E�ӂ̎��ŕ]������Ƃ������Ƃł���C��ʂ̓����̐����͕K��������������킯�ł͂���܂���D�Ⴆ�C
�@�@�@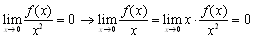
�ł�����Co(x2)=o(x)�ƂȂ�܂����C�t��o(x)=o(x2)���K�������������Ȃ����Ƃ͖��炩�ł��傤�D
�@���̃����_�E�̃I�[�̐����̑�\�I�Ȃ��̂��C�܂Ƃ߂Ă����܂��D
|
x��0�ł���C �@(1) xmo(xn)=o(xm+n) �@ (2) o(xm)o(xn)=o(xm+n) (3) m��n��o(xm)+o(xn)=o(xm) |
�@(1)��
�@�@�@f(x)=o(xn)�Ƃ����ƁC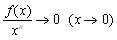
�@����āC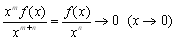
�@�@�@���@xmf(x)=o(xm+n)
(2),(3)�ɂ��Ă����l�ɁC�e�ՂɎ�����܂��D
����(3)�́C
�@�@�@m=n�̂Ƃ� o(xm)+o(xm)=o(xm)
�ƂȂ�܂��D
�������_�E�̃I�[�Ɋւ���̏ڂ������Ƃ́C�@����order���g���ƁC(Maclaurin)�W�J�͎��ɂ悤�ɕ\���ł��܂��D
�@�@�@�u��������ϕ��v�O��q�P�� (�|����)
�@�@�@�u�Q�ߓW�J�Ɋւ��郁���v�@��t�F��(���s�{���G�H���Z)
��������������
|
f(x)�� ���܂ފJ��Ԃɂ����āC�����\�ł���Ȃ�C �@�@�@ 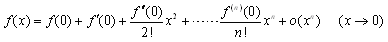
|
�ؖ�)
�@�@�@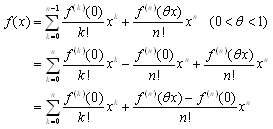
�@�����ŁCf(x)�͔����\���x=0�ŘA���ł��邩��C
�@�@�@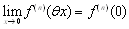
�@����āC 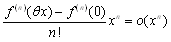
�@���̂悤��order�ɂ��Maclaurin�W�J���C�Q�ߓW�J�Ƃ����܂��D
�@�����đQ�ߓW�J���g�����ƂŊ��̋Ɍ��́C�B���ł����������̕�������������ċɌ�����������Ƌ��߂��܂��D
�@�O�q��ex�Ŋm�F���Ă݂܂��傤�D
�@���Q�ߓW�J�ɂ�����
�@(1) 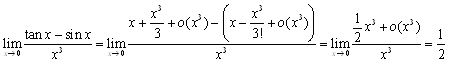
�@(2) ex=1+x+o(x)���Cex2=1+x2+o(x2)
�@����āC
�@�@�@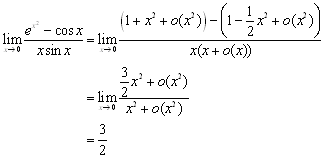
�@(3) sin x���P���܂œW�J���āCsin x=x+o(x)
�@3���܂œW�J���āC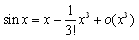
�@���ꂩ��C
�@�@�@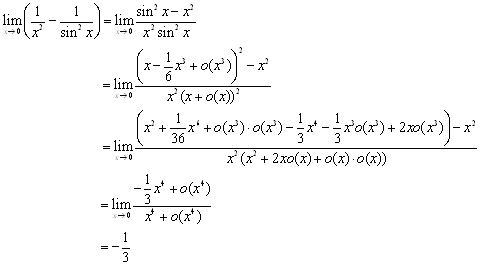
�ǂ̖����C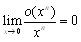 �ł��邱�Ƃ𗝉����Ă����C�P���ȓW�J�v�Z�ŋɌ����^�����܂��D
�ł��邱�Ƃ𗝉����Ă����C�P���ȓW�J�v�Z�ŋɌ����^�����܂��D
�@�������C���̕��@�́CMaclaurin�W�J�ɂ������]�������̌덷���C�������Ă���킯�ł͂���܂��C��l��0�Ɏ��������邱�ƂŋɌ������߂Ă��܂��D�ߎ��l�̌덷�]���͂ł��Ȃ��̂ł��D �܂��C�����̍��܂őQ�ߓW�J������������Ƃ������Ƃ��C����Ȃ��ƌ˘f����������܂���D
�@���̂悤�ɁCMaclaurin�W�J�CMaclaurin�����ł̋ߎ��C���s�^���̒藝�C�����ă����_�E�̃I�[�ɂ��Q�ߓW�J�C��������������ׂ�A�C�e���ł����C�K�X�C�A�C�e���������Ďg�p��������킯�ł��D
�@������ɂ��Ă��C������̔���ɔ�ׂāC�ڂɌ�����(�{���͌����Ȃ��̂ł���)�������C�������̕��������ƈ����₷���Ƃ�����̂ł��D
�@�Ƃ���ŁC�{�����̂܂ȂԂƂ����q�ł����C����C�u���̂����v�Ƃ����L�[���[�h�œ�l�̊W�ɏ����Ђт���������������܂���D���t�̑������ɂ���Ă͎���ۂ������Ԃ�ς����̂ł��D���炵���Ȃ��܂ȂԂƁC���Ȃł��邩���q���C���[�W����u���̂����v�Ƃ������t�͂��ꂱ���C�������Ɩ�����قǂ̊J��������̂�������܂���D
�@�g���܂݂ō��N�x�̖����オ��܂����D