

札幌新川高等学校 中村文則
○なかをとって<先 生>二次関数の最大点・最小点は,定義域が与えられている場合,
区間の両端におけるグラフ上の点,頂点
のいずれかになることを学んだんだよな。それでは,問題だ。
| ex) 次の最大値,最小値を求めよ。 (1)y=x2-4x+3 (0≦x≦5) |
<まなぶ>はい,標準形に変形して,
y=(x-2)2-1
これから,軸の方程式は,x=2ですからグラフが下に凸の放物線になり,頂点が最小点より,最小値はx=2のとき,y=-1です。
<先 生>では,次に最大値だ,かず子。
<かず子>軸と区間の両端までの距離を考えると,x=5の方が離れているから,最大値は,x=5のとき,y=8です。
<先 生>OK!,これは楽勝だね。では次,(2),よしお,今度はどうかな。
<よしお>標準形に直します。
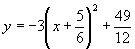
したがって,上に凸の放物線ですから,頂点で最大になります。最大値は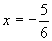 のとき,
のとき,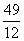 です。
です。
最小値は,軸と区間の両端との距離のより離れている方だから,えーっと……。
<先 生>まなぶ,手助けだ。計算してごらん。
<まなぶ>エッ!,はい。
左端との距離は,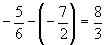
右端との距離は,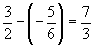
だから,左端の方が離れているから,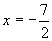 で最小となります。
で最小となります。
<先 生>まっ,後は頑張って計算すりゃいいわけだ。ところでだ。区間の両端と軸との距離でどちらがより離れているかもう少し簡単に判断する方法はないだろうか。
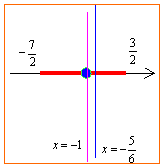
<まなぶ>両端のy座標の値を直接求めては…。
<先 生>それも,ひとつの手だね。どうせ最大値を求めるわけだからy座標は必要だしね。でも,やっぱり片方の値は無駄になる。他に方法はないだろうか。
<生 徒>………
<先 生>よし,ではヒント。区間の中点のx座標は何だろうか。
<よしお>両端の値を足して2で割って,x=-1です。
<かず子>あっ,そうか,中点の座標と軸を比較すればいいんだ。
<先 生>その通り。軸に対して中点が左右どちらにあるか見ればいいんだ。今の場合,軸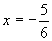 の左側に中点x=-1があるから左端で最小値をとることが分かる。何事も,中庸が肝心ということだよ。
の左側に中点x=-1があるから左端で最小値をとることが分かる。何事も,中庸が肝心ということだよ。
○七・五・三へのモデル化
<先 生>今日は放物線の最大・最小の応用問題に挑戦だ。
| ex) 次の最大値,最小値を求めよ。 f(x)=x2-4x+1 (a≦x≦a+1) |
<よしお>はい,f(x)=(x-2)2-3です。だから,軸の方程式はx=2,頂点の座標は(2,-3)です。
<先 生>では,次に区間だが,いままでと違ってこの問題の場合はaの値によって区間が変化するからちょっと扱い難いね。だけど,区間の幅は,
(a+1)-a=1
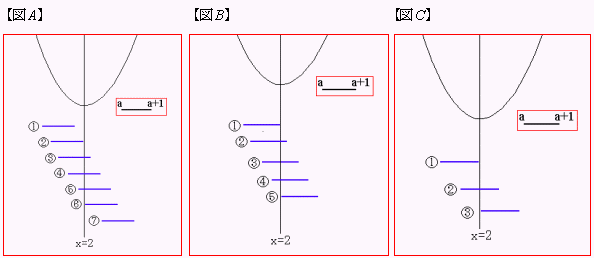
と常に変わらないことに注意しよう。さて,この区間をx軸に沿って左から右に変化させ,両端および頂点での値の変化を考えながら,最大点,最小点の変わり目となる区間を調べてみよう……(黒板で区間を変化させ実際に確認)
図1のように7つの場合に分けられることが分かるね。でもちょっと多すぎるからもう少し整理してみよう。
この中で,①は区間の左端が最大点で,右端が最小点の場合だけど,②は左端が最大点に対して,最小点は右端であると同時に頂点とみることもできる。すなわち,②は最小点の場所が右端から頂点に変化する「変わり目」なんだ。同じように考えれば,⑥は最大点が頂点から左端へと変化する変わり目とみることができるだろう。この変わり目を基準に分けると図Bのように5つのケースを考えればいいことが分かる。
では,他に変わり目はないだろうか。調べてごらん。
<かず子>先生,③も最大点の変わり目だと思います。
<先 生>確認してみよう。②は左端,③はグラフの対称性から左端と右端どちらも最大点だ,④は右端。
うん,確かにそうだね。この変わり目で分けてやれば,最終的に図Cのように3つのケースで考えれば充分ということになる。
さて,次にこの3つのケースのそれぞれの変わり目におけるaの値を求めてみよう。例えば①は,右端が軸x=2にくっ付いているから,
a+1=2 よってa=1
というように求めればいい。同様にして,③のときのaの値はなんだろう,まなぶ。
<まなぶ>はい,左端が軸にくっ付いてるからa=2です。
<先 生>では②の場合はどうだろう,かず子。
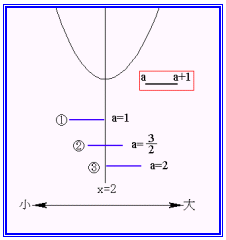 <かず子>はい,区間の中点を求めると,
<かず子>はい,区間の中点を求めると,
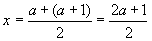
中点は軸x=2の上にあることから,
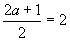
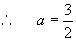
です。
<先 生>その通りだね。でもね,区間が連続的に変化しているんだから,②は当然①,③のaの値の平均でなければいけないよね。だから,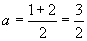 と考えた方が簡単なんだ。
と考えた方が簡単なんだ。
次に,aの値の変化を確認してみよう。①~③へと変化するとき,aの値はだんだん大きくなっているね。これを図のように描いてやる。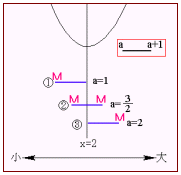 さあ,これで,モデル図の完成だ。
さあ,これで,モデル図の完成だ。
このモデル図を利用して最大値,最小値を求めていこう。
まず,①~③の最大値をとる場所を図のようにMで表してみる。最大点は,
①左端 ⇒ ②左端,右端 ⇒ ③右端
と変化し,その変わり目は②であることが分かる。このとき,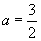 であるから,このaの前後で場合分けをすればいいんだ。よって,最大値は,
であるから,このaの前後で場合分けをすればいいんだ。よって,最大値は,
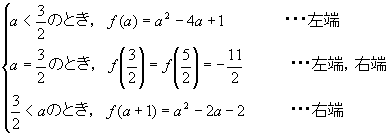
では,同様に最小値を考えてみよう。よしお,やってごらん。
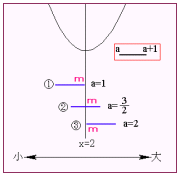 <よしお>まず,最小点をとる場所をmで表します。
<よしお>まず,最小点をとる場所をmで表します。
①右端,頂点 ⇒ ②頂点 ⇒ ③頂点,左端
と変化するから,①と③が変わり目となります。a=1とa=2で分けて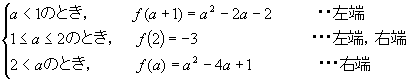
<先 生>では,応用問題。
| ex) 次の関数の最大値・最小値を求めよ。 f(x)=-x2+ax+1 (1≦x≦3) |
 今度は,グラフがaの値によって変化する場合だ。どうすればいいだろう。
今度は,グラフがaの値によって変化する場合だ。どうすればいいだろう。<かず子>先ほどの問題と同じように,グラフを変化させて場合分けします。
まず,2次関数を標準形に変形して,
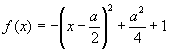
ですから,軸の方程式が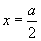 ,頂点
,頂点 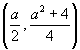 である上に凸の放物線となります。
である上に凸の放物線となります。
次に,区間に対して,グラフを左から右に向かって移動させ,図のように3つのケースに分ければいいと思います。
<先 生>そうだね。でも,このモデル図は先ほどの区間が変化する場合の問題と比較するとちょっと,分かり難いよね。実はもっとシンプルにモデル化できるんだ。
まなぶ,ちょっと前にでてきてごらん。(先生は,黒板に長めの区間を描いてから)さあ,まなぶ,君は放物線だ。黒板に書いた区間に対して左から右に向かってちょっと歩いてごらん。
(まなぶは言われたように移動する)
みんな,いいかな。今,まなぶに実際にこの問題のグラフの動きを再現して貰ったんだ。ところで,まなぶ,君にとって黒板に書いてある区間はどのように変化していただろう。
<まなぶ>……
<先 生>もう一度動いて自分の目の動きを考えてご覧。
(まなぶは言われた通りに動く)
<まなぶ>あっ,区間がだんだん左に遠ざかっていきます。だから区間は,右から左に向かって動いてます。
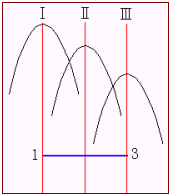
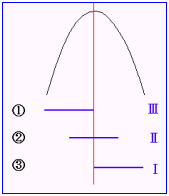 <先 生>その通りだ。みんなもまなぶの立場で考えてごらん。区間と放物線の関係は実は相対的なものなんだ。普段はみんなは固定された区間を基準に放物線の変化を考えるけど,放物線上に眼をおいて眺めると,今度は区間が動いているように見える。例えば,自動車に乗って風景を眺めている様子を考えてごらん。右手前方に建物があるとしたら,その建物は後方に流れていくね。でも実際は車が前方に向かって走っている訳だ。そう考えると,次の図を見てごらん。先ほど,かず子が示した図は,
<先 生>その通りだ。みんなもまなぶの立場で考えてごらん。区間と放物線の関係は実は相対的なものなんだ。普段はみんなは固定された区間を基準に放物線の変化を考えるけど,放物線上に眼をおいて眺めると,今度は区間が動いているように見える。例えば,自動車に乗って風景を眺めている様子を考えてごらん。右手前方に建物があるとしたら,その建物は後方に流れていくね。でも実際は車が前方に向かって走っている訳だ。そう考えると,次の図を見てごらん。先ほど,かず子が示した図は,
①⇔Ⅲ ②⇔Ⅱ ③⇔Ⅰ
と対応していることが分かるはずだ。結局この問題の場合も,区間が変化する場合と同様に考えていいということなんだ。
では,この図を使ってモデル図を完成させよう。よしお,①~③の場合のaの値を求めてみよう。
<よしお>①ですが,右端のx=3が軸にくっついているから,
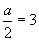 ∴ a=6
∴ a=6
同様に③は,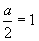 ∴ a=2 ②は①と③の平均をとって,
∴ a=2 ②は①と③の平均をとって,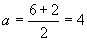 です。
です。
<先 生>では,次にaの変化だ。まなぶ。
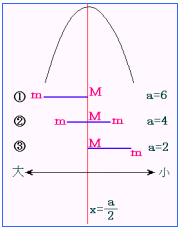 <まなぶ>区間が右にあるほどaの値は小さくなってます。
<まなぶ>区間が右にあるほどaの値は小さくなってます。
<先 生>では,最後に最大点をM,最小点をmとして図に書き入れていこう………ようし,これで完成だ。さあ,答えを書いていこう。まずは最小値。よしお,変わり目は。
<よしお> ①左端⇒②左端,右端⇒③右端と変化してますから,変わり目は②のaの値です。だから,a=4です。
<先 生>正解!,従って,a<4,a=4,4<aで場合分けをすればいいのだけれど,ここで大事なことは,aの増減の変化だ。先ほど区間が右にいくほどaの値は小さくなっていることを確認したね。さあ,かず子,まとめてごらん。
<かず子>
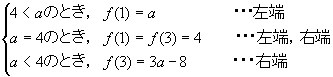
となります。
<先 生>最大値も,同じように考えると,
①右端,頂点⇒②頂点⇒③頂点,左端 より,変わり目は①と③であることから,次のような解答が得られる。
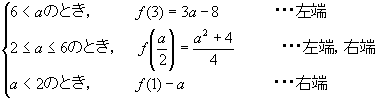
さあ,本時のまとめだ。②の変わり目のaを求めるには,区間の中点を求めるのではなく,①と③のaの値の平均を求めた。グラフが変化する問題も,グラフ上からみれば区間の変化となる。
発想を転換してちょっと視線を変えてみると,違った世界がみえてくるものなんです。