

| ex) x=2で極小値3,x=2で極大値5をとる3次関数f(x)を求めよ。 |
<まなぶ>わーっ、僕の大嫌いな問題だ。
これって、f(x)=ax3+bx2+cx+dとおいて、単純に計算していくやつですよね。パス。
<かず子>しょうがないわね。私がやってあげるわ。
f'(x)=3ax2+2bx+c
ここで、x=2,4で極値をとるから、f'(2)=0,f'(4)=0
よって、 12a+4b+c=0 ……①
48a+8b+c=0 ……②
また、f(2)=3,f(4)=5であるから、
8a+4b+2c+d=3 ……③
64a+16b+4c+d=5 ……④
あとは、①~④の連立方程式を解けばいいのよね。うーん、確かにやりたくないわね。
<よしお>僕が計算するよ。……でました。a=-1/2,b=9/2,c=-12,d=13です。先生,でもこれで終わりじゃないのですよね。
<先 生>そう、f(x)=-1/2x3+9/2x2-12x+13となるけど、これが条件を満たすしているかどうか調べなきゃならない。
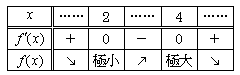 <かず子>f'(x)=0は、接線の傾きが0ということでしかないということでしたよね。X=2,4のそれぞれで、極大・極小となっていることを確認します。
<かず子>f'(x)=0は、接線の傾きが0ということでしかないということでしたよね。X=2,4のそれぞれで、極大・極小となっていることを確認します。
f'(x)=-3/2x2+9x-12=-3/2(x-2)(x-4)
より、右の増減表から条件を満たしていることが分ります。
<まなぶ>どうやらできたけど、でも、やっぱりこの問題、しっくりこないなあ。
<かず子>どんな点が。
<まなぶ>だってね。3次関数の概形って以前先生が教えてくれたよね。変曲点を考えればその点に関して点対称であることよりグラフが簡単にかつ綺麗に描けるって。さらに、最高次の係数をみればグラフの増減も予想できるわけだから、増減表を書くのだって無駄なことやってるような気がするんだ。
<かず子>でも、本音は変数が4つもある連立方程式を解くのが面倒くさいんでしょ。
<先 生>変数が4つといっても1次の方程式だから、それほど面倒なことではない。でも、実は変数の個数を減らし、増減表も書かなくていい方法があるんだ。
<まなぶ>なんだ、先生。それなら最初からその方法で説明してよね。
<先 生>そんなことしたらただでさえ計算が苦手なまなぶは、完全に計算音痴になってしまうだろ。
<かず子>いえてる。
<先 生>その方法のポイントは、プレビューだ。
<よしお>巻き戻しということですか。
<先 生>そう、いままでも何度か使った方法だね。みんなが先ほどやった解答は、3次関数を微分して極値となる点を調べ、増減表を書いて、確認したわけだ。それを増減表から予測してしまうんだ。
具体的に示そう。題意のように、x=2で極小値,x=4で極大値をとるように増減表がかけるためには、f'(x)はどういう形になっていればいいだろう。
<かず子>f'(x)=0の解が、x=2,x=4だから、……f'(x)=a(x-2)(x-4)ですか。
 <先 生>その通り。でもその形では、x=2で極小、x=4で極大となることまで示されていない。定数aの符号はどうであればいいだろう。
<先 生>その通り。でもその形では、x=2で極小、x=4で極大となることまで示されていない。定数aの符号はどうであればいいだろう。
<よしお> 極小点が極大点の右にあるから、a<0ですね。
<先 生>したがって、x=2で極大、x=4で極小になるには
f'(x)=a(x-2)(x-4) (a<0)
であればいいということをいっておく。これで、増減表を書く必要はなくなる。
<まなぶ>なるほど、プレビューという意味が分りました。そうすると、さらにこれを微分する前に戻してf(x)を求めればいいんですね。
<先 生>正解だ。では、f(x)はどうなるだろう。
<かず子>えーっと、f'(x)=a(x2-6x+8)だから、微分してx2になるのは次数を一つ高くしてx3。でもx3を微分すると係数が3になって、……、分りました。
F(x)=a(1/3x3-3x2+8x)
です。まなぶ、いいでしょ。
<まなぶ>凄い、4つだった変数が、たった1つになっちゃった。
<先 生>本当にそうだろうか。
<よしお>まてよ、かず子、定数って微分すると0だろ。そうすると、いまかず子が求めた式に適当な定数をくっつけておいても導関数は一緒じゃないだろうか。
<先 生>よしおのいう通りだ。すなわち、
f(x)=a(1/3x3-3x2+8x)+b
とおけるということだ。
<まなぶ>なんだ。変数が2つに増えちゃった。
<かず子>それでもずいぶん計算が楽になったわ。
あとは、f(2)=3,f(4)=5から式を作ればいいだけだわ。まなぶ、やってごらんよ。
<まなぶ>だって、代入すると、分数の計算がでてくるじゃないか。パス!
<かず子>もーっ、ぐうたらなんだから。私がやるわ。代入して、
20a/3+b=3,16a/3+b=5
これを解いて、a=-3/2,b=13
よって、
f(x)=-3/2(1/3x3-3x2+8x)+13=-1/2x3+9/2x2-12x+13
となるわ。
<まなぶ>まあ、確かに少しは楽になったみたいだな。
<かず子>なんか、まなぶはまだ不満そうみたいね。
<先 生>ぐーたらまなぶに合わしたくはないけど、それじゃあ、もう少し簡単に求めることを考えてみようか。
<まなぶ>なあんだ、先生あるじゃない。出し惜しみして。
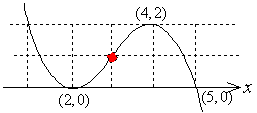
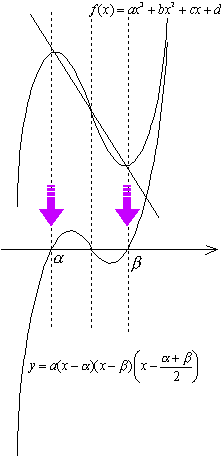
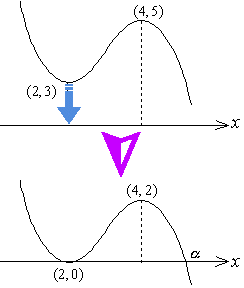 <先 生>(……まなぶを無視して……)、まず、問題文の情報から、求める三次関数の概形を予想して書いてごらん。
<先 生>(……まなぶを無視して……)、まず、問題文の情報から、求める三次関数の概形を予想して書いてごらん。
<よしお>さきほど の符号を調べたときに予想したように、右図のような形ですよね。
<先 生>では、次にグラフを下に下降させて、極小点が 軸にぶつかるまで、落としてごらん。
<かず子>はい、図のようになります。
<先 生>ではみんなに聞くけど、こうやって落としたグラフの方程式はどう表されるだろう。
<よしお>極小点でx軸と接するんですよね。ということは(x-2)2の形になりますよね。
<かず子>さらに、もう一箇所 軸と交わる点があるから、その交点のx座標をx=αとすると、(x-α)も因数に持つわ。
そうすると、ひょっとしたら
y=(x-2)2(x-α)
ですか。
<先 生>惜しい。肝心なものを忘れている。グラフの開きぐあ……
<まなぶ>分った。Y=a(x-2)2(x-α)でしょ。
<先 生>鳶に油揚げをさらわれたような気分だ。その通り。さあ、そうすると元の式は今度はそれを下げた分だけ上げていけばいいだろう。
<かず子> f(x)=a(x-2)2(x-α)+3ということですよね。でも先生。αの値が分らないんじゃこの先進めませんよ。
<先 生>そのαの値、本当に分らないだろうか。
<まなぶ>意味深ですね。なんか験されているようで癪に障るな。
<先 生>三次関数のグラフの性質をもう一度よーく思い出してごらん。
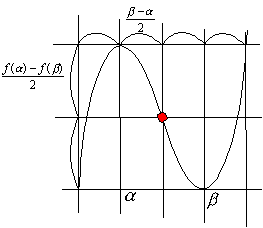 <まなぶ>あっ、分ったぞ。8個の長方形でしょう。
<まなぶ>あっ、分ったぞ。8個の長方形でしょう。
<かず子>そうか。変曲点や極点を基準に8個に分けた合同な長方形の中に三次関数が綺麗に納まってしまうって性質ね。
<よしお>右図のことですね。
<先 生>そう、その通り。ではいまの場合のグラフについて8つに切ってみよう。一つの長方形の横の長さはどれだけだろう。
<かず子>極点のx座標の差は2だから、長方形の横の長さは1です。
<まなぶ>そうすると、残りのx軸との交点は、x=5ですね。
すなわち、
f(x)=a(x-2)2(x-5)+3
ということですね。
すごい。1つの変数でf(x)が表現できちゃった
<かず子>ほんと。凄いわ。4つあった変数がたった1つになっちゃうのね。
 <先 生>さあ、ではあとはこのaの値を求めて終わりだ。どうする。
<先 生>さあ、ではあとはこのaの値を求めて終わりだ。どうする。
<よしお>曲線上の点を代入すればいいと思います。極大点はf(x)を作るときに使ってないからこの点を代入します。
<まなぶ>じゃ今度は僕が計算してあげよう。
F(4)=5 だから、
F(4)=a×3×(-1)+3=5
これから、a=-1/2
∴ f(x)=-1/2(x-2)2(x-5)+3
となるね。
あとは、これを展開して整理すれば終わりだ。
<先 生>いつものように最後の美味しいところをまなぶが掻っさらっていってしまった。でも、ルーズなまなぶ的思考も、考えてみると数学ではとても重要なことではないだろうか。よく洒落て「数楽」って読んで、「数学は楽しむ」ものだとこじつけちゃうけど、「数楽」は、「数学を楽する」とも読める。いかに計算も含めて楽になるか追及していく過程で、発想や公式といったものが生まれてくるのではないだろうか。
<まなぶ>何か、こそばゆいな。じゃあ、先生、もう少しお言葉に甘えていいですか。いっそのこと変数を全部なくすることはできないのですか。
<先 生>前言を撤回する。
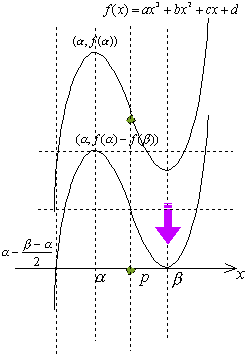 3次関数f(x)=ax3+bx2+cx+dの極大点、極小点をそれぞれ(α,f(α)),(β,f(β))とします。すなわち、a>0とします。このとき、変曲点は、
3次関数f(x)=ax3+bx2+cx+dの極大点、極小点をそれぞれ(α,f(α)),(β,f(β))とします。すなわち、a>0とします。このとき、変曲点は、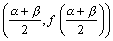
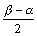 となりますから、残り 軸との交点の 座標は、
となりますから、残り 軸との交点の 座標は、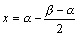 となることより、
となることより、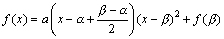
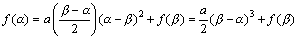
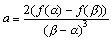
 グラフには、その式の表現法として、一般形、標準形、切片形といった形が通常用意されています。
グラフには、その式の表現法として、一般形、標準形、切片形といった形が通常用意されています。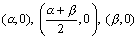
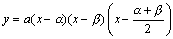
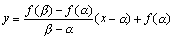
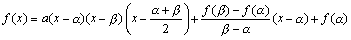
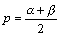 ですから、
ですから、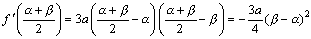
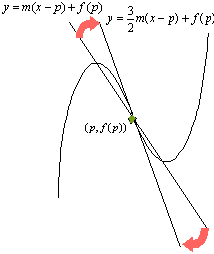 ここで、
ここで、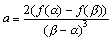
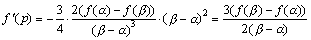
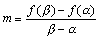
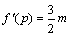
| 変曲点における接線の傾きは、2極点を結ぶ直線の傾きの3/2倍である |
という結論が得られます。
また、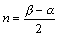 とすると、
とすると、
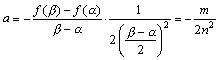
これから、
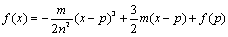
となることが分ります。
| ex) 3次関数f(x)がx=1で極小値2,x=3で極大値6をとるとき、関数f(x)を求めよ。 |
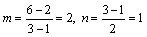
f(x)=ax3+bx2+cx+dの2極点のx座標をα,βとすると、
f'(x)=3a(x-α)(x-β)
となりますから、
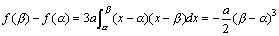
これからαの値を簡単に求めることができます。
また、3次関数の標準形は、変曲点を中心として考えられることは次のことからも分ります。
3次関数をx=pを極として、taylor展開すると、
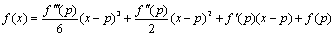
となりますが、x=pが変曲点のx座標であれば、f"(p)=0より、
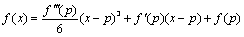
よって、3次関数の標準形が得られました。