数列のプロポーズ方法

＜先　生＞次の問題を見てみよう。

＜まなぶ＞はい、等差数列と等比数列の積で各項が作られているからです。

＜先　生＞そうだったね。それでこの数列をmarriage数列なんて命名したけれど、では、この和はどうやって求めたんだろう。

＜かずこ＞等差と等比の積ですけれど、数列の性質としてより強い影響を与えているのは、等比数列ですから、その和の求め方を利用しました。

＜先　生＞等差数列は、等比数列にくっ付いている係数(ゴミ)みたいなものだといったね。そこで、等比数列のもともとの和の求め方に帰着させて、和をSとしたときに、その両辺に公比に相当する２をかけて与式から辺々引いてやるわけだ。

　さて、そこで今日の授業のテーマだけど、違ったアプローチでこのmarriage数列の和を求めてみよう。

　よしお、ところで、階差数列って何だっけ。

＜よしお＞数列の隣り合う二項の差をとって作られる数列のことです。

＜先　生＞黒板(右図)のように階差をとっていくと、

　　a₁+b₁+b₂+……+b_n-1=a_n………(＊)

　という関係式が得られるんだったね。

　実は、この階差を利用すると、marriage数列の和を求めることができるんだ。

　では、marriage数列の階差数列を計算してごらん。

＜まなぶ＞各項の差をとって

　　　3，8，20， ………

　先生、何かわけの分からない数列になっちゃいますけど。

＜先　生＞それは、階差の取り方が悪いからだよ。marriage数列の一般項は、a_n=n・2^k-1　ということはすでに分かっているわけだから、b_n=a_n+1-a_nを計算すれば、階差数列｛b_n｝の一般項が得られるだろ。

＜まなぶ＞あっ、そうか。

　　　b_n=(n+1)・2ⁿ-n・2^n-1=(n+2)・2^n-1

となります。

＜先　生＞そうだね。それではみんな、ちょっと黒板をみていてごらん。このあとは先生が説明していこう。

　数列｛a_n｝とその階差数列との関係(＊)から、

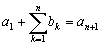
　よって、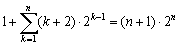　
　　　　　　

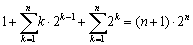
　ここで、　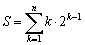だから、

　　　1+S+2(2ⁿ-1)=(n+1)・2ⁿ

　以上より、S=(n-1)・2ⁿ+1

　さあ、なぜか不思議と和が求められてしまったね。数列の結婚までのアプローチは、当世、ワンパターンじゃ嫌われてしまうもんなんです。キラリと光る個性をちょっと覗かせる演出を忘れちゃいけないよな。

Ｎｏｔｅ）

　「不思議と和が求められる」と本文はまとめていますが、実際は不思議でもなんでもありません。marriage数列が等比数列の性質を色濃く反映していることを考えれば、その求和法から自然に導かれるものなのです。

　等比数列の和Sは、

　　　S=a+ar+ar²+……+ar^n-1

に対して公比rを両辺にかけてその差をとれば求められますが、実は

各項に公比をかけるということは、項をひとつずらすということを意味し、
その差をとるということは、階差をとることを意味する

　実際、等比数列｛a_n｝

　　　a，ar，ar²，ar³，ar⁴，……，ar^n-2，ar^n-1，arⁿ

の初項から第(n+1)項までの階差をとると、

　　　(r-1)a，(r-1)ar，(r-1)ar²，(r-1)ar³，(r-1)ar⁴，……，a(r-1)r^n-2，(r-1)ar^n-1

なる階差数列が得られることから

　　　a+(r-1)(a+ar+ar²+……+ar^n-1)=arⁿ

　これから、等比数列の和の公式が導き出されます。

　このように考えると、数列の単元の指導法の組立てとして、次のような配置を考えても面白いかもしれません。

　なお、本文は、この指導の組立ての流れで創作したものです。