

○ 努力は報われる話
| <先 生> | 今日は,2次方程式 x2+(1+i)x+(−2−i)=0 の実数解を求めてみよう。どうすればいいかな。
|
| <生徒C> | 因数分解できないから,解の公式を使うと思いますが。
|
| <先 生> | (はまった…)。では,解の公式に当てはめてごらん。
|
| <生徒C> | 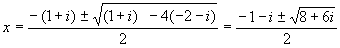 , あれ? , あれ?
|
| <先 生> | 分かったかい。一般に解の公式は有理数係数の2次方程式でしか使えないんだ。でもせっかくここまで計算したから,続きを考えてみよう。問題は,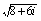 の計算ができるかということなんだけど,どうだろうか。 の計算ができるかということなんだけど,どうだろうか。
|
| <生徒達> | ………
|
| <先 生> | では,ちょっとヒントをだそう。複素数を図形的に捉えると,どんな意味をもっていたかな。
|
| <生徒B> | えーと,相似変換と回転変換でした。あっ,そうか。
とみれば,計算できます。
|
| <先 生> |
そうだね。では,Aさん,続きをやって。
|
| <生徒A> |
 z=8+6iとおけば,
z=8+6iとおけば,
となります。
これから,
|
| <先 生> | さあ,あとは,三角関数の半角の公式をちょこっと使えば完成だ。
よって, 以上より,2次方程式の解は,
これから,2次方程式の解の公式は,どうやら複素数係数の場合でも使えそうみたいですね。だけどね。もう一度よく,問題をみてごらん。最初に要求していた解はなんだったのかな。
|
| <生徒A> | あっ,実数解です。
|
| <先 生> | そう,だから虚数の解まで求める必要はないんだ。実は,この手の問題は一般には次のように解答すればいい。 実数解をx=αとし,方程式に代入しよう。 α2+(1+i)α+(−2−i)=0 実部と虚部に分けて, (α2+α−2)+(α−1)i=0 これから,α2+α−2=0,α−1=0 であるから,α=1 ∴ 実数解はx=1。
|
| <先 生> | 随分,計算が簡単になってしまったね。問題をよく読まないとさっきみたいな回り道をすることになるんだ。 さあ,それでは,最後の質問だ。では,この2次方程式の虚数解と実数解を求めるにはどうすればいいだろうか。
|
| <生徒達> | (不思議そうに),エッ?
|
| <生徒A> | 先生,それをさっき解の公式で求めたのではないですか。
|
| <先 生> | 先生のいった質問の意味を考えてごらん。虚数解と実数解といったね。複素数解を求めろということではないよ。
|
| <生徒達> | ……
|
| <先 生> | では,ヒント。2次方程式問題で,三種の神器といえば,なんだったろう,B君。
|
| <生徒B> | 「解の公式」,「判別式」,それと「解と係数の関係」。あっ,ひょっとすると解と係数の関係ですか。
|
| <先 生> | その通り。解の公式が複素数係数の2次方程式で使えるのなら,解と係数の関係だって使えるよね。ちょっとやってごらん。
|
| <生徒達> | 2次方程式の2解をα,βとすると, α+β=−1−i,αβ=−2−i となります。
|
| <先 生> | ここで,αを実数とみると,2式より,
β=(−α−1)−i, 2式を比較して,α=1,β=−2−i が得られる。 さあ,今日のまとめだ。最初は解の公式で解いて随分回り道をしたけれど,結局,そのお陰で複素数係数でも解と係数の関係が使えそうなことが分かったね。生徒が苦労して,徒労に終わるというけど,最初の苦労は無駄ではなかったということです。苦労は報われるものなのです。
|
<付 記>
複素数係数の2次方程式 ax2+bx+c=0 も解の公式で求めることができます。
方程式を (x−α)2=z と平方完成すると,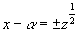
 極形式に変形して,
極形式に変形して, 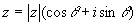
これから,
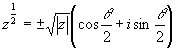
ここで,半角の公式より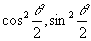 の値が求められますが,
の値が求められますが,
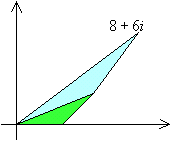
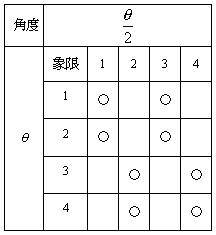
θと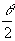 の象限の関係に注意し(右図参照)
の象限の関係に注意し(右図参照)
![]() の値の1つをαとすると,
の値の1つをαとすると,
x=α±β
が得られます。