

○ものぐさの勧め
<先 生>(a+b)nの展開式は,
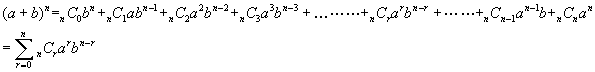
となり,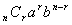 を一般項というんだったね。今日はこの一般項を利用して,展開式における各項の係数(二項係数)の値を求めてみよう。
を一般項というんだったね。今日はこの一般項を利用して,展開式における各項の係数(二項係数)の値を求めてみよう。
|
ex) 次の各式の展開式における,括弧内の項の係数を求めよ。 (1) (2x2-3)6 (x6) (2) (3x4-2x2)5 (x14) (3) 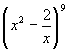 (定数項) (定数項)
|
<先 生>(1)の問題からだ。まず,一般項を求め整理してみよう,まなぶ。
<まなぶ> 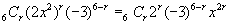 となります。
となります。
<先 生>OK!。従って,x6の係数は,2r=6よりr=3のときだから,二項係数は,
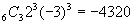
となる。では,次に(2)だ。かず子,同様に一般項を求めて整理してごらん。
<かず子>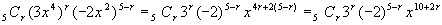
となります。
<先 生>では二項係数はどうなる,よしお
<よしお>10+2r=14よりr=2ですから,
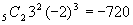
です。
<先 生>指数の部分の計算が結構,大変だね。次の(3)は分数式になるから,きっと,もっと大変なんだ。誰かやってくれる人いるかな?……いない!,しょうがない,では先生が一般項を求めてみよう。
(黒板に向かって忙しそうに計算を始める,格闘しているというイメージを生徒に与える演出を忘れずに)
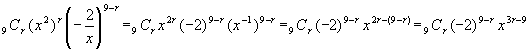
(生徒の方に向き直るが,ネクタイをちょっと緩めてまげておけば効果的)
<先 生>ふーっ!疲れた。(ここで額の汗を拭う)。さあ,この後はみんなにやってもらおう。定数項の値を求めるのだから,rの値は何だろう,かず子。
<かず子>はい,項x0の係数とみなせばいいですから,3r-9=0より,r=3となります。
<先 生>さあ,最後の計算だ,まなぶ。
<まなぶ> 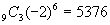 です。
です。
<先 生>さて,これで一応は解けたけど,(2)も(3)も指数の計算の部分が随分煩わしかったね。この部分をもう少しスリムに計算することはできないのだろうか。先生のようにものぐさな人間はこう考えてしまう。数学なんて学問は,大体が,ものぐさな人間がラクをするために作ったようなものだからね。では,具体的にどうするかということだけど,アイデアは簡単なんだ。
例えば,(2)の式は,まず次のように変形する。
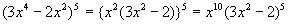
そうすると,この展開式におけるx14の係数は,x10を括り出してあるのだから,(3x2-2)5の係数から判断できることが分かるかな。どの項の係数を求めればいいことになるだろう,まなぶ。
<まなぶ>10と足して14になればいいのだから,x4の項の係数です。
<先 生>そうだね。あとは,(1)と同様に,(3x2-2)5の一般項を求めて,
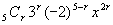
より,r=2の場合を計算して答えが得られる。どうだろう。随分あっさりとでてしまうね。
では,(3)はどうすればいいだろう,よしお。
<よしお>えーと,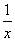 で括ればいいと思います。だから,通分して,
で括ればいいと思います。だから,通分して,
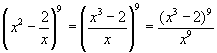
<先 生>その通り。従って,定数項を求めるには,何を考えればいい。
<よしお>はい,(x3-2)9の展開式のx9の係数です。一般項は,
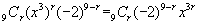
ですからね3r=9よりr=3
よって,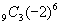 。ほんとだ,随分ラクですね。
。ほんとだ,随分ラクですね。
<先 生>いいかな。ものぐさに努めるための努力は惜しんじゃいけないんだよ。
Note)
ものぐさに努める一例として,本レポートを作りましたが,その背景にはもっと込み入った事情もあります。それは,現教育課程の「現地調達」的指導の調達法に関することです。コアとオプションを柔軟に配置し,系統的に単元を組み立てることが可能な教育課程は,現場実践主義に立つものですが,指導の組み立ての方向性がずれると論点が希薄になる危険性もあると感じています。
数列の単元もその一つです。等比数列を扱う上では指数法則の指導が不可避となります。大方は自然数の範囲で事足りますが,二項係数の問題に関しては,整数範囲での指数法則の理解が要求されます。もちろん数列の指導が指数・対数の単元の後に取り扱われれば何も問題はないのですが,学校事情によっては,数列を前にもってくることも実際あり得えるでしょう。(数列は数Aの単元,指数は数Ⅱの単元ですから,こちらの方が課程上,自然な流れではあります。(3)のケースは授業で取り扱わないと割り切ってしまえば,何も問題はないわけですが)。
ではそのときに現地調達で指数を取り入れればといっても,指数の分野は調達するには重すぎるように思います。この分野の一部分を切り取って指導してしまうと,二項係数の問題が指数の背面に隠れてしまい,混乱を引き起こしかねないのです。
現教育課程は,主幹のコアに対して枝葉のオプションを補うのが原則ですから,オプション分野にコアを調達のは馴染めないし,無理があるのでしょう。そのために本レポートのような工夫を通して,さり気なく,ものぐさにエッセンスだけを提供することも必要かと思うのです。