

嶥杫怴愳崅摍妛峑丂拞懞暥懃
| ex) 師偺俁揰傪捠傞曻暔慄偺曽掱幃傪媮傔傛丅 丂(1) A(3丆0)丆B(2丆0)丆C(0丆6) 丂(2) A(1丆3)丆B(3丆3)丆C(4丆9) 丂(3) A(亅1丆35)丆B(2丆5)丆C(5丆11) |
丂傑偢偼(1)傪夝偄偰偛傜傫丅
亙傑側傇亜傏偔偼偙偺3揰捠夁偺栤戣偼寵偄側傫偩傛側丅偨偩曻暔慄偺堦斒宍偵3揰傪戙擖偡傞偩偗偩傠丅側傫偐柺搢偔偝偔偰丅
亙偐偢巕亜側偵偄偭偰傫偺丅(1)偺栤戣偼丄3揰偲偄偭偰傕摿暿側揰偠傖側偄偺丅
亙傑側傇亜偊偭丄偁偭丄偦偆偐丅幉偲偺岎揰偩丅偦偆偡傞偲堦斒宍偠傖側偔偰丄壗偰偄偭偨偭偗丅僙僢僾儞乧乧丅
亙偐偢巕亜偄傗乕偹丄愗曅宍傛丅x幉偲偺岎揰傪(兛,0),(兝,0)偲偡傞偲丄曻暔慄偼y=a(x-兛)(x-兝)偲昞偝傟傞傢丅
亙傛偟偍亜偩偐傜丄偙偺応崌偼丄y=a(x-3)(x-2)丅 偙偙偱丄揰C傪戙擖偟偰僌儔僼偺奐偒a傪媮傔傞偲丄a=1
丂埲忋傛傝丄y=(x-3)(x-2)
亙偐偢巕亜偮偓偼丄(2)偹丅偙傟偼傑側傇偑偄偆傛偆偵扨弮偵戙擖偡傞偟偐側偄傢偹丅
亙愭丂惗亜偦偆偩傠偆偐丅偙偺栤戣偺3揰傕偦偺抣偵拲堄偟偰偛傜傫丅
亙傑側傇亜側偵偐偁傞傫偱偐丅偢偄傇傫3偑暲傫偱傞偺偼暘偐傞偗偳乧乧丅
亙傛偟偍亜偦偆偐丅A偲B偺y嵗昗偑摨偠偲偄偆偙偲偱偡偹丅
亙傑側傇亜偳偆偄偆偙偲偩偄丅
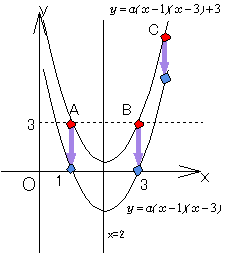 亙傛偟偍亜曻暔慄偺懳徧惈傪峫偊傟偽偄偄傫偩丅揰A偲揰B偺崅偝偑摨偠偲偄偆偙偲偼丄偦偺2揰偺拞揰偼幉忋偵偁傞偲偄偆偙偲偩傠丅
亙傛偟偍亜曻暔慄偺懳徧惈傪峫偊傟偽偄偄傫偩丅揰A偲揰B偺崅偝偑摨偠偲偄偆偙偲偼丄偦偺2揰偺拞揰偼幉忋偵偁傞偲偄偆偙偲偩傠丅
亙傑側傇亜偦偆偐丅偡傞偲幉偺曽掱幃偼倶亖2偩偐傜丄曻暔慄偼y=a(x-2)2+q偲偍偗傞偐傜丄偁偲偼揰傪戙擖偟偰a,q傪媮傔傟偽偄偄傫偩丅
亙愭丂惗亜偦偆偩偹丅偱傕丄傕偭偲暿側尒曽傪偡傞偙偲傕偱偒傞丅3揰偺倷嵗昗偐傜3傪堷偄偰偛傜傫丅
亙偐偢巕亜3揰偼丄(1丆0)丆(3丆0)丆(4丆6)偲側傝傑偡偹丅偁偭丄偙傟(1)偲摨偠偩傢丅
亙愭丂惗亜偙傟偼恾宍揑偵偼偳偆峫偊傟偽偄偄偺偐側丅
亙偐偢巕亜僌儔僼傪y幉曽岦偵亅3暯峴堏摦偝偣偰丄愗曅宍偵偟偨偲偄偆偙偲偱偡偹丅偩偐傜丄y=a(x-1)(x-3) 偵揰(4丆6)傪戙擖偟偰丄a=2丅偟偨偑偭偰丄y=2(x-1)(x-3)丅偦偟偰嵟屻偵傑偨y幉曽岦偵3暯峴堏摦偝偣傞偲丄y=2(x-1)(x-3)+3=2x2-8x+6偲側傝傑偡丅
亙愭丂惗亜偦偺捠傝偩丅偨偩偙偺応崌偼婎弨傪愗曅宍偐傜巒傔偨曽偑妝偩丅(1丆0)丆(3丆0)傪捠傞曻暔慄傪y幉曽岦偵3暯峴堏摦偟偨傕偺偲傒偰傗傟偽丄媮傔傞曽掱幃偼丄y=a(x-1)(x-3)+3偲偍偗傞丅偁偲偼揰B(4丆9)傪戙擖偡傟偽偄偄丅偱偼嵟屻偼(3)偩偹丅
亙傛偟偍亜偙傟偼傕偆偳偆偟傚偆傕側偄偱偡偹丅堦斒宍y=ax2+bx+c偵戙擖偟偰丄乧乧丅
亙傑側傇亜傛偟偍丄傑偰傛丅杔偼懠偺曽朄偑偁傞偲巚偆側丅
亙傛偟偍亜偳偆偟偰偩偄丅
亙傑側傇亜偩偭偰丄(1),(2)偺栤戣傪傒偰傒傠傛丅愗曅宍偱夝偄偰偄傞偩傠丅愭惗偺偟偮偙偄惈奿傪峫偊傞偲(3)偩偗偑偨偩戙擖偡傞側傫偰壗偐銬偵棊偪側偄傛丅栤戣偺揰偩偭偰傢偞偲寁嶼偑柺搢側傛偆側悢抣偵偟偰偄傞偟丅
亙愭丂惗亜偁傑傝榑棟揑側悇棟偲偼偄偊側偄偑丄娫堘偭偰偼偄側偄丅幚偼崱擔偺杮摉偺僥乕儅偼3揰捠夁偺曻暔慄傪愗曅宍偱夝偄偰傒傛偆偲偄偆偙偲側傫偩丅
亙傛偟偍亜愭惗丄偙偺3揰偼側偵偐摿庩側揰側傫偱偡偐丅
亙愭丂惗亜偄傗丄愭惗偑丄揔摉偵偲偭偨揰偩傛丅
亙傛偟偍亜偦傟偱偼偳傫側3揰偑梌偊傜傟偰傕愗曅宍偱曽掱幃偑媮傔傜傟傞偭偰偙偲偱偡偹丅
亙愭丂惗亜偦偆丄偦傟傕幚偵娙扨偵偱偒傞傫偩丅
亙偐偢巕亜偱傕丄(2)偲堘偭偰崅偝偑堘偭偰偄傞傢偗偩偐傜丄擄偟偄傛偆側婥偑偡傞傫偱偡偗偳丅
亙傑側傇亜偩偐傜丄崅偝傪摨偠偵側傞傛偆偵偡傟偽偄偄偭偰偙偲側傫偩傠偆偗偳丄暘偐傜側偄側偁丅
亙愭丂惗亜僸儞僩傪偁偘傛偆丅3揰偺偆偪2揰丄偦偆偩側B偲C偵偟傛偆偐丄偙偺2揰傪捠傞捈慄偺曽掱幃傪傑偢媮傔傛偆丅
亙傑側傇亜孹偒偼丄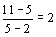 偩偐傜丄y=2(x-2)+5=2x+1
偩偐傜丄y=2(x-2)+5=2x+1
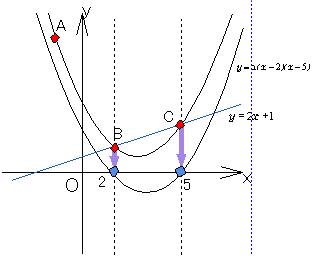 亙愭丂惗亜師偵3揰傪捠傞曻暔慄傪揔摉偵梊憐偟偰昤偒丄媮傔偨捈慄BC傪堷偄偰偛傜傫丅愗曅宍偑尒偊偰偙側偄偐偄丅
亙愭丂惗亜師偵3揰傪捠傞曻暔慄傪揔摉偵梊憐偟偰昤偒丄媮傔偨捈慄BC傪堷偄偰偛傜傫丅愗曅宍偑尒偊偰偙側偄偐偄丅
亙傛偟偍亜妋偐偵丄曻暔慄偵傛偭偰捈慄偑愗傜傟偰偄傞傢偗偩偐傜偙偺晹暘傪愗曅偲傒傟側偄偙偲偼側偄偗偳孹偄偰偄傞偐傜傑偢偄偱偡傛偹丅
亙偐偢巕亜偦傟偠傖偁丄捈慄偲x幉偲偺岎揰傪拞怱偲偟偰曻暔慄忋偺2揰B丆C偑x幉忋偵偔傞傑偱夞揮偝偣偨傜偳偆偐偟傜丅
亙傛偟偍亜偆乕傫丄偱傕偦傟偩偲x嵗昗偺抣傕曄傢偭偰偟傑偆偟丄偦傟傪媮傔傞偺傕戝曄偩傛丅戞堦幉偑y幉偲暯峴偱側偔側偭偰偟傑偆丅偱偒傟偽x嵗昗偺抣傪曄偊側偄偱丄愗曅宍傪嶌傟傟偽嵟崅側傫偩偗偳丅
亙傑側傇亜傒傫側丄壗偦傫側偵擄偟偔峫偊偰偄傞傫偩偄丅娙扨偩傠丅曻暔慄偺曽掱幃偐傜2x+1傪堷偗偽偄偄偩傠丅傎傜丄偙偆傗偭偰丄曻暔慄忋偺奺揰偐傜2x+1偺抣暘偩偗堷偄偰揰傪僾儘僢僩偡傞偲愗曅宍偑晜偐傫偱偔傞偩傠丅
亙偐偢巕亜杮摉偩傢丅偱傕丄傕偲傕偲偺曻暔慄偑暘偐偭偰偄側偄偺偩偐傜堷偒傛偆偑側偄偲巚偆偗偳丅
亙傛偟偍亜偄傗丄戝忎晇偩傛丅(2)傪夝偔偲偒偵愭惗偑偄偭偰偨傠丅傕偲偺曻暔慄傪婎弨偵偡傞傫偠傖側偔偰丄愗曅宍傪婎弨偵偟偨曽偑峫偊傗偡偄偭偰丅偩偐傜丄愗曅宍偵2x+1偺抣傪壛偊偨傕偺偑丄傕偲偺曻暔慄偲傒側偣偽偄偄傫偩丅
亙愭丂惗亜寢榑偑偱偨偹丅傑側傇偺偄偆偲偍傝偩丅媮傔傞曻暔慄偐傜2x+1暘倷嵗昗偺抣傪堷偄偰傗傞偲愗曅宍偲側傞丅1師幃傪堷偔傢偗偩偐傜僌儔僼偺奐偒偼曄傢傜側偄丅2師偺崁偺學悢傪a偲偡傞偲丄愗曅宍偺曽掱幃偼偳偆側傞丅
亙傑側傇亜揰B丆C偺x嵗昗偐傜丄y=a(x-2)(x-5)偱偡丅
亙愭丂惗亜偦偆丄偙偺愗曅宍傪婎弨偵偟傛偆丅偦偆偡傞偲媮傔傞曽掱幃偼偳偆偍偗偽偄偄丅
亙偐偢巕亜偼偄丄媡偵2x+1暘偩偗y幉曽岦偵忋偘傟偽偄偄傫偩偐傜丄
丂丂丂y=a(x-2)(x-5)+2x+1
偲側傝傑偡丅偁偲偼丄a傪媮傔傞偨傔偵丄揰A偺嵗昗傪戙擖偡傟偽偄偄傫偱偡偹丅
丂18a-1=35 傛傝a=2, 偩偐傜丄y=2(x-2)(x-5)+2x+1=2x2-12x+21
丂傊乕偭丄愭惗丄弌棃傑偟偨丅
亙愭丂惗亜偄傑偼丄2揰B丆C偱媮傔偨傢偗偩偗偳丄偱偼丄帋偟偵崱搙偼A丆B偱寁嶼偟偰偛傜傫丅
亙傑側傇亜傏偔偑傗傝傑偡丅
丂傑偢丄捈慄AB偺曽掱幃偺孹偒偼-10傛傝捈慄偺曽掱幃偼
丂丂丂y=-10(x-2)+5=-10x+25
丂偩偐傜丄媮傔傞曽掱幃偼丄
丂丂丂y=a(x+1)(x-2)-10x+25
偲偍偗傑偡丅嵟屻偵揰C傪戙擖偟偰丄18a-25=11 傛傝a=2
丂埲忋傛傝丂y=2(x+1)(x-2)-10x+25=2x2-12x+21
丂惁偄偱偡偹丅娙扨偵媮傑偭偪傖偆傫偩丅
亙愭丂惗亜3揰捠夁偺栤戣偼丄曻暔慄忋偺2揰偱愗曅偑寛傑傞偙偲傛傝丄偙偺2揰偑僌儔僼偺暆傪昞偟偰偄傞偙偲偵側傞丅偦偟偰巆傝偺1揰偱丄愗曅偐傜捀揰傑偱偺崅偝偑寛傑傝丄奐偒偑妋掕偡傞偙偲傪昞偟偰偄傞傢偗偩丅偙傟偱丄傑側傇偺扨弮偵悢抣傪戙擖偟偰媮傔偰偟傑偆偙偲傊偺晄枮偼夝徚偱偒偨偙偲偵側傞偹丅
| 亂惈丂幙亃 丂曻暔慄y=ax2偵暯峴偱丄2揰A(兛,f(兛)),B(兝,f(兝))傪捠傞曻暔慄偺曽掱幃偼丄捈慄AB偺曽掱幃傪y=g(x)偲偡傞偲丄 丂丂丂f(x)=a(x-兛)(x-兝)+g(x) 偱梌偊傜傟傞丅 |
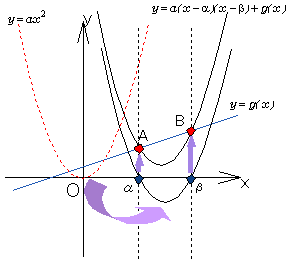 丂曻暔慄偺曽掱幃傪f(x)=ax2+bx+c偲偟傑偡丅
丂曻暔慄偺曽掱幃傪f(x)=ax2+bx+c偲偟傑偡丅
丂捈慄AB偺曽掱幃偼丄
丂丂丂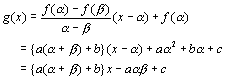
傛偭偰丄
丂丂丂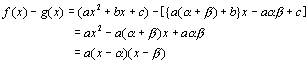
丂埲忋傛傝丄丂丂丂 f(x)=a(x-兛)(x-兝)+g(x)
| 丂ex1) y=3x2偱丄2揰A(1丆2)丆B(4丆5)傪捠傞曻暔慄偺曽掱幃傪媮傔傛丅 丂夝)丂捈慄AB偺曽掱幃偼丄y=x+1傛傝丄媮傔傞曻暔慄偺曽掱幃偼丄 丂丂丂y=3(x-1)(x-4)+x+1 丂丂丂丂亪 y=3x2-14x+13 |
丂師偵丄愗曅宍偲丄堦斒宍丄昗弨宍偲偺娭學傪傒偰傒傑偟傚偆丅
(1)愗曅宍佁堦斒宍
丂堦尵偱偄偆偲丄乽夝偲學悢偺娭學乿偲偄偆偙偲偵側傝傑偡丅
丂偙偺娭學帺懱偑愗曅宍偐傜摫偐傟偨傕偺偱偁傝丄偦偺棙梡朄偑憡屳偺曄姺傪昞偟偰偄傑偡丅
(2)愗曅宍佁昗弨宍
丂f(x)=a(x-兛)(x-兝)丂偲偡傞偲丄曻暔慄偺幉偺曽掱幃偼丄偦偺懳徧惈偐傜柧傜偐偵
丂丂丂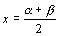
偲側傝傑偡丅傑偨丄捀揰偺y嵗昗偼丄偙偺抣傪戙擖偟偰傕媮傔傜傟傑偡偑丄f(x)偺僌儔僼偺奐偒偐傜丄捀揰偐傜愗曅偺抣偺憹尭傪丄
丂丂丂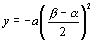
偲撉傒庢傞偙偲偑偱偒傑偡丅埲忋傛傝丄
丂丂丂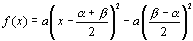
偲昗弨宍傊偺曄宍偑姰惉偟傑偡丅昗弨宍偐傜愗曅宍偼擇忔嵎偺場悢暘夝偺岞幃傛傝摼傜傟傑偡丅
丂偱偼丄x幉偲偺岎揰偑側偄応崌偱偡偑丄偙傟偼悰尨儗億乕僩偵嫆傝傑偡丅
丂丂丂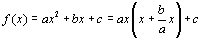
傛傝丄
丂丂丂幉偺曽掱幃偼丄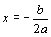 丄捀揰偺y嵗昗偼丄
丄捀揰偺y嵗昗偼丄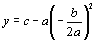
偲側傝傑偡丅
丂偙偺傛偆偵丄擇師娭悢偺嶰懺偼梕堈偵懠偺宆傊偲曄姺偑壜擻偵側傝傑偡丅婎杮揑偵偼慜弎偟偨傛偆偵丄暯柺忋偺2揰偑梌偊傜傟偰偄傟偽丄愗曅宍偐傜偺傾僾儘乕僠偑壜擻偲偄偊傞偱偟傚偆丅
| 丂ex2) 2揰A(1丆2)丆B(4丆8)傪捠傝x幉偵愙偡傞曻暔慄偺曽掱幃傪媮傔傛丅 丂夝)丂捈慄AB偺曽掱幃偼丄y=2x偱偁傞偐傜丄 丂丂丂丂丂 y=a(x-1)(x-4)+2x=ax2+(-5a+2)x+4a 丂丂偲偍偗傞丅塃曈=0偺敾暿幃傪D偲偡傞偲丄 丂丂丂丂丂丂D=(-5a+2)2-16a2=(a-2)(9a-2) 丂丂x幉偲愙偡傞偐傜D=0傛傝丄a=2丆2/9 傪摼傞丅 |
丂傑偨丄愗曅宍偼丄杮棃丄曻暔慄偲掕悢捈慄偲偺岎揰偺堄偱偡偐傜丄愗傝庢傜傟偨尫偺挿偝偵娭學偡傞栤戣偼愗曅宍偺椞暘偵側傝傑偡丅
| 丂ex3) 曻暔慄y=x2-2ax+a+1 偑x幉偐傜挿偝2偺慄暘傪愗傝庢傞偲偒丄a偺抣傪媮傔傛丅 丂夝) 幉偺曽掱幃偼丄x=a偱偁傞偐傜丄愗曅偺x嵗昗偼丄a-1,a+1偱偁傞丅 丂丂y=0偲偡傞擇師曽掱幃偵偍偄偰丄夝偲學悢偺娭學傛傝丄 丂丂丂丂丂丂(a-1)(a+1)=a+1 亪丂丂a=-1,2 |
| 丂ex4) y=2x2-3x+1 傪尨揰傪捠傞傛偆偵暯峴堏摦偟偨曻暔慄偺曽掱幃傪媮傔傛丅 丂夝) y=(x-1)(2x-1) 傛傝丄x愗曅偺x嵗昗偼 x=1,1/2丅傛偭偰丄愗傝庢傜傟傞尫偺挿偝偼 1/2丅 丂丂傑偨丄僌儔僼偺奐偒偼2偱偁傞偐傜丄 丂丂丂丂丂丂 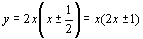 |
丂偲偙傠偱丄愗曅宍偱偼捠夁2揰偐傜丄僌儔僼偺奐偒埲奜偺梫慺偑妋掕偱偒傑偡丅偦偟偰丄巆傝1揰傪戙擖偡傞偙偲偱丄僌儔僼偺奐偒傪妋掕偟丄曻暔慄偑寛掕偡傞傢偗偱偡偑丄偱偼捠夁3揰偐傜嵟弶偵僌儔僼偺奐偒傪妋掕偡傞偙偲傪嵟屻偵峫偊偰傒傑偟傚偆丅
丂偲傝偁偊偢丄捠夁3揰A(兛丆f(兛))丆A(兝丆f(兝))丆C(兞丆f(兞))傪捠傞曻暔慄偺曽掱幃傪扨弮偵戙擖偡傞偙偲偱媮傔偰傒傑偡丅
丂曻暔慄偺曽掱幃傪f(x)=ax2+bx+c偲偟丄3揰傪戙擖偟傑偡丅
丂丂丂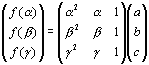
傛傝丄
丂丂丂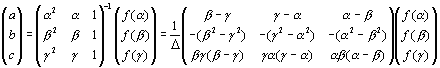 丂乧乧乧(仏)
丂乧乧乧(仏)
丂偙偙偱丄
丂丂丂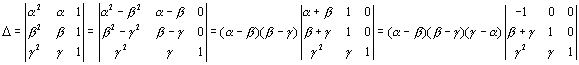
丂傛偮偰丄
丂丂丂嚈亖亅(兛亅兝)(兝亅兞)(兞亅兛)
丂偙傟偐傜(仏)偵3揰傪戙擖偡傞偙偲偱丄擇師娭悢偺奺崁偺學悢a,b,c偑摼傜傟傑偡偑丄幚嵺偺栤戣偱偼偙傫側寁嶼偼柺搢側偽偐傝側傫偺栶偵傕棫偪傑偣傫丅
丂偨偩丄僌儔僼偺奐偒傪昞偡a偺抣傪傒傞偲丄
丂丂丂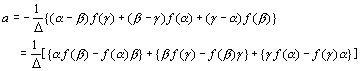
偲曄宍偡傞偙偲偑偱偒傑偡丅
丂偙偺寁嶼傪師恾偺傛偆偵儌僨儖壔偟偰傒傑偟傚偆丅丄僌儔僼偺奐偒偑儕僘儉僇儖偵寁嶼偱偒傑偡丅
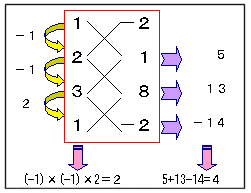 丂
丂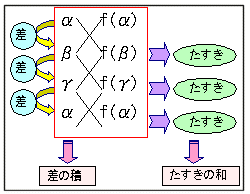
丂椺偊偽丄師偺栤戣丅
| 丂ex5) 3揰A(1丆亅2)丆B(2丆1)丆C(3丆8)傪捠傞曻暔慄偺曽掱幃傪媮傔傛丅 丂夝) 3揰A(1丆亅2)丆B(2丆1)丆C(3丆8)傪捠傞曻暔慄偺僌儔僼偺奐偒a偼丄 丂丂丂丂丂(暘曣)亖(1亅2)(2亅3)(3亅1)亖2 丂丂丂丂丂(暘巕)亖(1亄4)亄(16亅3)亄(亅6亅8)亖4 丂丂傛偭偰丄a=2傪摼傞丅 丂丂傑偨丄2揰A丆B傪捠傞捈慄偺曽掱幃偼丄y=3x-5傛傝丄曻暔慄偺曽掱幃偼丄 丂丂丂丂丂y=2(x-1)(x-2)+3x-5 丂丂丂丂丂丂亪丂y=2x2-3x-1 |