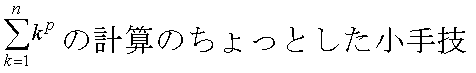
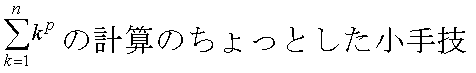
<先 生>
ex) 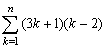 を計算せよ。 を計算せよ。
|
よしお、やってご覧。
<よしお>
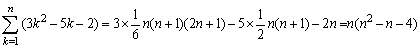 となります。
となります。
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<かず子>
<まなぶ>
<かず子>
<まなぶ>
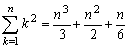
<よしお>
<先 生>
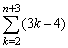
<かず子>
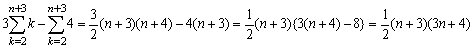
<よしお>
<かず子>
<先 生>
<まなぶ>
<先 生>
<よしお>
<先 生>
<かず子>
<先 生>
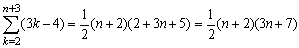
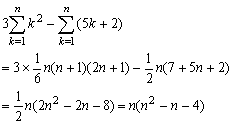
<まなぶ>
<先 生>
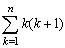
<まなぶ>
<先 生>
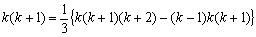
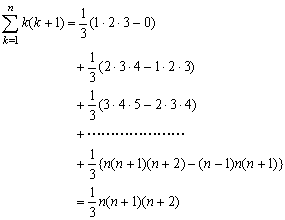
<まなぶ>
<よしお>
<先 生>
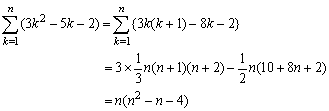
<まなぶ>
<先 生>
<よしお>
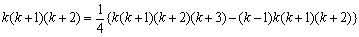
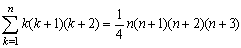
<先 生>
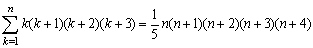
<よしお>
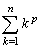 の公式は必要なくなるというわけですよね。
の公式は必要なくなるというわけですよね。
<先 生>
<まなぶ>
<先 生>
<まなぶ>
<よしお>
<まなぶ>
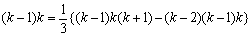
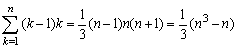
<先 生>
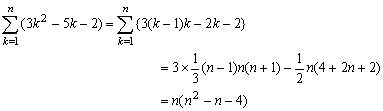
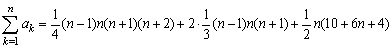
<かず子>
<まなぶ>
<先 生>
<まなぶ>
<先 生>
<よしお>
<先 生>
<かず子>
<先 生>
<まなぶ>
<先 生>
<生徒達>
<先 生>
<よしお>
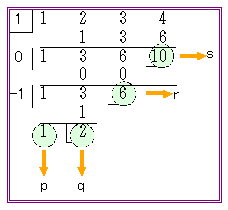 <先 生>
<先 生>
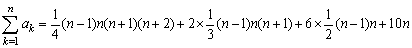
<まなぶ>
<先 生>
<まなぶ>
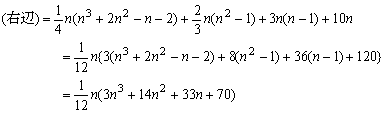
<先 生>
<まなぶ>
あとがき
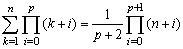
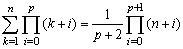
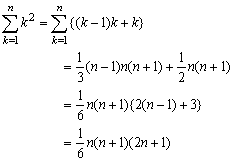
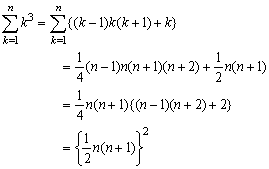
 次に、k4ですが、これはちょっと工夫が必要です。
次に、k4ですが、これはちょっと工夫が必要です。
k4=(k4-k2)+k2=(k-1)k(k+1)k+k2=(k-1)k(k+1)(k+2)-2(k-1)k(k+1)+k2
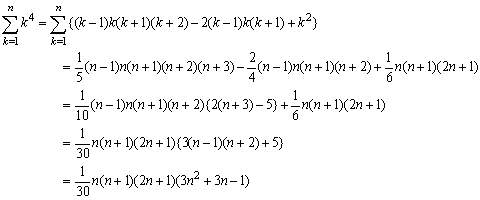
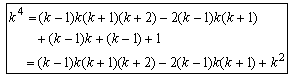
同様に、
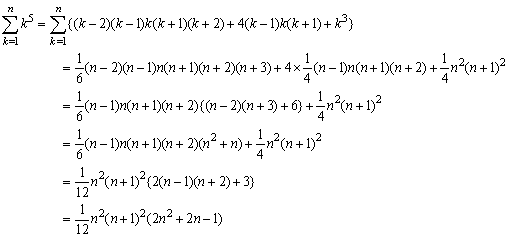
k5=(k5-k3)+k3=(k-1)k(k+1)k2+k3=(k-1)k(k+1)(k2-4)+4(k-1)k(k+1)+k3
=(k-2)(k-1)k(k+1)(k+2)+4(k-1)k(k+1)+k3
さて、ところで、上述の方法は、連続する整数の積を利用して和を求めているわけですが、奇数のベキ和に関しては、もっと巧く和を求めることができます。
k2(k+1)2-(k-1)2k2=k2{(k+1)2-(k-1)2}=4k3
このように、連続する2つの平方数の積を作ると、
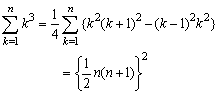
k3(k+1)3-(k-1)3k3=k3{(k+1)3-(k-1)3}=k3(6k2+2)=6k5+2k3
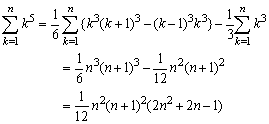
k4(k+1)4-(k-1)4k4=k4{(k+1)4-(k-1)4}=k4(8k3+8k)=8k7+8k5
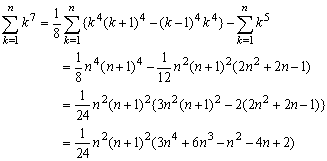
k5(k+1)5-(k-1)5k5=k5{(k+1)5-(k-1)5}=k5(10k4+20k2+2)=10k9+20k7+2k5
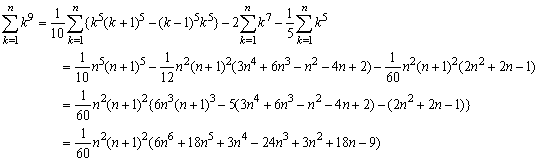
この変形により奇数のベキ和に関しては、容易に求められることがわかります。
では、偶数のベキ和はどうすればいいのでしょう。エレガントな求め方をしっている人がいたら教えて下さい。
なお、このベキ和の問題は、上述の解法をみても帰納的定義、二項定理が絡んでいることが分かります。それを発展させた形としてスイス人のベルヌーイはその著書「確率論」で次のようにベキ和についてまとめています。
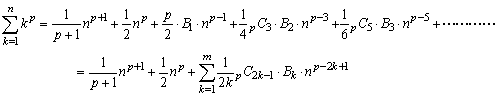
ここで、pが偶数のときは、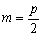 でありpが奇数のときは、
でありpが奇数のときは、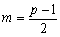 となります。
となります。
また、係数Bkはベルヌーイ数とよばれ、逐次pに数値を代入していくとその値が得られますが、次の関係式でも知られています。
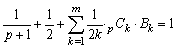
さて、これらの式から、pのベキ和はnに関するp+1の高次式となり、np+1,npの係数はそれぞれ、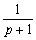 ,
,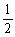 であり、最後の項はpが偶数のときは2次、pが奇数のときは1次式であることが分かるでしょう。
であり、最後の項はpが偶数のときは2次、pが奇数のときは1次式であることが分かるでしょう。
ところで、本文中、ベキ和については何の共通性もない云々の説明を先生がしていますが、それは生徒にとっては背景が難しすぎるという意味で共通性、発展性が見えないというだけです。ここから生まれるベルヌーイ数は無限級数の和においても中核的な働きをしていきます。すべてはベキ和から始まったといえるでしょう。