

|
ex)△ABCにおいて、次の値を求めよ。 (1) b=4,A=60°,B=45°のとき、辺aの値。 (2) B=60°,b= 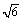 ,c=2のとき、角Cの値。 ,c=2のとき、角Cの値。(3) a= 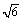 ,b=2,c= ,b=2,c=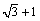 のとき、3つの内角A,B,Cの値 のとき、3つの内角A,B,Cの値
|
<よしお>正弦定理を使ってと問題でいってるんだから、簡単ですよね。
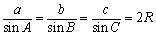 ……(*)
……(*)
に代入すれば、答えがででくる。
<まなぶ> そうだよな。これが単に残りの辺と角を求めよって問題だと、正弦定理を使うんだかそれとも余弦定理を使うんだかごちゃごちゃになって、訳が分からなくなるものね。
<かず子>でも、私は正弦定理は苦手だな。途中で繁分数の計算がでてきて計面倒なんだもの。
<先 生>それじゃあ、かず子、(1)を解いてごらん。
<かず子>もう!、先生意地悪なんだから。……正弦定理に与えられている値を代入すると、
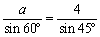
だから、
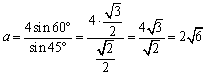
となります。
<まなぶ>まあ、計算の煩わしさはあるけどいつもの先生の問題からすると随分ストレートな問題ですね。
<先 生>いいタイミングの感想だ。実は今日のテーマは、三角形の解法において正弦定理を利用できるのはどんな場面であるかということと、分数の繁雑さはどう解消したらいいかということなんだ。先ほど、まなぶとかず子が漏らした感想に応えるということだね。
<まなぶ>さすが先生。生徒の気持ちをよく理解していらっしゃる。
<先 生>こそばゆいようなお世辞はいいから。さて、そのためにはまず正弦定理って何かということを、もう一度確認してみよう。
<かず子>先ほどよしおがいった定理(*)のことじゃないんですか。
<よしお>その公式がどういう意味をもっているかということですよね。
<かず子>確か正弦定理の証明は、円の性質である、「弦の円周角が等しい」ということと、「直径を弦とする円周角が90°である」ことから、円に内接する任意の三角形を直角三角形に変形してその正弦を考えたんですよね。
<先 生>その通り。したがって、もともと正弦定理は、
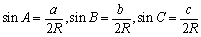
のように、表されていたんだったよね。これを見やすいように一本の形にまとめたものが(*)ということだ。そこでだ。ちょっとこれらの正弦の比を求めてみよう。
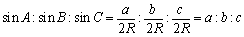
となる。ではこれは三角形の辺と角がどういう性質を表しているということだろう。
<まなぶ>三角形のサインの比は、辺の長さの比に等しいということですか。
<先 生>角Aと辺aの位置関係を考えて、もう少し正確に表現してごらん。
<よしお>対辺、対角の関係ですよね。そうすると、
辺の長さの比は対角の正弦の比に等しい
ということですか。
<先 生>そう、これが正弦定理の原理を表していることになる。そしてそのことから正弦定理がどんな場面で使えるかということも分かってくる。辺とその対角の関係を表すわけだから、三角形の要素として辺と対角が1組以上与えられていれば正弦定理を使える可能性がでてくる。
では、そう考えると(1)はどう計算できるだろう。
<かず子>A,B,bが与えられているから、sinA:sinB=a:bということですよね。
そうすると、
sin60°:sin45°=a:4
ここで、内項の積と外項の積は等しいから、
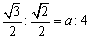 より、
より、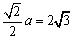 から、
から、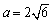
となります。本当だ。少し計算が簡単になったような気がする。
<先 生>あるいは、
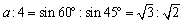
よりaを求めるとさらに楽だね。では(2)はどうだろう。
<まなぶ>僕がやります。Bとbは辺と対角の関係だから正弦定理が使えそうだということですね。
sinB:sinC=b:cより、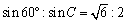
よって、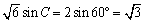 より、
より、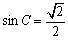
∴ C=45°
となります。
<先 生>まなぶ、C=135°は駄目なのかい。
<まなぶ>先生、騙されませんよ。だって、C=135°なら、B+C=195°>180°となって、三角形が作れないじゃないですか。
<先 生>そうも考えられるね。でも角Cを求めなくても、b>cからB>Cとなるからすぐ分かるんだよ。さあ、最後の(3)にチャレンジしよう。
<生徒達>………
<よしお>先生、これは3辺が与えられた場合だから余弦定理を使って3つの角を求めるのではないのですか。
<先 生>そうだよ。
<まなぶ>あのね。先生、最初に今日は正弦定理を使って問題を解こうっていってたじゃないですか。
<先 生>そうだよ。でも正確にいうと「正弦定理を利用して」といったはずだけど。
<かず子>どこが違うのですか。
<先 生>ではみんなに聞くけど、余弦定理を使って3つの角を求めるとき、どの角を計算する?。
<かず子>私は角Cです。辺C=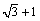 だから、この値が分母にあると計算が面倒だと思うんです。
だから、この値が分母にあると計算が面倒だと思うんです。
<先 生>かず子は計算方法にずいぶん拘っているね。他のみんなは。
<まなぶ>僕はBだな。こういうときって必ず先生は何か企んでいるような気がするするから分母に根号がたくさんある場合を考えます。
<よしお>じゃあ、僕は残りのAにします。
<先 生>それじゃ、実際に計算して貰おうか。かず子からやってごらん。
<かず子>はい。
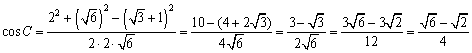
あれ?、ぐちゃぐちゃした値になっちゃったわ。
<まなぶ>ラクな道を進もうとするから落とし穴に引っかかるんだよ。進んで困難に立ち向かっていく姿勢がなくちゃ駄目だよな。
<かず子>何を知った風なこといってんの。角Aだってまだ求められるって分かったわけじゃないわよ。
<先 生>まあまあ。そのことは正弦定理を利用すると調べることができるんだよ。定理の意味をもう一度考えてごらん。
<よしお>辺の長さの比は対角の正弦の比に等しいでしたよね……、ということは、この場合、
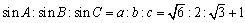
ですね。
<先 生>うん。いい線いってる。ところでだ。三角比の解法においては当然、求めることができる角は限定されているよね。どんな角だろう。
<かず子>鋭角だと30°,45°,60°ぐらいですよね。
<先 生>ではそのときの正弦の値は?
<まなぶ>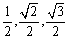 ですね。あっ、そうか。先生の言いたいことやっと分かりました。先ほどのsinA:sinB:sinCの比もこれらの値で表現できなきゃならないということですよね。
ですね。あっ、そうか。先生の言いたいことやっと分かりました。先ほどのsinA:sinB:sinCの比もこれらの値で表現できなきゃならないということですよね。
<先 生>その通りだ。ちょっと、予想してごらん。
<まなぶ>思うに、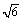 が曲者ですね。
が曲者ですね。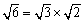 だから、これが
だから、これが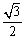 になりそうな気がする。
になりそうな気がする。
だから、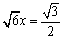 とすると、
とすると、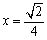 。これを比の値にかけると、
。これを比の値にかけると、
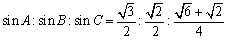
ばっちしです。AとBの角が求められます。
A=60°,B=45°ですね。
<かず子>A,Bが鈍角の場合も考えなくちゃいけないんじゃない。
<よしお>いや、必要ないよ。c>a>bだから、C>A>Bとなる。鈍角になる可能性があるのは角Cだけだよ。Cは、
C=180°-A-B=75°
で確かに最大角になっている。
<まなぶ>へぇっー、本当に正弦定理で解けちゃったよ。
<先 生>いや解けてない。
<まなぶ>先生、そのバサッと切り捨てるような言い方、やめてくれない。なんの問題があるんですか。
<先 生> (3)の問題の場合、3辺の長さが与えられているから三角形は決定している。だから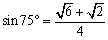 ということをしっていれば、これらの角が比を満たしているわけだから、解答とすることはできる。でも、みんなは の正弦の値は知らないだろう。それがはっきりしないのであれば結局、答えを予想したに過ぎないんだ。
ということをしっていれば、これらの角が比を満たしているわけだから、解答とすることはできる。でも、みんなは の正弦の値は知らないだろう。それがはっきりしないのであれば結局、答えを予想したに過ぎないんだ。
<かず子>なんとなくわかりましたけど、ということは、結局は余弦定理を使って求めなくちゃいけないんですか。
<先 生>そう、その通り。ただし、どの角に対して余弦定理を使うかという段階で実は間接的に正弦定理の性質を利用しているんだ。この場合、かず子が求めようとした角Cは、その対辺がc=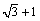 なんだから、この値に対応する角が求められないのは容易に予想ができるだろう。かず子はそこのところの読みを誤ったということだ。これに対してA,Bはその対辺から求められそうな値になっているね。では験しに、まなぶ、Aを求めてごらん。
なんだから、この値に対応する角が求められないのは容易に予想ができるだろう。かず子はそこのところの読みを誤ったということだ。これに対してA,Bはその対辺から求められそうな値になっているね。では験しに、まなぶ、Aを求めてごらん。
<まなぶ>えへん!。はい、
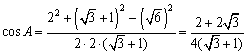
あとは、分母の有理化ですね。
<先 生>まなぶ、そんな必要あるだろうか。何度もいうけど正弦定理から角度の予想はもうできているんだよ。
<かず子>先生、私分かるわ。分母の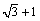 は有理化しなくたって消えなきゃ角度は求められないってことですよね。
は有理化しなくたって消えなきゃ角度は求められないってことですよね。
だから、
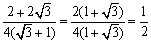
cosA=1/2より、A=60°だわ。
<まなぶ>かず子、横取りするなよな。
<よしお>じゃあ、最後にBを僕が求めてみます。
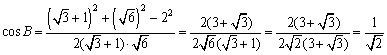
∴ B=45°です。
<先 生>正弦定理を辺の比として捉えると、いろいろなことが見えてきて、その効用を最大限活かすことができるんだ。三角形の解法問題では、余弦定理を使う機会の方が圧倒的に多いわけだけど、それを根底でしっかりと支えているのが正弦定理なんだよ。
<まなぶ>僕達のいままでの正弦定理の使い方は、その効用がセイゲン(制限)されていたということですね。
<先 生>くだらん!。
<まなぶ>また切り捨てた。
佐藤一昭先生(別海高校)は、分数計算が不得意な生徒に対して、正弦定理を
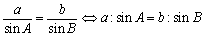
として、比で表し計算をラクにすることで、三角形の要素を求められる喜びを生徒に提供しようとするものでした。
松本 啓先生(蘭越高校)は、関数電卓を生徒全員に持たせて、
対辺÷sin
の値を計算させて、みな同じような値になることから、その値が外接円の直径であることを予測させたり、いろいろな性質を考えさせようとするものでした。
 奇しくも同じ正弦定理に関するレポートが出たのは、三角比が数Ⅰの単元としては1年で学習する内容の後半の山場であり、授業で取り組んだ「ほかほかの悩みたての問題」であったからと推察します。それほどに三角比は理解して欲しいのに生徒の理解が空回りしてしまう分野といえます。
奇しくも同じ正弦定理に関するレポートが出たのは、三角比が数Ⅰの単元としては1年で学習する内容の後半の山場であり、授業で取り組んだ「ほかほかの悩みたての問題」であったからと推察します。それほどに三角比は理解して欲しいのに生徒の理解が空回りしてしまう分野といえます。
数Ⅰで初めて登場する幾何であるわけですが、幾何が「補助線のような発想」を要求することに対して,その対処として機械的に要素を計算する道具である三角比が登場したにも関わらず、その便利なツールを使いこなせない生徒が多いのが現状といえるのです。
そのとっつき難い要因の一つは直角三角形の2辺の間に成り立っていた比である三角比が、図形の計量のときには、任意の三角形において、正弦、余弦定理として拡張されるからでしょう。加えて、正弦・余弦といった用語と三角比の性質がどうも結びつかないのです。なぜ、正弦なのでしょうか。そのことを暗に啓発してくれた研究レポートであったかと思います。
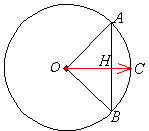
 ところで三角比はもともと天体の星の間の距離を計測する三角測量(三角法)としてギリシアで考案され、インドに伝えられてアールヤバタ(6世紀頃)によってサインの記号が使われたといわれています。
ところで三角比はもともと天体の星の間の距離を計測する三角測量(三角法)としてギリシアで考案され、インドに伝えられてアールヤバタ(6世紀頃)によってサインの記号が使われたといわれています。
右図の弦ABとその弧で作られる図形を弓とみなし、矢であるOCを引っ張ったときに、弦ABを切ってできる半弦AHをサイン(弓の弦:diya)としたのです。
アールヤバタの天文学の書物はやがてアラビアに渡り、ラテン語に翻訳され(sinus)、さらに欧州に伝わり現在の記号sineに訳されます。
その後、cosine(ニュートン)やtangent(トーマス・フィンケ)といった三角比の仲間達も考え出され、シルクロードを通って中国へと伝えられます。そして、除光啓によって漢訳されたとき、正弦、余弦、正切(接ではなく、弦を切るという意味での切)という用語が初めて使われるようになるのです。
したがって、もともとは直角三角形の比ではなく、半弦によって作られる比であったわけです。そういった伝来の背景(なんと壮大な旅なのでしょうか)は残念ながら授業の中で触れる機会は少ないわけですから、正弦定理の名前およびその証明についても何か違和感が生じてしまうのです。
そして、それは証明において任意の三角形を強引にでも直角三角形に帰着させて考えるとという妙な固執に顕れている感じもします。
そこで、弦の性質から正弦定理を見直してみましょう。
正弦の弦を「三角形の外接円」と捉えず、単なる1つの円の弦としましょう。このとき、正弦定理は次のように表現できます。
| 弦の長さの比は円周角の正弦の比に等しい |
 このことを証明してみましょう。
このことを証明してみましょう。
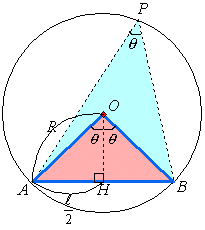
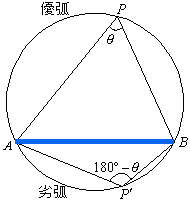
半径Rの円の弦ABの長さをl、優弧上の点Pに対してその円周角をθとします。すなわち、∠APB=θ。
このとき、円の中心を とすると、中心角は∠AOB=2θとなります。中心Oから弦ABに下ろした垂線の足をHとすると、直角三角形OAHにおいて、∠AOH=θ,AH=l/2ですから、
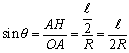
∴ l=2Rsinθ
を得ます。
また、劣弧上に点P'がある場合は、
∠APB+∠AP'B=180° (補角)
ですから、
sin∠AP'B=siin(180°-∠APB)=sinθ
より、劣弧上の円周角についても同様の結果となります。
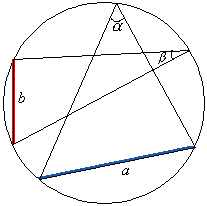
以上より、2つの弦の弧の長さをそれぞれa,b、その円周角をα,βとすると、a=2Rsinα, b=2Rsinβ ですから、
a:b=sinα:sinβ
となります。
また、円の半径Rについても、一つの弦とその円周角が与えられたときは、直径を弦とする円周角は90°であることから、
a:2R=sinα:sin90°=sinα:1
を満たすRを考えれば求められることになります。
このように考えると正弦定理は必ずしも三角形上で成立する必要はないわけです。円周上の異なる3点で作られる3つの弦を辺とするような三角形を作ったときに、教科書で示されるような「三角形の内角における正弦定理」となると考えた方が自然といえるでしょう。
したがって、三角形ABCにおいては、正弦定理は、
| a:b:c=sinA:sinB:sinC |
と表現する方が、正弦の本質を表していることになるわけです。
小手技の本文中では、「辺と対角の正弦の比」という表現で説明していますが、これもまなぶのいうようにセイゲン(制限)された解釈であるわけです。
では、余弦についても同様に円の弦として考えてみましょう。
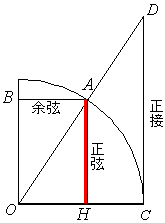
もともと、余弦は、余角(和が90°である関係)の正弦ですから、直角三角形で成立する三角比では、一つの角θに対して、90°-θの正弦を表します。
すなわち、
cosθ=sin(90°-θ)
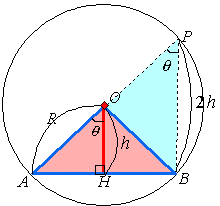
となるわけです。これを単位円での半弦AHで考えると、右図のOHが余弦を表しており、これは、円の中心と半弦との距離を意味します。
円の半径Rとし、円周角がθである弦に対して、円の中心から弦までの距離をhとすると、
cosθ=h/R より、 h=Rcosθ
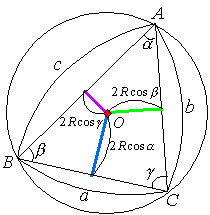
これから、余弦定理は、
| 円の中心と弦までの距離の比は、円周角の余弦の比に等しい |
と表されます。
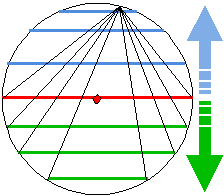 このことは、弦の長さとその円周角は優弧上では、弦が長くなれば円周角も大きくなることから、鋭角では、余弦の値が大きくなれば角が小さくなることが分かります。また、劣弧上では、中心と弦との距離に方向を考えれば負の値になることも説明がつけられるわけです。
このことは、弦の長さとその円周角は優弧上では、弦が長くなれば円周角も大きくなることから、鋭角では、余弦の値が大きくなれば角が小さくなることが分かります。また、劣弧上では、中心と弦との距離に方向を考えれば負の値になることも説明がつけられるわけです。