

����@�����ȂɁI�A�Ȃp�����������Ƃ������̂��H
�������q���ǂ������́A�搶�A����Ȃɑ傫�Ȑ��o���āB�������������̂́u���������v�̂��ƂȂ́B
����@�����w���A�ΐ��̂��������H
�������q�������A����B�ΐ����ĉ��҂Ȃ�ł��傤���B
����@���������Ԃ�A�ΐ��Ɏ���Ȍ��������ȁB�ΐ��́AN=aM�̂Ƃ���M�����߂鎮�Łc�c�B
�������q���搶�A����͕������ł��B�搶�����ƂŐ������Ă��ꂽ���Ƃ͗����ł�����ł����ǁA�ΐ��Ǝw���̈Ⴂ���悭������Ȃ���ł��B�l����l����قǁA�w���Ƒΐ��͓������Ƃ������Ă���悤�ȋC�����Ă��āB
����@���������Ă邱�Ƃ��悭������Ȃ����B
�������q�����ȏ��Ŋm�F���Ă݂���ł��B�w���ɂ��ẮA
�@�@�@�ua�̗ݏ�an�ɑ��āAn�����̗ݏ�̎w���Ƃ����v
���������Ă��܂����B���ɑΐ��ł����A
�@�@�@�uap=M �ƂȂ����p��a���Ƃ���M�̑ΐ��Ƃ����v
�ƂȂ��Ă��܂��B��������ƁAp��M�̑ΐ��Ƃ������Ƃ́AM=ap�ł�����A�ݏ�̎w��������ΐ��Ƃ������Ƃł��傤�B����������A����p�͎w���ɂ��ΐ��ɂ��Ȃ���Ă��Ƃ���Ȃ��ł����B���������ΐ����ĉ��҂Ȃ�ł��傤�B
����@�����Ӂ[��B�ʔ����������ˁB�悵���Ƃ܂ȂԂ͊m�������ɂ�����ˁB�݂�Ȃł��̂��Ƃ��l���Č��悤���B
����@�����c�����q�̋^��͂��܂݂�Ȃɘb�����Ƃ��肾�B�݂�ȁA�����q�̔Y�݂ɕt�������Ă���Ȃ����낤���B�܂��A�ΐ��Ǝw���̊W���l����O�ɂ�����Ǝ��̖�������Ă��炨�����B
|
ex) ���̕��͂�he�����ɂ��ď���������B �@�@�@She loves him |
���܂Ȃԁ��搶�A���������ǂ������́B�ΐ��̕������Ȃ�������ł����B
����@�������̂��肾��B�܂ȂԁA�����������Ă����B
���܂Ȃԁ��搶�A�ڂ��͐��w���p��̕������ӂ��Ă��ƒm���Ă܂����B�\���Ԃ��Ԃɏ�����������Ă��Ƃł���B
| He is loved by her |
����@�����܂��A�m���ɐ��w���̓X���X�������Ă���ˁB
�������q���܂ȂԂ̂��ƁA������ƌ���������B�ł��搶�A���ꂪ�w���E�ΐ��Ƃ��������ǂ�ȊW�������ł����B
����@�������́A�w���Ƒΐ��̊W�����̉p���̏��������Ɠ����Ȃ�B�܂�A�ݏ�aM�̒l��N�ł���Ƃ��A
�@�@�@N=aM
�Ƃ������Ƃ����ǁA�������{��ɖƁA
�@�@�@�uN ��a��M�悵�����̂ł���v
�����̕��т� N�Ca�CM�̏��ɖ|��Ƃ����Ȃ�B�ł͏��Ԃ��t�ɂ���M�Ca�CN�̏��ɓǂނƂǂ��Ȃ邾�낤�B
���悵�����uM��a��ݏ悷���N�ƂȂ�l�ł���v�Ƃ������Ƃł��傤���B
���܂Ȃԁ��ݏ悪M���Ă��Ƃ����炿����ƕ\������������������ǂ����Ȃ邾�낤�ȁB
����@�������{��Ŗ��Ƃ���Ɗm���ɖ��������邩������Ȃ����A���̊W�͌��̎��ɑ��Ă͎�g�̎��ɂȂ��Ă��邱�Ƃ͕����邾�낤�B�p��ɂ�����\���ԂƎԂ̊W�́A�����ɂ��Ă�ex)�ł́A
�@�@�@love �� is loved by
�ƂȂ�A����love���ube����+�ߋ�����+�O�u���v�Ə���������킯���B����𐔎��ł������悤�ɍl���Ă��B���Ȃ킿�u�ݏ悷��v�Ƃ����������A
�@�@�@a���@�ˁ@loga��
�ƕω�������B�����āAM�Ca�CN�̏��Ԃɍ��x�͎���ǂ�ł����ƁA
�@�@�@M�Ca�CN�@�ˁ@M=logaN
���̎Ԃ̌`�ŕ\�����ꂽ���M���ΐ��ȂB
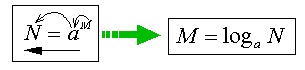 �Ⴆ�A
�Ⴆ�A
�@�@�@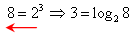
�Ǝ�g�ɂ����Ƃ���log28���ΐ��Ƃ������Ƃ��B
���܂Ȃԁ��{�����B�ЂƂ̕��@�Ƃ݂Ă��܂��͊ȒP�ɕό`�ł������ł��ˁB
�@�@�@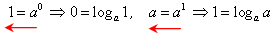
����B�ꔭ���B
����@�����������A�E�ӂ͑ΐ���ݏ�̌v�Z���ʂł���l�ɂ��Ă����Ȃ��Ɠǂݑւ��͂ł��Ȃ����璍�ӂ��悤�B
�Ƃ���ł��܂܂ȂԂ��ǂݑւ������͑ΐ��v�Z�̊�{�ƂȂ���̂��B���ł����炱�̎�g���@�Ŏw���@�����ΐ��@���ł͂ǂ��\������邩�l���Č��悤���B
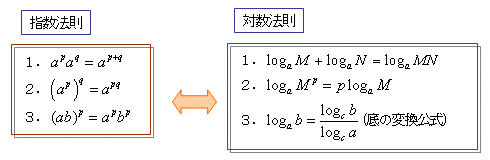
���ꂪ�A�w���E�ΐ��@���������ˁB�ł͎w���@���P���珇�Ɏ�g�ɂ��Ă����Ă݂悤�B
�܂��A���ӂ�
�@�@�@M=ap�CN=aq
�Ƃ����B
���悵�����������g�ɓǂݑւ���킯�ł��ˁB
�@�@�@p=logaM�Cq=logaN�@ �@�c�c�@
�ƂȂ�܂��B
����@���������Ŏw���@���P�́AMN=ap+q�ƂȂ邩�炳��ɓǂݑւ��Ă��B
�������q�� p+q=logaMN�ƂȂ��B�����Đ�قǂ̓ǂݑւ������@�������ďI���ˁB
���悵�����w���@���P��ǂݑւ�����ΐ��@���Q�ɂȂ��ł��ˁB
���܂Ȃԁ��w���@���Q�̎��͖l����낤�B
�@�@�@M=ap
�Ƃ����Ď�g�ɂ���ƁA
�@�@�@p=logaM �@�c�c�A
���̎���Mp=apq�����炱����܂���g�ɂ��āA
�@�@�@pq=logaMq
�A�������ďI���B�ΐ��@���Q�ɂȂ������B
����@�����Ō�͎w���@���R���B�܂ȂԂ��Q�Ԃ�����Ă��܂�������A���傤���Ȃ��A���̖��͂����q�ɍl���ĖႨ�����B
�������q���搶�͉����܂ȂԂɂ���ė~���������݂����ˁB�ł͎�������ɁB
x=ap�Cy=bp�Ƃ����ēǂݑւ���ƁA
�@�@�@p=logax�Cp=logby
�܂��Axy=(ab)p��ǂݑւ��āA
�@�@�@p=logabxy
�݂��p�̎��ɂȂ�����B���̎���g�ݍ��킹�āc�c�c
������A���������ł��Ȃ���B�ǂ����Ă���H�c�c
����������������I
����@���������A���������ȁB�ǂ��ǂݒ����̂��ȁB
�������q����g�̎d��������������Ȃ��āA�搶�����̖����܂ȂԂɂ��������������R�����������Ƃ������Ƃł��B�����āA�ǂ��l���Ă��ǂݑւ����ł��Ȃ��悤�ȋC�������ł����B
���܂Ȃԁ��搶�̍l�������Ȃ��Ƃ���ȁB�ł������q�B�t�ɑΐ��@���R����g�ɂ����炫���Ƃ����������Ă����Ȃ����낤���B
�������q���Ȃ�قǂˁB���Ⴀ�A�܂��E�ӂ�ǂݑւ��Č����B
x=logca�Cy=logcb���w���ɓǂݑւ��āA
�@�@�@a=cx�Cb=cy�@�@�c�c�B
���Ƃ��Ƃ̎��́A
�@�@�@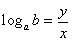 ������A
������A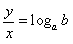
�Ƃ݂ēǂݑւ��āA
�@�@�@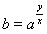
�ŁA�Ō�ɇB�������āA
�@�@�@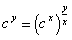
����A�w���R�ɂȂ�Ȃ���B�ǂ����Ă��낤�B
���悵�������̎��͎w���@���Q�ł���ˁB�Ƃ������Ƃ́A�w���@���Q��ǂݒ��������̂��ΐ��@���R�ɂȂ���Ă��Ƃł́B
����@�������̒ʂ�B����͐搶���ϊ����Ă݂悤���B�w���@���Q��
�@�@�@(cx)y=(cy)x �@�@�@�c�c�C
�Ƃ����W�ł��邱�Ƃ��Ӗ����Ă���B�����ŁAa=cx�Cb=cy�Ƃ����A�ǂݑւ���ƁA
�@�@�@x=logca�Cy=logcb
�܂��C���Abx=ay�B�����ǂݑւ��Ay=logabx=xlogab
�@�@�@���@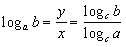
��قǂ悵�����\�z�����ʂ�ΐ��@���R�ɕϊ��ł����ˁB
�������q����������ƁA�w���@���Q�̎��͑ΐ��@���Q�ɂ��R�ɂ��ǂݒ������ł���Ƃ������Ƃł���ˁB����������A�ΐ��@���Q�ƂR�͓��������Ă��ƂɂȂ�܂��B
���܂Ȃԁ��m���ɂ�������ȁB�܂Ă�B�搶�A�Ƃ������Ƃ́A�ΐ��@���Q����R���ؖ��ł�����Ă��Ƃł���ˁB
����@���������`�[�����[�N���ˁB���̒ʂ肾�B�ł�������m�F����O�ɂ�����Ǝ��̎������Ă��炨�����B
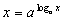
|
���܂Ȃԁ����ł����B���̎w�������ΐ������ς���Ȃ��͂����肵�Ȃ����́B
���悵�����ł��m���ɂ��̎��͐������邵�Ă���ˁB�����ēǂݑւ�������ƁA
�@�@�@logax=logax
�Ƃ���������O�̎��ɂȂ��Ă��܂��B
����@�����������ˁB������O�Ƃ������Ƃ͊ȒP�Ɋm�F�ł���ˁB
���������ڂ����������悤���B
�@�@�@y=logax�@�@�c�c�D
����g�ɂ���ƁA
�@�@�@x=ay�@�@�c�c�E
�����őΐ��D���E�̎w�������ɑ������B����Ɛ�قǂ̎���������B
���܂Ȃԁ��Ȃ�قǁA�Q���ĎԂɂ����猳�̌`�ɖ߂��Ă��܂����Ƃ������Ƃ��B
����@�������̒ʂ肾�B�����A�ł́A��قǂ̂܂ȂԂ̋^��ɉ����Ă悤�B
�ΐ��@���Q�̊W����
�@�@�@logcap=p logca�@�@�c�c�F
�Ƃ��悤�B�����ŁAp=logab �Ƃ����A�F�ɑ������ƁA
�@�@�@(����)=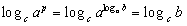
���ꂩ��Alogcb=logab logca ������A
�@�@�@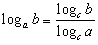
���܂Ȃԁ������B�ł���������B
�������q�����̏ؖ��͋t�ɒH�ꂻ���ł�����ΐ��@���Q�Ƒΐ��@���R�͓��l�Ƃ������ƂɂȂ�܂���ˁB
���܂Ȃԁ�������H�A��������Ǝw���@���R�͂ǂ��Ȃ����Ⴄ�B
�������q���K�v�Ȃ��H���Ă��Ƃł��傤���B
���悵�����ΐ��v�Z�́A�ΐ��@���P�`�R�ł��ׂĉ\�ł���A���ꂪ�w���@���P�C�Q�ɑΉ����Ă���킯������A�m���Ɏw���@���R�͕K�v�Ȃ��Ȃ�܂���ˁB�Ƃ������Ƃ́A�w�w���@���R�́A���@���P�C�Q��蓱�����Ƃ��ł���̂ł͂Ȃ��ł��傤���B
���܂Ȃԁ����ꂶ��A�ǂ����Ă��̎����w���@���P�C�Q�̎��ƕ���Ŗ@���Ƃ��čڂ��Ă�낤�B
�������q������͎w���@�����g���Čv�Z����Ƃ��ɁA�@���Ƃ��Ă����������֗�������Ǝv����B���ꂪ�ΐ��@���ł͓�����O�̌v�Z�ɂȂ��Ă��܂��āA�@���Ƃ��čڂ���K�v���Ȃ������̂ł͂Ȃ��̂�����B
����@���������������Ƃ��ˁB������w���@���R�͑ΐ��@�����g���ΊȒP�ɏؖ��ł���Ƃ������Ƃł�����B���ہA
�@�@�@log10(ab)n=n(log10a+log10b)
�@�@�@�@�@�@�@�@=nlog10a+nlog10b
�@�@�@�@�@�@�@�@=log10an+log10bn
�@�@�@�@�@�@�@�@=log10anbn
���ꂩ�痼�ӂ̐^�����r����Ǝw���@���R�������Ă��܂��ˁB�����߂ł����������B
���܂Ȃԁ��搶�A�҂��Ă�B�܂������q�̎��₪�������Ă��Ȃ���Ȃ��ł����B
�������q��������ˁB�搶���������Ă��ꂽ�̂́A�w������ΐ��ւ̓ǂݑւ�����w���@���ɑΉ�����ΐ��@�����o�����Ƃ������Ƃł���ˁB�ł��A���̕������������̂́A�w���Ƒΐ����ē������Ƃ������Ă���悤�Ɏv����Ƃ������Ƃł��B���̎���̓����͂܂������Ă��Ȃ���H
����@�����ȂA�b�������肾�������ǂˁB��قǁA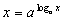 �̏ؖ��̂Ƃ��ɁA�u�ΐ����w�������ɑ���v���Ă�������ˁB����͑ΐ��Ǝw�����������Ƃ��Ӗ����Ă��Ȃ���ł��Ȃ����Ƃ���B
�̏ؖ��̂Ƃ��ɁA�u�ΐ����w�������ɑ���v���Ă�������ˁB����͑ΐ��Ǝw�����������Ƃ��Ӗ����Ă��Ȃ���ł��Ȃ����Ƃ���B
���܂Ȃԁ������Ԃ����Ȃ��f�������Ⴄ��ł��ˁB
�������q���������B����ς莄�̐����͐�����������B�ł��搶�A��������Ƃǂ����āA�u�w���v�Ƃ��u�ΐ��v�Ƃ���ʂ��Ȃ��Ⴂ���Ȃ��́B���ɂ͋�ʂ��邱�Ƃŋp���č����̌���������Ă��܂��Ă���悤�Ɏv�����B
����@�������̂��Ƃɂ��Ă����ɐ����͂��Ă����B
������x�A�ŏ��̘b��ɖ߂낤���B
�\���ԁE�Ԃ̊W�́u�ޏ��͔ނ������Ă���v�Ƃ������ōl�����
�@�@�@(�ޏ�)=(�����Ă�)+(��)�@�@�́@�@(��)=(������Ă���)+(�ޏ�)
�Ƃ������Ƃł���A���ꂪ�w���Ƒΐ��ł�
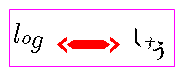
�@�@�@N=aM�@�́@M=logaN
�Ƃ������Ƃ������B���̂Ƃ��A�ΐ�����юw����M�̂��Ƃł���A�p���a��ł́A�ނ̂��Ƃ��B
�����ŁA�p���ł͔\���Ԃ̖ړI��̔�(him)�́A�Ԃł͎��̔�(he)�ɕω����Ă��邾�낤�B�w���E�ΐ��̊W������Ɠ����Ȃ�B����ړI�����ɂ��邩�ɂ���ĕ\�����ω������ƍl��������B����l������Ă��Ƃ͐��w�ł��ƂĂ��d�v�Ȃ��ƂȂB
 �@�ق�A���K���Y���̋L������[���݂Ă����B�������̕����������яオ���Ă��Ȃ����낤���B
�@�ق�A���K���Y���̋L������[���݂Ă����B�������̕����������яオ���Ă��Ȃ����낤���B
�@�w����ΐ��Ƃ��Ă݂邱�Ƃɂ���Ďw���ł͌v�Z�ł��Ȃ������Ƃ������قNJȒP�ɋ��߂���悤�ɂȂ�B���_��ς��Č���ƐV����������������̂ȂB
�@���Ƃ��A�uShe loves him�v���A�Ԃɂ��āA�uHe is loved by her.�v�A�����݂邱�ƂŁA������������悤�ȋC�����Ȃ����ȁA�܂ȂԁB
���܂Ȃԁ��w���Ƒΐ����������Ƃ����Ǔ����g�����ł͂Ȃ����Ƃ͕�����܂����B�ł��A���̉p���͂����������̈Ӗ��������ł��傤���H
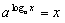
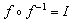 �������Ă���ɉ߂��܂���B�ł́A�w���Ƒΐ��̊W�͂Ƃ����ƁA�ΐ��̌��t�ʂ�A�w���ɑΉ����鐔���ΐ��Ƃ����C���[�W�ő������A�t���̊W�������āA�܂�Ŏw�����t�ɑΉ������������ΐ��̂悤�Ɏv���Ă��܂��̂ł��B��������A�����q�̋^�₪�����܂��B���ۂ́A�u�t�̑Ή��v�Ƃ́A�����u�t�ɓǂݑւ���悤�ȑΉ��v�ł���A�\���Ԃɑ��ĎԓI�Ȍ����ƍl���āA��ꂪ�A���邢�͖ړI�ꂪ�����ɂ���ėp��̎g�����������Ă���ɉ߂��܂���B��̓I�ɂ́A��a�ɑ��āA����n������߂�ꍇ��n���w���ł���An��̒l���^�����Ă���Ƃ��A����n�����߂�ꍇ���ΐ��ł���Ɖ��߂ł��܂��B
�������Ă���ɉ߂��܂���B�ł́A�w���Ƒΐ��̊W�͂Ƃ����ƁA�ΐ��̌��t�ʂ�A�w���ɑΉ����鐔���ΐ��Ƃ����C���[�W�ő������A�t���̊W�������āA�܂�Ŏw�����t�ɑΉ������������ΐ��̂悤�Ɏv���Ă��܂��̂ł��B��������A�����q�̋^�₪�����܂��B���ۂ́A�u�t�̑Ή��v�Ƃ́A�����u�t�ɓǂݑւ���悤�ȑΉ��v�ł���A�\���Ԃɑ��ĎԓI�Ȍ����ƍl���āA��ꂪ�A���邢�͖ړI�ꂪ�����ɂ���ėp��̎g�����������Ă���ɉ߂��܂���B��̓I�ɂ́A��a�ɑ��āA����n������߂�ꍇ��n���w���ł���An��̒l���^�����Ă���Ƃ��A����n�����߂�ꍇ���ΐ��ł���Ɖ��߂ł��܂��B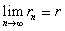 �Ȃ閳���L������ {rn}�ɑ��āA
�Ȃ閳���L������ {rn}�ɑ��āA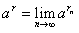 �Ƃ��āA�w�����`���܂����A�m���ɍ��Z���ɑ��Ă͌`���s�ςƂ������Ă��o���Ĕ[�������Ă��܂��A���p�E���p�ɏd�_��u�����ق��������킯�ł��B
�Ƃ��āA�w�����`���܂����A�m���ɍ��Z���ɑ��Ă͌`���s�ςƂ������Ă��o���Ĕ[�������Ă��܂��A���p�E���p�ɏd�_��u�����ق��������킯�ł��B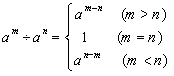 �C
�C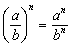
|
�R�D(ab)p=apbp�̏ؖ� �@�K���Ȏ���q���l����ƁA 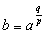 �Ƃ����܂��B �Ƃ����܂��B�@�@�@(����)= 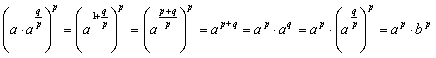 =(�E��) =(�E��)
|
�w�����֗��ȑΐ��Ƃ����������ɓ���Ă���A�������͂��̊Ԃɂ��w���@���R�͎g��Ȃ��Ȃ��Ă��܂��Ă���̂ł��B
�Ƃ���ŁA�w���ɂ͑ΐ��ȊO�ɂ�����ʂ̓ǂݑւ��ł��镶�@�\��������܂��B
�Ⴆ��
�@�@�@8=23�́A3=log28
�Ƒΐ��\������܂����A��Q�����Ƃ��āA
�@�@�@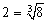
�ƕ\�����Ƃ��ł��܂��Bm���Q�ȏ�̎��R���̏ꍇ�A���̂R�͂��ׂ�m�Cn�Ca�̓����W��\���Ă��邱�ƂɂȂ�܂��B
�@�@�@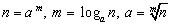
���ɁA�R�߂̗ݏ捪�ׂ͂���ɊW���鎮�ł����A���̎��̎g�������w���E�ΐ��ɊԂɂ����Ĕ����ȊW�ɂ���A�`���s�ς̌�������L���w���ւ̊g���ɍ��킹�ēs���̂����悤�ɒ�`���ꂽ�悤�Ȉ�ۂ��w���E�ΐ��P���ł͎Ă��܂��܂��B����ɁA�g�������������i�K�ł́u�̂ċ����Ă��܂��v�X��������܂����A�Ɨ���������Ƃ��ė�������K�v�����������Ă��܂��B���̂�������Z�ł��̂��ƂɐG��邱�Ƃ��ł���Ǝv���܂��B
�Ō�ɁA�{���̏I���ŁA�搶���܂ȂԂɓ������������t��ނ͂ǂ��~�߂��̂ł��傤���B
����̏���Z�ł������Ƃ��āA�����q�Ƃ܂ȂԂ̔����ȊW��D������Ă��܂��B
�V�R�{�P�Ȃ̂��A�݊��Ȃ̂��A�Ƃ�Ȃ̂��A�ǂ����߂��Ă�����������Ȃ��܂ȂԂ̎p���ɑ��āA�搶���A������������o���Ă��܂����B
���w���@���͒�=1�̏ꍇ���������܂����A�������ΐ��@���ł͒ꁂ�P�ł��̂ŁA���̏ꍇ�ɑ��Ă̓��l���ƂȂ�܂��B
�������I���Ɂu�������v���u�������v��ǂ�ł��܂����A����͉����̖{�ɏ����Ă������悤�ȋC�����܂��B�o�W�����T���܂���ł����B�Q�l�����Ƃ��čڂ��邱�Ƃ��ł����A�\����܂���B