

ex) 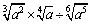 を簡単にせよ を簡単にせよ
|
<よしお> の形に直して,指数法則を使って計算する問題だね.
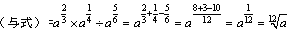
とすればいいだろ.
<かず子>うーん.やっぱりそういう解答になってしまうよね.
<まなぶ>なにか問題でもあるのかい.
<かず子>大したことじゃないのかもしれないけど,次のようにしたらどうかなって考えたの.
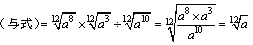
<よしお>指数の形にしないで,n乗根のままで計算するってことだね.
<かず子>そう.私ね,累乗根の公式の復習をしていたら,
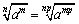
この公式を使う場面がずいぶん少ないと感じたの.だからこの公式を活かせないかと思っていたら,先ほどの問題で使えたのよね.
<まなぶ>確かにこの公式を使うことってめったにないよな.授業ではこのあとに指数法則を学ぶから,たいていの問題は指数計算でできてしまい,必要なくなってしまう.
<よしお>でも,この公式の方が,2乗根の根号計算の流れと同じだから解き易いかもしれないね.
<かず子>さすが,よしおは誰かさんとは違って良く分かっていらっしゃる.私は,累乗根で表現されている値は指数の形にわざわざ直す必要はないと思うのよね.以前,「指数と対数って同じ数を表しているのでは」ということで議論したことがあったでしょ.累乗根って指数法則がでてきた段階で使い捨てられてしまうように印象があるけど,私には,
「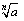 はn乗するとaになる数」
はn乗するとaになる数」
とそのまま読めるから,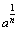 よりずっと親しみやすいように思えるのね.
よりずっと親しみやすいように思えるのね.
例えば,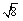 は
は 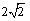 であり,これを,
であり,これを,
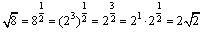
こんな風に計算する人はいないでしょ.
<よしお>そうだね.先ほどの公式 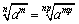 も,
も,
「n乗するとamになる数は,np乗するとamp乗になる」
と,自然に読めてしまうから,同じように考えた方がスムーズに計算ができるね.
<かず子>そうそう,それがいいたかったのよ.n:m=np:mpと比でみることができるじゃない.
<まなぶ>まあね.指数法則で考えれば,
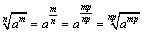
なんだから,比になるのは当たり前だけどな.
<かず子>まったくもう,面白くない男ね.だいたいまなぶが言ってる指数法則は,もともと 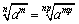 のような累乗根の性質から導かれているものじゃない.本末転倒よ.わたしがいいたいのは,例えば,
のような累乗根の性質から導かれているものじゃない.本末転倒よ.わたしがいいたいのは,例えば,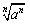 は,n:n=1:1とみると,aに等しいといったことがとても分かりやすくなるってことよ.
は,n:n=1:1とみると,aに等しいといったことがとても分かりやすくなるってことよ.
<よしお> 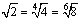 といった変形も容易にできるしね.次のように大小比較の問題も扱いやすいと思う.
といった変形も容易にできるしね.次のように大小比較の問題も扱いやすいと思う.
ex)次の各数の大小を比較せよ.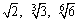
|
<まなぶ>両辺を6乗すると簡単に比較できるってやつだな.
<かず子>そうだけど,その方法だと,累乗したものの大小比較をするわけだから,最後に,もとの数でも同じ大小関係がいえてることを確認しなけりゃならないでしょ.でも
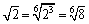 ,
,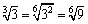
とすると,
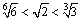
がすぐにいえるわ.どう,簡単じゃない.
<先 生>何をそんなに難しい顔をしてるんだい.
<まなぶ>わっ!,びっくりした.先生って休み時間にも現れるんですね.
<先 生>人を幽霊と一緒みたいな言い方するなよ.どれどれ……,なるほど,面白いね.
<かず子>でしょ,でしょ.なのに,まなぶったらこの面白みが分からないんだから.
<先 生>実は,先生も似たようなことを考えていたんだ.ただし,対数についてだけどね.
<まなぶ>そりゃあ,指数と対数は同じようなものだから,当然…,
<かず子>先生,無視して先を続けてください.
<先 生>そうだね.logaMを日本語訳すると,
「何乗するとaはMになるか?」
ということだったね.であるならその値は,
「何乗するとapはMpになるか?」
と考えてもおなじことだ.だから,
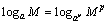
であることが分かる.これはいってみれば,底の変換公式の簡易版だね.
<まなぶ>でもそんな風に考えなくても,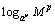 の底を a に変換するとlogaMになるのは明らかだから,わざわざ公式を作らなくても底の変換公式だけで十分じゃないですか.常日頃,先生は公式は最小限のものだけ覚えればいいっていってるし.
の底を a に変換するとlogaMになるのは明らかだから,わざわざ公式を作らなくても底の変換公式だけで十分じゃないですか.常日頃,先生は公式は最小限のものだけ覚えればいいっていってるし.
<かず子>分かってないわね.先生がいっているのは,logaMが,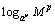 と変形できるってことよ.例えば,log23の底を4にするとしたら,
と変形できるってことよ.例えば,log23の底を4にするとしたら,
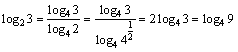
すごく面倒な印象を受けるじゃない.でも先生のいっている方法だと,
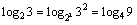
と簡単にできるわ.
<よしお> log23=log49=log827と底を累乗するならいくらでも変換できますね.
<先 生>どうだ.結構使い勝手がいいだろ.これを使えば例えば,方程式
log3x=log9(x+4)
は,底を3に統一して考えるよりも,
log9x2=log9(x+4)
とするとすぐに真数比較ができる.では,同じように3数
log427,log29,5log83
の大小比較はどうすればいいだろう.
<かず子>底を8か2に変えればいいんですね.例えば底を2にするのであれば,
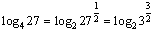 ,
,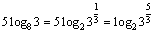
あとは指数の部分を比較するだけね.
<先 生>指数法則は便利な法則だけど,それを使ったても計算が機械的にできるというだけで,楽になるわけではない.むしろ累乗根,対数計算どらちもそのまま変形できた方が指数という垣根を通さない分,見やすく,分かりやすくなるものだ.人間だって「素」のままの人物を評価できる方がいい.指数のように底の肩に乗った飾りをみてしまうとなかなか本質には迫れないものだろ.
<まなぶ>どうも先生の最後のまとめはいつもちくちく刺さるんだよな.
<かず子>ちくちくどころか,私の胸にはぐっさり刺さったわ.