

札幌新川高等学校 中村文則
| ex)40人のクラスで、兄弟のいる生徒は28人、姉妹のいる生徒は23人いる。次の問いに答えよ。 (1) 一人っ子は何人以下か。 (2) 兄弟も姉妹もいる生徒は何人以上、何人以下か。 (3) 兄弟しかいない生徒は何人以上、何人以下か。 (4) 姉妹しかいない生徒は何人以上、何人以下か。 |
<まなぶ>うーん。なんだかよく分かりませんが。
<先 生>どこがどうわからないんだろう。
<まなぶ>その「どこ」がわからないんです。
<よしお>同感です。一般に、問題には解決のための道筋があるかと思うのですが、この問題の場合、その入口が分かりにくくて、どうアプローチしていいか見当がつきません。
<先 生>それじゃ、まずその入口から探ってみることにしようか。先生がもっているこのわら半紙を使うと実はすぐに発見できる。わら半紙をハサミで切って、各集合の人数を表すカードを作成しよう……。

さあ、できた。この3つのカードの幅はそれぞれの人数に合わせてある。
 <かず子>「生徒総数」カードの下にある点はなんでしょうか。
<かず子>「生徒総数」カードの下にある点はなんでしょうか。
<先 生>一つの▲が一人分を表しているんだ。スケールということだね。
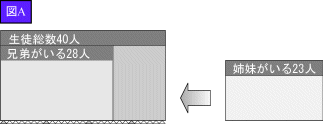
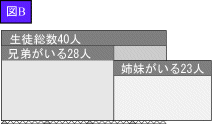
さて、ではこの3枚のカードを使って、もう一度問題を考えてみよう。 まず、「生徒総数」のカードに「兄弟」カードをこのように重ねる(図A)。さて、次に「姉妹」カードを「生徒総数」カードに右からスライドさせて差し込んでみよう。「兄弟」カードに当たったところで止めると(図B)カードがはみ出してしまうね。これはどうしてだろう。
<よしお>それは、兄弟がいる生徒の中には姉妹もいる生徒がいるということです。
 <先 生>そうだね。当然、姉妹カードは「全体総数」カードの中に含まれてなきゃおかしい訳だから、この「姉妹」カードはもっと差し込まなきゃいけないことになる。ではどれだけ差し込めばいいか、ちょっと考えてごらん。先生がゆっくりと差し込むからいいというところで「ストップ」をかけてください。
<先 生>そうだね。当然、姉妹カードは「全体総数」カードの中に含まれてなきゃおかしい訳だから、この「姉妹」カードはもっと差し込まなきゃいけないことになる。ではどれだけ差し込めばいいか、ちょっと考えてごらん。先生がゆっくりと差し込むからいいというところで「ストップ」をかけてください。
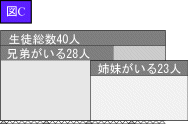 <まなぶ>ストップ!(図D)
<まなぶ>ストップ!(図D)
<先 生>ストップがかかったね。どうして、まなぶはここで止めたのかな。
<まなぶ>はい、ちょうど姉妹カードが「生徒総数」カードに収まったからです。
<よしお>でも、きっちり収まっている必要はないと思うな。
<かず子>そうよ。その状態だと、兄弟と姉妹がいる生徒で生徒全体が占められてしまうということだから、一人っ子がいなくなるわよ。クラスの中で一人っ子がひとりもいないなんて、おかしいわよ。
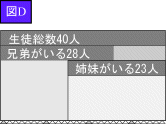 <先 生>そうだね。でもまなぶのストップをかけた位置も重要だ。この位置が、「姉妹」カードを差し込む出発ラインになっているということだ。では、このあとどれだけ「姉妹」カードを挿入できるだろうか。次はよしおが、ストップをかけてごらん。
<先 生>そうだね。でもまなぶのストップをかけた位置も重要だ。この位置が、「姉妹」カードを差し込む出発ラインになっているということだ。では、このあとどれだけ「姉妹」カードを挿入できるだろうか。次はよしおが、ストップをかけてごらん。
<よしお>ストップ(図F)
<先 生>カードはまだ左に動かすことは可能だけど、どうしてこの位置でストップなのだろうか。
<よしお>それは、この状態は姉妹カードが兄弟カードにスッポリと含まれる最初の位置だからです。あとは左に動かしても、状況は同じだと思います。
 <先 生>その通り。結局、「姉妹」カードは、図Dと図Fの間を動けるということだね。
<先 生>その通り。結局、「姉妹」カードは、図Dと図Fの間を動けるということだね。
このことが理解できれば、もう、今日の問題は解けたようなものだ。
<まなぶ>どうしてですか。
<先 生>例えば、(1)だ。一人っ子はカードではどこの部分で表されているかな。
<まなぶ>自分以外はいないということだから、「兄弟」カードでも「姉妹」カードでもない部分です。
<先 生>では、その人数は、図Dと図Fでは何人だい。
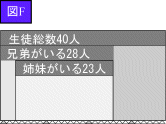 <まなぶ>はい。図Dにはいません。図Fでは、「兄弟」カード以外の部分だから、
<まなぶ>はい。図Dにはいません。図Fでは、「兄弟」カード以外の部分だから、
40−28=12(人)
だから、一人っ子は、12人以下ということか。
本当だ。できちゃった。先生、他の問題もやっていいですか。
(2)の兄弟も姉妹もいる生徒は、「兄弟」カードと「姉妹カード」が重なっている部分だから、図Fでは23人。図Dでは、えーっと、スケールの▲を数えると……、11人です。したがって、11人以上23人以下ということですね。
<かず子>まなぶ。いちいち数える必要はないわよ。図Dの場合は、「兄弟」カードと「姉妹」カードの人数を足すと51人だから、40人からオーバーしている数が重なっている値だわ。
<まなぶ>そんな計算でやってしまったら、せっかく先生がスケールを入れてくれた意味がなくなるじゃないか。口を挟まないでくれよ。次の(3)は、「兄弟」カードの中で「姉妹」カードと重なっていない部分だから、図Dでは
40−23=17人
図Fでは、
28−23=5人
です。だから、5人以上17人以下ということ。同様に、最後の(4)だけど、姉妹だけがいる部分は、「兄弟」カードと重なっていない「姉妹」カードの部分だから、図Dでは、
40−28=12人
です。図Fでは、「兄弟」カードに「姉妹」カードは含まれてしまったから該当者ゼロ。結局、
12人以下
ということです。
なんだ、この問題、意外と簡単だったんだ。
<かず子>入口が見つかってしまえば簡単ということでしょ。まなぶったら、一人じゃ道筋がみつけられず、オタオタして遭難しそうになるくせに、道が見つかったら、周りをほったらかしにしてどんどん先に登ってしまうんだから……。
<先 生>今日は最初にみんなの家族調査をしてみよう。兄弟のいる人は、手を挙げてください。えーっと、28人ですね。では、次に姉妹のいる人は……、23人ということだね。さて、そこで問題だ。このクラスの在籍数は40人だけど、いまの調査から、兄弟も姉妹もいる人、兄弟しかいない人、姉妹しかいない人、一人っ子の人数の上限、下限を求めてみよう。
と、こんなくだりになる筈でした。
そして、締めくくりは、設問の実際にいる人数を挙手させて、計算で求めた範囲の中にはいっていることを確認させて、終わり。
と、まあっ、こんな展開を考えていたわけです。ところが、ここでひとつ問題が起きました。それは、本小手技の授業の状況設定が極めて曖昧であったということです。もともと、著者の大雑把な性格を反映して、いい加減な動機から本シリーズはスタートしました。最初は、生徒名は、S君、T君といったイニシャル名であったものが、そのうちいつのまにか、「かず子」、「まなぶ」(数学をもじっただけの)と安易な名前をつけ、ボケと突っこみのキャラクターを作っていました。やがてこの2人の間をとりもつ生徒もいた方がいいだろうということで、いつのまにか「よしお」が参戦してきました。ここから3人の丁丁発止が始まるわけです。キャラクターについて整理すると、
| まなぶ……遊ぶことは好きだけど、勉強は大嫌い。性格は自己チューで、お調子もの。数学については計算は嫌いだが、意外と論理的に考えるのは好きだったりする。自由な発想はときどきみんなを驚かせる。 かず子……姉御肌のしっかり娘。何事にも前向きに努力する。まなぶのいい加減な性格にはいつも閉口している。特に、「組合せの小手技」のときに、2人の間の亀裂は大きくなった。以後、ときどき衝突する。しかし、まなぶのときおり見せる発想は評価している。 よしお……学力優秀で、数学的素養も極めて高い。問題の解決にあたっては、リーダーとして他の2人を引っ張っている。優しい性格で、かず子とまなぶが仲たがいをすることを気にしている。 |
とでもなります。
この3人と、問題提起をする先生で小手技シリーズはビミョウなバランスを保ちながら、ストーリー展開してきたのですが、実は一番大事なことを忘れていたことに本文の書き始めに気がつきました。「この3人はどんな学校いっているのだろうか」ということです。
小手技の登場人物は先生とこの3人しかいないわけですから、学校が、高等学校の1学級というには無理があります。40人中3人の発言での学習進行では余りに偏った授業ということになります。それでは、生徒数が3人しかいないどこかの僻地分校か、それとも少数制の塾か、何より、「先生」はいったいどんな人物なのか。前述したように、こういった設定はまったく無視して本シリーズはスタートしたのですが(だいたい、数実研でのアイデアの「相乗り」の一事例のつもりで軽く作ったものが、「相乗り」されないうちに、悪乗りして、エスカレートしていったのですが)、著者としては、レポートをタイピングをしているうちに、たぶん無意識に次のことを意図してしまったような気がします。
先生は、レポートを呼んでいる「あなた」を想定し、3人は、「あなた」が問題対峙の中で、葛藤し逡巡する思考の一断片を投影したもの
となります。ところが、本文のような題材設定では途端、綻びをみせてしまったわけです。
大雑把な性格故、今後、キャラクターにしろどうデフォルメしていくか著者でも予測不能ですが、よかったらお付き合いください。
そろそろ、本文の内容に戻ります。
本文のような問題の解答方法にはいくつかありますが、一般的なものは集合の性質を使った計算によるものでしょう。本文の設問は次のように集合で表すことができます。
U={生徒全体の集合},A={兄弟がいる集合},B={姉妹がいる集合}とする。
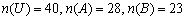 のとき、次を求めよ。
のとき、次を求めよ。
(1) 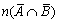
(2) 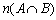
(3) 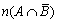
(4) 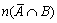
ここで例えば(1)は、
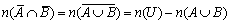
となります。また(2)は、
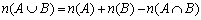
から求めらます。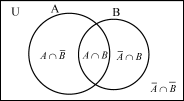 以上より、この問題のポイントは、
以上より、この問題のポイントは、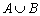 の人数を押さえることにあることが分かります。
の人数を押さえることにあることが分かります。
ここで、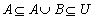 より、
より、
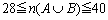
よって、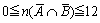
また、 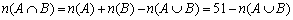 から
から
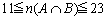
次に、 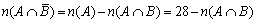 より、
より、
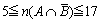
同様に、 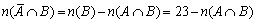 より、
より、
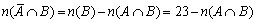
以上、求めることができました。
このように、論理的に集合算をしていけば結論は導かれますが、個数の変化の状態がまるでみえず、後味の悪い印象を残してしまいます。そこで、視覚的に変化量を捉えることができないかと思い考えた方法が本文の集合カードです。これは単にオイラー図式をカード化しただけのことですが、カードの幅を人数に対応させることで、変化量を追っていけるようにしました。
集合カードには思考的な要求はありません。ベン図の集合の張り付いた(凍りついた)イメージを揉み解し、可変性にしたということです。本文中生徒発言にある「何がわからないのか分からない」ことの要因は、集合を柔軟に動かすことができないことであり、道筋が見えなくなっているわけです。集合カードの作成を通して、「作って手に持つことで」、抽象概念から具象概念へと集合が転換したことを意味します。教材のビジュアル化は、思考発展の補助的、導入的手段にひとつであるといえるでしょう。
また、本文中、先生が、集合カードの適正配置を要求するときに、生徒に「ストップ」といわせ、止めることを要求する場面があります。私自信この手法はよく使います。例えば、定義域が変化する二次関数の最大最小問題において、指示棒を定義域に見立ててスライドさせ、最大点・最小点の変わり目にストップをいわせます。わざと動かすスピードを速めて生徒が慌てるのを喜んじゃったりしています。ここで、ストップを言わせることは、もちろんそれを言う生徒の理解を問うものですが、同時にそれを聞いている周りの生徒への確認でもあります。こういった音を通して理解することは、従来の数学の授業の中では希薄であった部分と思います。
ところで、このような視覚的、聴覚的な理解補助の手段を私は興具(教具という場合もありますが)と考えています。有形・無形を問わず、それは種種のパターンとバリエーションが予想されます。
大山斉先生が指数関数の導入に光の透過率を利用したことは記憶に新しいことです。先生はまた、プラックボックスを実際に作成し、関数のモデル授業をしてくださったこともあります。
加藤渾一先生は、三角形の五心を折り紙の中に凝縮しました。新しいオリガミクスという興具が誕生しました。
コンピュータグラフィックは時代の先端を突っ走っています。数学においては、3次元住人にはいままで見えなかった3次元オブジェクトの造形により、3Dグラフの背景を探ることができるようになり、早苗雅史先生によりShadow Lineは完成しました。
このような視覚補助に代表される興具による授業展開は、今後の数学教育においては必要不可欠になるのではないかと思います。今から20年ほど前に、MOVEなる活動を提唱したことがあります。Mathematics Of Visual Effect 訳せば、視覚補助による数学ということになりましょうか。当時の教育環境では活動に無理があったのですが、いまは「5分の教材は5分で作れる」……菅原満先生の名言……時代です。 MOVEはやっと動き出したといえます。
さて、その潮流に乗っかろうと思い、今回の小手技には、他聞に興具的な部分を織り込みました。集合カードというちっぽけな興具ですが、ここからいまひとつのシリーズを始めようかと思っています。
名前は「メイクル数学」。数学をmake upしようということです。
近いうちに、この研究会で発表できればと考えています。