札幌新川高等学校 中村文則
<まなぶ>えーっと、(初項)+(n-1)×(公差)だから、
2+(n-1)×3=3n-1
です。
<先 生> かず子、いいかな?
<かず子> はい。何か問題でもあるんですか。
<先 生> 一般項はあっている。ただその求め方がちょっと気になる。先生の質問の仕方に何か感じなかったかい。
<よしお> ……、そういえば先生は公差から先にいってましたよね。
<まなぶ> そうだ。だから、妙に計算がしにくかったんだ。等差数列は初項から一定数ずつ増えていく数列なんだから、最初に初項を考えるべきで、さっきのように出題されると計算がワンテンポ遅れてしまうよね。
<先 生> 確かに公式に適用すると、まなぶのいう通りだけど、でも等差数列で初項の値はそれほど大事なことなんだろうか。
<まなぶ> そりゃ、大事ですよ。何事も始めが肝心でしょ。
<先 生> いいこというね。じゃあ、ちょっと質問を変えよう。公差3の等差数列を一つ挙げるとしたらみんなはどんなものを考える。
<かず子> うーん、3,6,9,12,15,…… でしょうか。
<先 生> たぶん、他のみんなも同じように、初項が3である公差3の等差数列を考えたのでないだろうか。では公差が4ではどうだろう。
<よしお> 初項4の等差数列で、4,8,12,16,……となります。
<先 生> ところで、これらの数列は初項なになに公差なになにの等差数列というのではなくもっと分かり易い表現があるだろ。
<まなぶ> 倍数ということですか。
<先 生> その通り。初項3で公差3の等差数列は、3の倍数といえる。つまり、この場合、公差はどんな数の倍数かということを表している訳だ。では、そう考えると初項は何を意味することになるだろう。
<かず子> ……あのう、余りですか。
<まなぶ> どういうこと、かず子。
<かず子> 等差数列は、nの一次式で表されるじゃないですか。例えば、4n+3といったら、4で割ったら余りが3の等差数列とみればいいんです。
<まなぶ> なるほど。でも一般項が4n+10なんて等差数列も考えられるよ。そしたら余りは10になってしまうじゃないか。
<先 生> まなぶのいう通りだね。4n+3の場合も、n=1とすると、初項は7だから、これも余りとはいえないね。でもかず子の発想は間違いじゃない。余りを倍数の値からどれだけ離れているかというズレと解釈すると、等差数列でも初項は倍数のズレを表しているとみればいいんだ。そうすると4n+3や4n+10は、倍数4nに対して、それぞれ4、10右方向に数がズレたというように考えられる。
<よしお> そうか。だから最初に公差なんですね。公差で倍数が決まって初項でズレるというわけか。
<先 生> そうだね。等差数列は「最初に公差ありき」なんだ。では、公差7で初項4の等差数列の一般項はどうみればいいかな。
<まなぶ> はい。まず7の倍数だから、7n。そして初項が4になるようにズラすと……、7n−3が一般項になります。
<先 生> 正解だ。では、演習問題を1つ。
| ex1) 第12項が30、第27項が60である等差数列{an}の一般項を求めよ。 |
<かず子> an=a+(n-1)d とすると、a12=30,a27=60 ですから、
a+11d=30, a+26d=60
あとはこれを解けばいいわ。
<先 生> おいおい、それじゃ「初めに公差ありき」の演習にならないよ。もとの等差数列の一般項の公式に戻ってしまっている。
<よしお> では先生、どうすればいいんでしょうか。
<先 生> 数列の大事な性質をおさらいしておこう。 「数列の並びから適当な部分を選んでも、もとの数列の性質は引き継がれる」ということだ。例えば、等差数列のどの部分を切り取っても公差が同じである等差数列になっているというわけだ。
<よしお> ということはこの問題も、第12項と第27項を切り取ってひとつの等差数列を考えろということですね。
<まなぶ> そうか。じゃあ、第12項が初項で、第27項がえーっと、第16項で、そして……、先生、僕には却って難しくなってしまったような気がするんですけど。
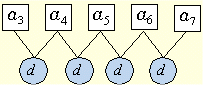 <先 生>もう一度言うけど、 「初めに公差ありき」だ。初項を最初に考えてしまうと本末転倒になってしまう。大事なことは、公差をどれだけ加えていったかということなんだ。右図をみてみよう。第3項から第7項の間に加えられた公差は7−3=4つだね。これは、a3を初項と考えれば、
<先 生>もう一度言うけど、 「初めに公差ありき」だ。初項を最初に考えてしまうと本末転倒になってしまう。大事なことは、公差をどれだけ加えていったかということなんだ。右図をみてみよう。第3項から第7項の間に加えられた公差は7−3=4つだね。これは、a3を初項と考えれば、
a3+(7-3)d=a7
ということだ。これから、
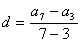
これを、anからanまでの等差数列にしても同じことだろ。
 <かず子> an=am+(n-m)d
<かず子> an=am+(n-m)d
ということですね。そうすると、これから  となります。
となります。
<先 生> ではこれを利用して先ほどの問題を解いてごらん。
<まなぶ> 公差をdとすると、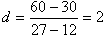 。すると2の倍数だから2n、あとは初項を求めて……?、あれ、どうすればいいんだろう。
。すると2の倍数だから2n、あとは初項を求めて……?、あれ、どうすればいいんだろう。
<かず子> まなぶ、第12項目を初項と考えるといいんじゃないの。
<まなぶ> そうか。そうすると、n=12を代入して24、これが30になるようにズラすといいわけだから、一般項は、2n+6 です。なるほど。こうやって等差数列をみるとなんだかぐっと数列が身近になったような気がしますね。
| ex2) 数列{an}の初項から第n項までの和が、 Sn=3n2+4n で与えられるとき、数列{an}の一般項を求めよ。 |
<よしお> これは簡単ですね。公式
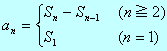
に当てはめればOKです。
<先 生>一般項から和を求めることは難しいけれど、その逆は簡単によしおのいった公式から、どんな数列{an}に対しても求められるんだったよね。でも、この問題の場合、和はnの定数項のない一次式で表されているね。この場合、求める{an}はどんな数列だろう。
<かず子>はい。等差数列です。
<先 生> であれば、前回の結論から何を求めればいいかというと……
<まなぶ> 初めに公差ありきですね。
<先 生> そうだね。では、和が Sn=pn2+qn なら、等差数列の公差はなにかということだが、それは、等差数列の和の公式をみるといい。
<まなぶ> (和)=1/2・(項数)(初項+末項) でしたよね。
<先 生> ガウス少年の発想を再現すると、等差数列の和は、最初と最後の項の平均に項数を掛けたものだったね。すなわち、等差数列の一般項を an=dn+e とするとその和は、n/2・(初項+dn+e) ということだ。これからpとdの関係が簡単に導かれる。
<かず子>d=2pですね。そうか、dは公差だから、和を表しているnの2次式の2次の項の係数を2倍したものが公差ということですね。
<よしお> なんだ。すると僕が計算しようとしていたことは無駄なことだったんだ。問題の2次の項の係数は3だから、公差は6。したがって6の倍数だから6n。あとは初項ですね。
<まなぶ> それはよしおのいってた a1=S1 が使える。S1=3+4=7 だからズレを考えると、an=6n+1 となります。
<先 生> よしおの述べた公式は、任意の数列の和からその一般項を求めるためのものなんだ。等差数列という既に和の公式が与えられているものに対してまで使う必要はない。等差数列では常に「初めは公差ありき」ってことだね。
| ex3) 第3項が−40の等差数列において、第6項から第16項までの和が0であるとき、この数列の一般項を求め、初項から第何項までの和が最小になるか調べよ。 |
この問題は、機械的に計算すれば求められる。どうすればいい。
<よしお> 問題文を式化していくと。
a3=-40,S16-S5=0
あとは、初項をa、公差をdとして、aとdの関係式を2つ作ればいいと思います。
<先 生>そうだね。それを初めに公差ありきで求めてみよう。まず、「第6項から第16項までの和が0」というのはどういう状態なんだろうか。
<かず子> 第3項が負の値だから、条件を満たすためには公差は正の値をとり、項の値は増えていって、6項と16項の間の項で、正負が相殺されて0になるのだと思います。
<先 生>素晴らしい。ちょっと確認してみようか。「等差数列はどこで切っても等差数列」であることを使おう。第6項、第16項の値をそれぞれa,bとして、関係式を求めるとどうなるだろう。
<まなぶ>第6項を初項と考えると、第16項までの項数は11だから、和の公式から、
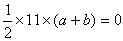
<先 生>これからb=-a なる関係が得られるね。これは、第6項と第16項は絶対値が等しい異符号の値ということだ。すると等差数列であることより第7項と第15項、第8項と第14項などもみな同じ関係のpairになるわけだ。ところで、項数は11だったから、pairにならない項がひとつある。それは第何項だろう。
<よしお>第6項と第16項の平均である第11項だと思います。
<先 生>ではその第11項の値はなんだろう。
<かず子>pairが相殺されて、かつ和が0なんだから、singleの第11項は0でなくちゃおかしいわ。
<先 生>そう、その通り。結局この問題は、第3項が−40で、第11項が0となる等差数列の一般項を求めろということだ。
<まなぶ> そうすると、初めに公差ありきだから、
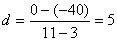
一般項は5n+…で、第3項が−40だから、5n−55となります。
<先 生> では後半の最小値を計算してごらん。
<よしお> 計算の必要はないと思います。だって、第11項が0なんだから、第11項かまたは、その前の第10項までの和が最小値であることは明らかです。
<先 生> OK!。では、もう1題。
| ex4) 第3項が6の等差数列がある。初項から第6項までの和と、初項から第14項までの和が等しいとき、この数列の一般項を求めよ。また、第n項から第(n+7)項までの和をTnとするとき、|Tn|の最小値とそのときのnの値を求めよ。 |
もちろん、この問題も式化して解くことが可能だけれども、条件の意味から進めてみよう。
<かず子> 第6項までの和と、第14項までの和が等しいということは、第7項めから第14項までの和は影響していないということだから0ということだと思います。
<まなぶ> そうか。そうするとこの問題は先ほどのex3)とまったく同じってことだ。第7項と第14項の平均の項が0であればいいから、足して2で割ると……、あれっ、先生、分数になっちゃいます。
<先 生>そうだね。第7項から第14項までの項数は8項。すなわち、すべての項でpairが作られてしまうんだ。そうすると先ほどのような考え方はできなくなってしまうね。なにかいい方法はないだろうか。
<よしお>先生、取りあえず平均を求めると、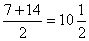 。だから、第10項と第11項がpairになることが分かるから、これから第3項のpairを探せばいいのではないでしょうか。
。だから、第10項と第11項がpairになることが分かるから、これから第3項のpairを探せばいいのではないでしょうか。
<先 生>うん。いい考えだ。第9項と第12項、第8項と第13項っていうように数えていけばいい。あるいは、pairを第m項とすれば、
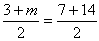
を満たすから、m=18 と求められる。さあ、あとはやってご覧。
<かず子> 第3項が6、第18項が−6だから、公差dは、
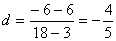
となります。したがって、 でn=3のとき、6となるズレαを見つけると、一般項は 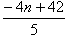 となります。
となります。
<先 生>さあ、ラストだ。後半を解いてみよう。これも「どこで切っても等差数列」ってことを利用し、第n項を初項と考えると、第(n+7)項は8項目になる。したがって
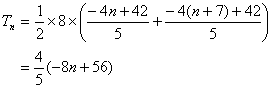
これから、|Tn|≧0であることより、|-8n+56|≧0 よって、n=7で最小値0となることが分かる。
でも、みんなはもうこんな計算をしなくても答えは出せるよな。まなぶ、代表していってご覧。
<まなぶ>はい。項数が8項だから、相殺して0になる4つのpairを作ればいいだけです。第10項と第11項が一番近いpairだから、第10項から3つ前の項が答えになります。すなわち、第7項です。
<先 生>正解だ。結局、等差数列の問題は、最後まで公差が絡んでいたのが分かるね。「終りも公差ありき」ってことだ。
| ex) an=3n+5,bn=4n-1 とするとき、数列 {an},{bn} に共通に含まれる項で、1000以下のものの和を求めよ。 |
これは、ズレを無視すると、3の倍数と4の倍数ということになりますから、共通項は、3と4の最小公倍数である12の倍数ということになります。あとは、12nのズレを見つけて、その和を求めればいいわけです。
次に「等差数列はどこで切っても公差が同じ等差数列」という考え方は、とくに群数列では欠かすことのできないものでしょう。そしてここにも「初めに公差ありき」が顔を覗かせます。解決の糸口は、等差数列では常に公差なのです。ところで後半は、応用問題へのトライとなり、小手技という内容からは少しはずれてしまいました。(最近、だんだんと「こてわざ」というより、「こったわざ」になる傾向が顕著になってきています。)。
これを小手技風にアレンジすると、次のようになるでしょうか。
まず、等差数列がnの1次式で表されるということに注目しましょう。すると、an=pn+q とみれば、(nが自然数であるということを無視すると)直線の方程式を表しています。すると、公差pは、直線の傾きと考えることが可能になるわけです。
そうするとex2)の第12項が30、第27項が60の等差数列の一般項は、2点(12,30),(27,60)を通る直線の方程式を求めれぱいいわけです。
したがって、 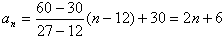
となります。
ex3)も同様です。さらにex4)ですが、まず、第3項が6より、点(3,6)を考えます。次に第7項と第14項の平均が0ということから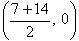 なる点を通る直線を求めればいいことになります。これから、
なる点を通る直線を求めればいいことになります。これから、
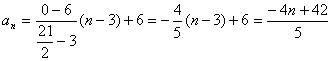 が得られるわけです。
が得られるわけです。
なお、「初めに公差ありき」はもちろん等比数列にあっても同様です。「初めに公比ありき」です。その典型は隣接2項漸化式でしょう。
an=2an+3
を満たす数列 {an} の一般項は、平衡値によりズレを修正します。では何がずれていたのかというと、
an=2an
であることは明白でしょう。これから、 {an} は公比2の等比数列が少しずれたと解釈できます。したがって、
an=p2n+q
とおけます。さて、あとはp,qの値ですが、第1項、第2項の値を代入すれば簡単に求められるわけです。
この解法は隣接3項漸化式でも裏技として紹介されるものです。