丂惓尫丒梋尫掕棟偺斵曽偵偁傞傕偺
亙愭 惗亜嶰妏宍傪寛掕偡傞偵偼丄
丂丂丂嘆俁曈丂丂嘇俀曈偲娫偺妏丂丂嘊侾曈偲俀妏
偑梌偊傜傟偰偄傟偽偄偄傫偩偭偨傛偹丅崱擔偼嘊偺応崌偵偮偄偰丄嶰妏宍傪夝偄偰傒傛偆丅
|
倕倶乯師偺嶰妏宍傪夝偗丅 丂丂(1)丂a=2丆B=60亱丆C=75亱丂丂(2)丂a=2丆B=60亱丆C=45亱 |
亙愭 惗亜傑偢(1)偱偡丅偝偁丄僲乕僩偵夝摎傪嶌偭偰偛棗乧乧丄偱偼丄傛偟偍丄偳偆側偭偨丅
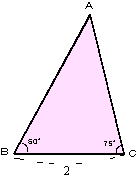 亙傛偟偍亜偼偄丄傑偢丄A+B+C=180亱傛傝丄A=45亱偱偡丅偙偙偱丄曈俛俠偲懳妏俙偑暘偐偭偰傑偡偐傜惓尫掕棟傛傝丄
亙傛偟偍亜偼偄丄傑偢丄A+B+C=180亱傛傝丄A=45亱偱偡丅偙偙偱丄曈俛俠偲懳妏俙偑暘偐偭偰傑偡偐傜惓尫掕棟傛傝丄
丂丂丂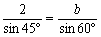 丂丂亪丂丂
丂丂亪丂丂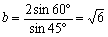
丂傑偨丄戞侾梋尫掕棟傛傝丄
丂丂丂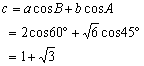
亙愭丂惗亜偱偼丄(2)傪傑側傇丄夝偄偰偛傜傫丅
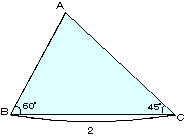 亙傑側傇亜(1)偲摨偠傛偆偵丄嶰妏宍偺撪妏偺榓偼180亱偱偡偐傜丄
亙傑側傇亜(1)偲摨偠傛偆偵丄嶰妏宍偺撪妏偺榓偼180亱偱偡偐傜丄
丂丂丂A=180亱亅(60亱+45亱)=75亱丅
丂師偵丄惓尫掕棟傪巊偭偰丄
丂丂丂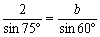
丂傛偭偰丄b=乧丂偁傟丠丅愭惗丄媮傔傜傟傑偣傫丅
亙愭丂惗亜偦偆偩偹丅75亱偺嶰妏斾偑暘偐傜側偄偐傜惓尫掕棟偼巊偊偦偆偵側偄偹丅
丂偱偼丄偳偆偡傟偽偄偄偩傠偆丅
亙惗丂搆亜丂乧乧乧丠
亙愭丂惗亜丂偦傟偱偼丄傕偆堦搙嶰妏宍偺夝朄傪惍棟偟偰傒傛偆丅嶰妏宍傪夝偔偨傔偺傾僀僥儉偼丄惓尫掕棟偲俁偮偺梋尫掕棟偟偐側偐偭偨傛偹丅梋尫掕棟偵偮偄偰偼丄俀曈偲俀偮偺妏偑暘偐偭偰偄傟偽戞侾丅俀曈偲侾偮偺妏偺偲偒偼戞俀丅偦偟偰丄俁曈偑暘偐偭偰偄傟偽戞俁梋尫掕棟乮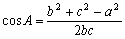 偺傕偺傪彑庤偵戞俁偲柦柤偟偰偄傑偡乯傪巊偆傫偩偭偨傛偹丅俀偮埲忋偺曈偵挿偝偑暘偐偭偰偄側偗傟偽側傜側偄偲偄偆偙偲偱偡丅崱偺栤戣偺応崌丄暘偐偭偰偄傞嶰妏宍偺梫慺偼丄侾曈偲俁偮偺妏偩偐傜梋尫掕棟偼偳偆傗傜巊偊偦偆偵側偄丅偩偐傜偲偄偭偰丄傑側傇偑傗偭偨傛偆偵惓尫掕棟傕柍棟偩偟丅敧曽嵡偱偡偹丅偳偆偡傟偽丄偄偄偱偟傚偆丅偦傟偧傟偺掕棟偱偼懷偵挿偟僞僗僉偵抁偟偩偟乧乧
偺傕偺傪彑庤偵戞俁偲柦柤偟偰偄傑偡乯傪巊偆傫偩偭偨傛偹丅俀偮埲忋偺曈偵挿偝偑暘偐偭偰偄側偗傟偽側傜側偄偲偄偆偙偲偱偡丅崱偺栤戣偺応崌丄暘偐偭偰偄傞嶰妏宍偺梫慺偼丄侾曈偲俁偮偺妏偩偐傜梋尫掕棟偼偳偆傗傜巊偊偦偆偵側偄丅偩偐傜偲偄偭偰丄傑側傇偑傗偭偨傛偆偵惓尫掕棟傕柍棟偩偟丅敧曽嵡偱偡偹丅偳偆偡傟偽丄偄偄偱偟傚偆丅偦傟偧傟偺掕棟偱偼懷偵挿偟僞僗僉偵抁偟偩偟乧乧
亙傑側傇亜愭惗丄掕棟傪崌傢偣傞栿偵偼偄偐側偄傫偱偡偐丅
亙愭 惗亜偳偆偄偆偙偲偩偄丅
亙傑側傇亜偦傟偧傟偺掕棟偱扨撈偵媮傔傜傟側偄偺側傜丄偦偺偆堦抳抍寢偭偰傗偮偱丄側傫偱傕傒傫側偱嫤椡偡傟偽偆傑偔夝寛偟傑偡傛偹丅
亙愭丂惗亜偆傫丄慺惏傜偟偄巔惃偱偡偹丅偦傟偱偼丄偦傟偧傟偺掕棟偺嫤椡偱偒傞晹暘傪扵偟偰傒傛偆丅傑偢偼丄惓尫掕棟偩丅惓尫掕棟偺恾宍揑側堄枴偼壗偩偭偨傠偆丄偐偢巕丅
亙偐偢巕亜嶰妏宍偺曈偲偦偺懳妏偺惓尫偺斾偑摍偟偄偲偄偆偙偲偱偡丅
亙愭丂惗亜偱偼丄偦偺斾偺抣偼丅
亙偐偢巕亜偼偄丄嶰妏宍偺奜愙墌偺捈宎偱偡丅
亙愭丂惗亜偦偆偩偹丅偲偙傠偱丄偄傑栤戣偱梌偊傜傟偰偄傞妏搙偺偆偪寁嶼偱媮傔傜傟傞傕偺偼丄
丂丂丂B=60亱丆C=45亱
偱偡偹丅偲偙傠偑丄偳偪傜傕懳曈偺挿偝偑暘偐傜側偄偐傜丄惓尫掕棟偼巊偊側偐偭偨偺偩偗傟偳丄偦偺斾偺抣偑奜愙墌偺敿宎偲偄偆偙偲偑暘偐偭偰偄傟偽丄
丂丂丂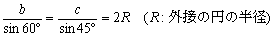
傛傝丄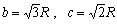
偲昞偣傑偡丅偳偆偩傠偆丅b丆c偺抣偑偪傚偭偲尒偊偰偒偨偹丅偝偰丄師偼梋尫掕棟偺弌斣偩丅偝偁丄偳偆巊偭偨傜偄偄偩傠偆偐丅
亙偐偢巕亜俁曈偺挿偝偲丄侾偮偺妏偑暘偐偭偨偙偲偵側傝傑偡偐傜丄戞俀梋尫掕棟丂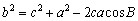 偵戙擖偟偰丄
偵戙擖偟偰丄
丂丂丂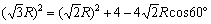
傪夝偄偰R傪媮傔傟偽偄偄偲巚偄傑偡丅
亙傑側傇亜偱傕丄妏偼俀偮偺抣偑暘偐偭偰偄傞偐傜戞侾梋尫掕棟偺曽偑偄偄偺偱偼側偄偱偟傚偆偐丅
亙愭丂惗亜傗偭偰傒傛偆丅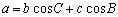 偵戙擖偟偰偛傜傫丅
偵戙擖偟偰偛傜傫丅
亙偐偢巕亜丂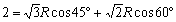 傛傝丄
傛傝丄
丂丂丂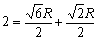 丂亪丂
丂亪丂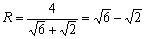
亙愭丂惗亜偟偨偑偭偰丄
丂丂丂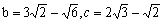
偲側傞丅傑側傇偑偄偭偨傛偆偵侾偮偺掕棟偱夝寛偱偒側偄偙偲偱傕丄屳偄偵曗偄嫤椡偟偰偄偗偽巺岥偑傒偊偰偔傞傫偱偡偹丅
俶倧倲倕乯
丂惓尫掕棟亄梋尫掕棟亖壛朄掕棟丠
丂倕倶乯偺夝朄偼丄杮暥埲奜偵傕偄傠偄傠峫偊傜傟傑偡丅侾斣埨堈側曽朄偼丄
丂丂丂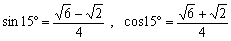
傪妎偊偰偟傑偆偙偲偱偡丅偙傟偐傜丄
丂丂丂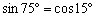 偐傜丄惓尫掕棟傛傝丄
偐傜丄惓尫掕棟傛傝丄
丂丂丂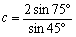
傪媮傔傟偽傛偄傢偗偱偡丅偙偺傛偆偵媮傔傜傟傞棟桼偼丄戙悢揑偵夝偔偙偲偺偱偒傞嶰妏宍偑嬌傔偰尷掕偝傟偰偄傞偙偲偑攚宨偵偁傝傑偡丅偟偨偑偄婔壗揑偵偙偺偙偲傪棙梡偡傞偲丄(1)丄(2)偲傕偵俀偮偺捈妏嶰妏宍偵暘妱偟丄偦偺曈偺斾傪峫偊傞偙偲偱媮傔傞偙偲傕壜擻偲側傝傑偡丅
(1)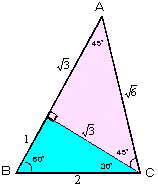 | (2)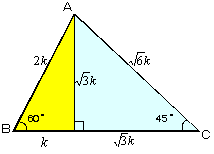 | 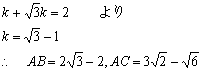 |
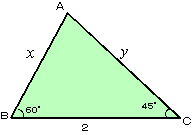 丂傑偨丄戞俀梋尫掕棟傪巊偆偲師偺傛偆側夝摎傕峫偊傜傟傞偱偟傚偆丅
丂傑偨丄戞俀梋尫掕棟傪巊偆偲師偺傛偆側夝摎傕峫偊傜傟傞偱偟傚偆丅
AB=x丆CA=y偲偍偔偲丄
丂丂丂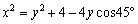 丂丂乧乧(*)
丂丂乧乧(*)
丂丂丂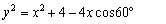
丂丂丂丂亪丂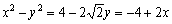
丂偙傟偐傜丄x丆y偑媮傔傜傟傑偡丅
丂偙傟偵懳偟偰杮暥偺夝摎偱偡偑丄嶰妏宍偺梫慺偲偟偰丄俀偮偺妏(俁偮偺妏)偲侾偮偺曈偺挿偝偑梌偊傜傟偰偄傞偲偒丄
丂丂丂俁偮偺妏偱宍偑偒傑傝丄侾偮偺曈偱戝偒偝偑寛傑傞
偙偲偐傜慻棫偰偰偄傑偡丅嶰妏宍偺戝偒偝傪寛掕偡傞偺偼丄嶰妏宍偺奜愙墌偺敿宎偱偡偐傜丄偙偺偙偲傪棙梡偡傞偲丄師偺夝摎偑峫偊傜傟傑偡丅
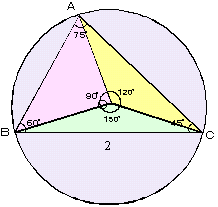 丂塃恾偺傛偆偵丄
丂塃恾偺傛偆偵丄
丂丂丂乵墌廃妏偺戝偒偝亖俀亊拞怱妏偺戝偒偝乶
偱偡偐傜丄奜愙墌偺敿宎傪俼偲偟丄仮俷俛俠偵戞俀梋尫掕棟傪梡偄傞偲丄
丂丂丂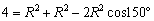
丂丂丂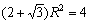 丂丂
丂丂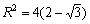
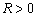 傛傝丄
傛傝丄
丂丂丂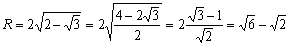
丂偙傟偐傜丄奺曈偺挿偝偑媮傑傝傑偡丅
丂偙傟傪杮暥偱偼丄惓尫掕棟傪巊偭偰奺曈偺挿偝傪奜愙墌偺敿宎偱昞尰偡傞偙偲偱戝偒偝傪寛傔偰偄傑偡丅
丂偦偟偰丄奜愙墌偺敿宎傪寛掕偡傞偨傔偵丄戞侾梋尫掕棟傪巊偭偰偄傞偺偱偡偑丄偙偺戞侾梋尫掕棟偵偮偄偰丄傕偭偲怗傟偨偐偭偨偺偑幚偼杮暥偺庯巪側偺偱偡丅
丂戞侾梋尫掕棟偼丄嫵壢彂偱偼壗屘偐徣棯偝傟傞偙偲偑懡偔乮怗傟偰偁偭偰傕栤偄偺栤戣掱搙乯丄戞俀梋尫掕棟偑戝庤傪怳偭偰巻柺傪忺偭偰偄傑偡丅壗屘偱偟傚偆丅戞侾乧偲偁傞偔傜偄偱偡偐傜丄base偼偙偪傜偱偁傞傋偒偼偢側偺偱偡丅
丂懡暘丄偦偺棟桼偼戞侾梋尫掕棟偼丄俀偮偺妏(俁偮偺妏)偲俀偮偺曈偑梌偊傜傟偨偲偒偵巊偊傞掕棟偱偁傝丄嶰妏宍偺寛掕忦審偺俁梫慺(椺偊偽(A丆b丆c)丆(A丆B丆c)丆(a丆b丆c))偵斾傋偰梫慺悢偑懡偡偓傞偨傔偱偼側偄偐偲巚傢傟傑偡丅偟偐偟丄嶰妏宍傪夝偔夁掱偺拞偱偼丄戞俀梋尫掕棟傪巊偭偰(*)偺傛偆偵柍棟偟偰俀師曽掱幃傪嶌傞偺偱偼側偔丄梫慺偑妋掕偟偰憹偊偰偄偔拞偱帺慠偵戞侾梋尫掕棟偑巊傢傟傞傋偒偱偼側偄偺偱偟傚偆偐丅
丂偦偟偰丄偦傟埲忋偵丄惓尫掕棟偲梋尫掕棟乮傕偪傠傫戞侾乯偺慻崌偣偺拞偱尒偊塀傟偟偰偄傞偁偺掕棟偺懚嵼偑婥偵側傞偺偱偡丅
丂嬶懱揑偵扵偭偰傒傑偟傚偆丅
杮暥偺傛偆偵丄惓尫掕棟傪巊偭偰曈偺挿偝傪奜愙墌偺敿宎俼偱昞尰偡傞偲丄
丂丂丂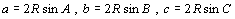
偙傟傪戞侾梋尫掕棟丄
丂丂丂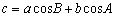
偵戙擖偟傑偡丅
丂丂丂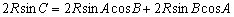
丂丂丂亪丂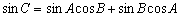
偑惉棫偟傑偡丅
丂偙偙偱丄仮俙俛俠偵偍偄偰偼丄A+B+C=180亱偱偡偐傜丄
丂丂丂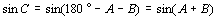
偲側傞偙偲偐傜丄
丂
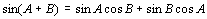 丂丂乧乧嘆 丂丂乧乧嘆
|
丂摨條偵摼傜傟傞丄
丂丂丂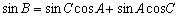
偵懳偟偰丄C=180亱亅A亅B傪戙擖偡傞偲丄
丂丂丂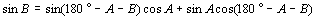
丂丂丂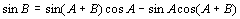
丂丂丂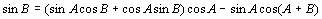
丂丂丂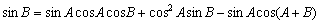
丂丂丂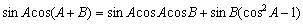
丂丂丂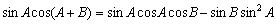
丂丂0亱亙A亙90亱傛傝丄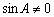 偱偡偐傜丄
偱偡偐傜丄
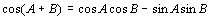 丂丂乧乧嘇 丂丂乧乧嘇
|
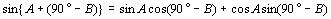
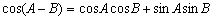 丂丂乧乧嘊 丂丂乧乧嘊
|
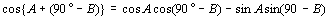 傛傝丄
傛傝丄
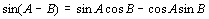 丂丂乧乧嘋 丂丂乧乧嘋
|
丂偝傜偵丄
丂(A丆B)=(0亱丆0亱)丆(0亱丆90亱)丆(90亱丆0亱)丆(90亱丆90亱)
偺偲偒丄壛朄掕棟偑惉棫偡傞偺偼柧傜偐偱偁傝丄堦斒妏俙丆俛偵懳偟偰傕丄
丂丂丂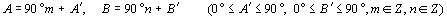
偲偍偗偽娙扨偵偦偺惉棫傪徹柧偱偒傑偡丅
丂寢嬊丄惓尫掕棟偲梋尫掕棟偺梈崌偺壥偰偵偼壛朄掕棟偑戝偒偔墶偨傢偭偰偄偨偲偄偆偙偲偱偡丅
丂峫偊偰傒傟偽丄嶰妏宍偺夝朄偺夁掱偺拞偱丄15亱傗75亱偺嶰妏斾偺抣偑媮傑偭偰偟傑偆偙偲偼傛偔偁傞傢偗偱丄偙傟傜偺妏偼壛朄掕棟傪巊偭偰杮棃媮傔傜傟傞傢偗偱偡偐傜丄惓尫丒梋尫掕棟偼壛朄掕棟揑惈幙傪娷傒傕偭偰偄傞偙偲偑埫帵偝傟偰偄偨傢偗偱偡丅
偦偟偰丄偙傟偼戞侾梋尫掕棟偐傜摼傜傟傞傕偺偱偁傝丄戞俀梋尫掕棟偱偼丄嶰妏斾偳傑傝偺恾宍偺寁検偱廔偭偰偟傑偆偺偱偡丅傛偔丄嶰妏斾偲嶰妏娭悢偺巜摫偵娭偟偰偼丄乽棏偑愭偐寋偑愭偐乿榑憟偑偍偒傑偡偑丄戞侾梋尫掕棟傪key-word偲偡傞偲僗儉乕僘側棳傟偺巜摫偺慻棫偰偑峫偊傜傟傞偺偱偼側偄偱偟傚偆偐丅