

① a≧0,b≧0のとき、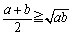 等号成立はa=b (相加相乗平均の関係) 等号成立はa=b (相加相乗平均の関係)② (a2+b2)(x2+y2)≧(ax+by)2 等号成立は、a:b=x:y (コーシーの不等式) ③ x2+y2+z2≧xy+yz+zx 等号成立は、x=y=z |
なんて不等式だったけど、ところでこの中で一番エライ不等式ってなんだと思う。
<まなぶ>一番エライ?ですか。意味がよく分かりませんが。
<先 生>例えば、①を使うことで、②の不等式がでてくれば、②は①の特殊なケース、あるいは①は②の発展型とみることができるだろ。このとき、①は②よりエライということにするんだ。
<よしお>僕は、相加相・乗平均の関係だと思います。この不等式はいろんな問題で利用できますから。
<かず子>確かに相加・相乗平均の応用範囲は広いけど、それは「代表的」な不等式ということであって、エライということではないと思うわ。
<まなぶ>そうだよな。だいたいエライ奴ってのはあまり働かないものだものな。
<先 生>(まなぶを無視して)かず子は、どうして相加・相乗平均ではないと思うんだい。
<かず子>だって相加相乗平均の関係は、負でない2数に対しての不等式だから、他の不等式に比べて値が制限されているもの。
<よしお>そんなことはないと思うな。平方数は必ず0以上の値なんだから、2つの平方数に対して使えばいいんじゃないのかな。例えば、
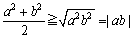 故に
故に 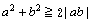
この式は、すべての実数a,bで成立するだろう。
<かず子>そういわれれば確かにそうね。あっ、でもその式、x2,y2,z2の適当な2つの文字で使うと、
x2+y2≧2|xy|,y2+z2≧2|yz|,z2+x2≧2|zx|
となるから、各式を辺々加えると、
x2+y2+z2≧|xy|+|yz|+|zx|
なんか③ぽいのがでてくるわ。
<先 生>けがの功名ってところだね。ところで|x|とxの大小関係はどうなっていたろう。
<よしお>|x|≧xで、等号成立は、x≧0です。
<先 生>そうすると、
x2+y2+z2≧|xy|+|yz|+|zx|≧xy+yz+zx
等号成立は、x2=y2,y2=z2,z2=x2 かつ xy≧0,yz≧0,zx≧0 より、x=y=zのときだ。
<かず子>思った通り、①の方が③よりエライんですね。
<まなぶ>確かに、③は名もない不等式だから、それと比べたら、やっぱり天下の相加・相乗平均の方がエライんだろうな。そうするとあとは、①と②の勝負ですね。僕はやっぱり②を押すな。
<先 生>それじゃ、まなぶの論理性のまったくない感を尊重して、②から①を証明してみようか。どうすればいいだろう。
<かず子>②の左辺は2多項式の積ですから、①のようにするには、x,yをなんとかしなくちゃいけないですよね。
<まなぶ>x=y=1にしたらどうだろうか。そうすると、
2(a2+b2)≧(a+b)2
右辺を展開して整理すると、
a2+b2≧2ab
あとは、A=x2,B=b2と置き換えてやればいいんだ。
どうだい。先生、僕ぐらいの山勘になると、感性だけで数学の論理性を従わせることができるんだ。
<先 生>x=y=1と置いたのはけっして山勘ではないよ。コーシーの等号成立を相加・相乗平均のそれに変えるには、a:b=x:yにおいて、x=y=1とおくと、a=bがでてくるだろう。至極当然なことなんだよ。ちなみに、
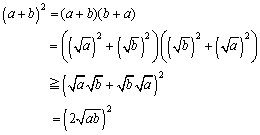
ともできる。
<まなぶ>先生は、僕のこと、よほど認めたくないんですね。あてつけにに別証明まで紹介なんかしたりして。でも、これで②が一番エライという僕の予想は正しかったことになりますね。
<先 生>本当にそうだろうか。
<まなぶ>先生、そこまでいうと負け惜しみも嫌味だよ。
<よしお>いや、まなぶ、僕も実は気になっていることがあるんだ。さっき、まなぶが②から①を示すのに、x,yを置き換えただろう。同じような置き換えを③でも考えてみるんだ。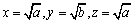 とおくよね。そうすると③は、
とおくよね。そうすると③は、
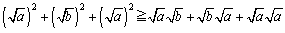
整理して 
これから、①が示されてしまうよね。
<まなぶ>あれっ、本当だ。そうすると、①と③のどっちがえらいということになるんだろう?。でも、どちらにせよ、②が一番エライことは変わらないからいいけどね。
<かず子>まなぶ。よしおがいおうとしていることは、③から①がだせたということは、①から②もだせる可能性があるということじゃないかしら。
<よしお>そうなんだ。先ほどの先生の言葉を聞くと、それも可能のように思えるんだけど。
<先 生>まっ、結論は置いといて、片方からもう片方をだしただけでは、不十分ということは分かるよね。では逆が可能かどうかの確認をしてみようか。そのためには、相加・相乗平均の関係を使えるようにコーシーの左辺を2数の和にする必要がある。
糸口をみつけるために展開してみると、
(a2+b2)(x2+y2)=a2x2+a2y2+b2x2+b2y2
この式が相加・相乗平均の関係を使って、(ax+by)2に変形できればいい。
<まなぶ>a2y2+b2x2が、2axbyになれば、いいんですよね。あっ、そうか、先生、できます。
a2y2≧0,b2x2≧0だから、この2数に相加・相乗平均の関係を使うと、
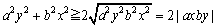
これから、
(a2+b2)(x2+y2)≧a2x2+2|axby|+b2y2
≧a2x2+2axby+b2y2
=(ax+by)2
どうですか?
<先 生>うむ。正解だ。これで、①から②を導きだすこともできたということになる。それではだ。結局一番エライ不等式ってどれなんだろう。
<生徒達>………。
<よしお>先生の質問の仕方、おかしいと思いますが。いままでのことから、①と②、①と③はどちらを使っても他方が導き出せるってことでしたから、①の相加・相乗平均を仲立ちとして、②と③もお互いを導き出すことができるということになりますよね。そうしたら結局①,②,③どれをとっても優劣なんか、つけられないということになりませんか。
<先 生>その通りだね。だから、結局①,②,③の不等式どれもが一番エライということだ。
<まなぶ>そういういいかたをするとどの不等式もえらくないともいえますよね。うーん。先生らしくないと思うな。今回はオチはないんですか。
<先 生>あのな。先生は落語家ではないよ。不等式はオチをつけるほど易しい問題ではないよ。これらの不等式がお互いどう絡んでいるかというのは、深く深~く研究しなければ見えてこない。オチて、ずーと底に沈んでいるものを敢えて考えるなら、①,②,③どの不等式の証明をみても平方完成することに帰着するから、不等式a2≧0が横たわっているのかもしれないね。
<まなぶ>先生、それってオチをいったつもりなんですか?。
| |α+β|≦|α|+|β| ……① |
は、α=a+bi,β=x+yiとおくと、
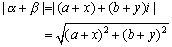
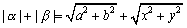
これから
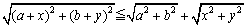
なる絶対不等式が得られます。
この両辺を平方して整理すると、
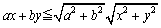
となり、コーシーの不等式に一致してきます。
なお、三角不等式は、この形で考えれば、ミンコフスキーの不等式
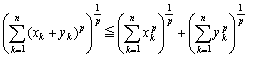 (xk>0,yk>0,p>1) ……② (xk>0,yk>0,p>1) ……② |
に拡張でき、後述するようにコーシーの不等式と深いつながりをもってきます。したがって、高校2年生レベルを想定すれば、三角不等式をエライ不等式候補にいれてもよかったかもしれません。
さて、ところで、相加・相乗平均や、コーシーの不等式の根源を調べるのではなく、逆に拡張していくと、どんな不等式が得られるのでしょうか。積分の形への拡張については、「コーシーの不等式のちょっとした小手技」を参考いただければと思います。ここでは、単純に変数の個数の拡張で考えてみましょう。
まず、コーシーの不等式ですが、n変数では、
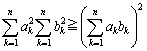 (等号成立は、ak=tbkのとき) ……③ (等号成立は、ak=tbkのとき) ……③ |
となり、この不等式は、ヘルダーの不等式、
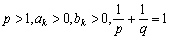 のとき、 のとき、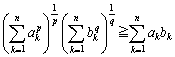 ……④ ……④ |
に拡張され、さらにイエンゼンの不等式としてまとめらます。
次に、相加・相乗平均ですが、調和平均を組合わせた関係は、幾何学的証明の美しさとしてよく知られるところです。
ak>0のとき、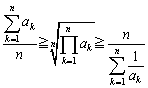 (等号成立はa1=a2=・・・=anのとき) ……⑤ (等号成立はa1=a2=・・・=anのとき) ……⑤ |
なお、相加平均≧調和平均 は、コーシーの不等式から簡単に証明することができます。
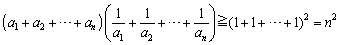
これから、
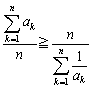
を得ます。さらに、相加・相乗平均の関係についてはコーシーの不等式から導くことも可能です(コーシーの不等式の小手技参照)。
ここで、ちょっと別角度からこの3つの平均を眺めてみましょう。
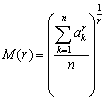
とおくとき、これをak(k=1,2,3,・・・,n)のr次平均といいますが、相加平均、調和平均は、それぞれ、M(1),M(-1)と表させます。
では、相乗平均はどうかというと、M(0)となることが次のようにして示されます。
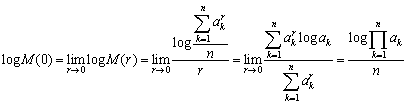
故に、
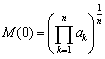
を得ます。
以上より、
M(1)≧M(0)≧M(-1)
なる面白い関係がみつかります。
話をもとに戻しましょう。
本文は、有名絶対不等式で一番エライ不等式は何かを調べる問題でした。不等式を生み出す根源の不等式は何かということです。結論は、「みんなえらかった」という、まなぶが述べているように不満の残る結果でした。結局、何かこれ以外に根源の不等式があるのではないかという疑問を残したまま本文は終わっています。オチていった底にa2≧0を提案していますが、ここまでいってしまうと、不等式の基本性質に帰着しまって余りにつまらない結論でしょう。では、相加・相乗平均とコーシーの不等式をともに生み出すような不等式はないのでしょうか。実はしっかりと存在し、その名前をベルヌーイの不等式といいます。
|
x>0で、0<r<1のとき、xr-1≦r(x-1) (等号成立は、x=1のときである) ……⑥ |
この不等式の証明は、微分に拠ります。
証明)f(x)=xr-rx+r-1とおく。
f'(x)=rxr-1-r=r(xr-1-1)
f"(x)=r(r-1)xr-2
ここで、f'(1)=0,f"(1)<0あるから、
f(x)は、x=1で極大値(最大値)f(1)=0をとる。
f(1)=0であるから、以上より f(x)≦0
このベルヌーイの不等式を使って、次の不等式が証明できます。
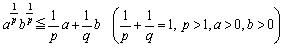 ……⑦ ……⑦ |
証明)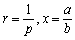 とおきます。
とおきます。
0<r<1より、1<pとなり、ベルヌーイの不等式に代入すると、
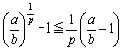
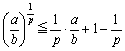
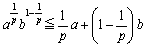
ここで、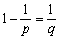 とおくと、⑦の不等式を得ます。
とおくと、⑦の不等式を得ます。
では、この⑦の不等式を利用して、相加・相乗・調和平均の関係およびコーシーの不等式を導き出してみましょう。
《相加・相乗・調和平均》
証明) ⑦において、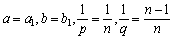 とおくと、
とおくと、
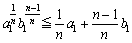
さらに、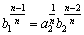 とおくと、
とおくと、
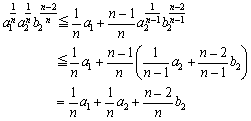
次に、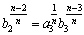 とおくと、
とおくと、
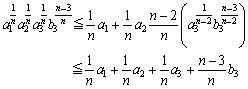
以下、順次、この置き換えを続けていくと、
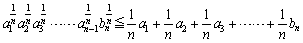
最後に、bn=anとおくと、
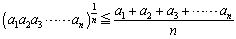
が得られます。
また、相乗平均≧調和平均の関係については、逆数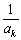 について、相加・相乗平均の関係を使うと、
について、相加・相乗平均の関係を使うと、
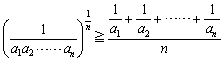
これより、証明されます。
《ヘルダーの不等式とコーシーの不等式》
証明) ⑦の不等式において、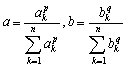 とおき、代入します。
とおき、代入します。
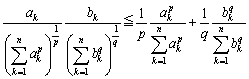
ここで、k=1,2,・・・,nとして、各不等式を辺々加えると、
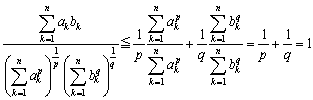
以上より、
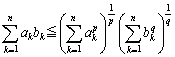
さらに、ここで、p=q=2とおくと、コーシーの不等式が得られます。
以上より、相加・相乗平均、ヘルダー、コーシーの不等式の根源的な不等式はベルヌーイの不等式であることが分かりました。
さらに、ヘルダーの不等式を利用すると、
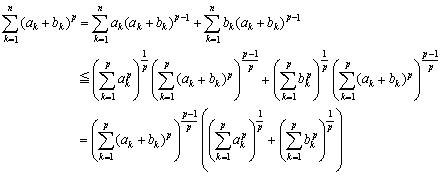
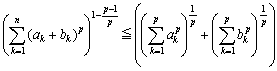
これから、②のミンコフスキーの不等式も得られます。
本文においても、ここまで触れると、まなぶの不満はすっきりと解消されることになるのでしょうか?。
ところがです。相加・相乗平均の関係は帰納的に証明できることは既知の通りです。
そうやって得られる相加・相乗平均の関係を、
a1=a2=a3=・・・=am=x, am+1=am+2=am+3=・・・=an=1
として使うと、
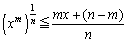
さらに、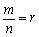 とおくと、
とおくと、
xr≦rx+(1-r)
よって、ベルヌーイの不等式が得られてしまいました。
ということは、ベルヌーイの不等式よりエライ不等式は、相加・相乗平均の関係となります。
また、振り出しに戻ったわけです。この議論、結局いつまでたっても落ちていく底が見つからないのです。
まなぶの気分が晴れることはないのかもしれません。