無限等比級数の収束を見る

札幌藻岩高等学校　中村文則

　初項

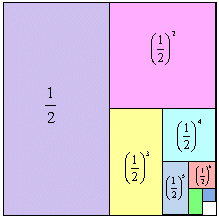
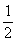、公比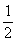

の無限等比級数は正方形の面積を利用することで図のように１に収束することを見ることができます。同様に、収束する無限等比数列の和を三角形を分割した面積の和とみて視覚的に表現することを考えて見ましょう。

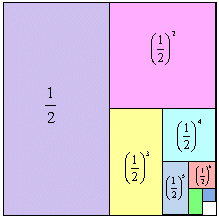
(1) 公比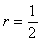の無限等比級数
　　　
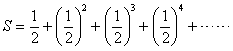
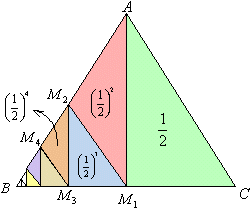
△ABCにおいて、BCの中点をM₁とすると、
　　　
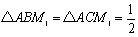
△ABM₁において、ABの中点をM₂とすると、
　　　
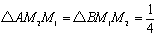
以下同様に、右図のように中点をとっていくと、
　　　
　　　

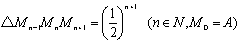
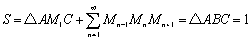
(2) 公比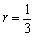の無限等比級数
　　　
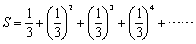
三角形ABCの重心をG₁とすると、
　　　
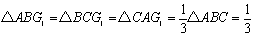
次に△G₁BCの重心をG₂とすると、
　　　
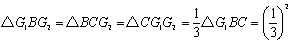
以下同様に、中線AM上に重心をとっていくと、
　　　
　　　

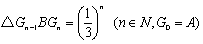
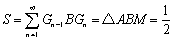
(3) 公比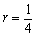の無限等比級数
　　　
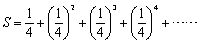
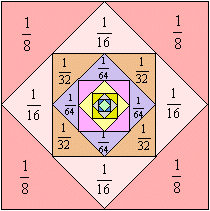
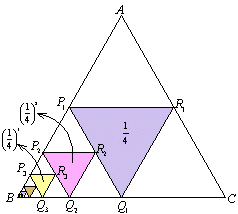
三角形ABCの各辺AB，BC，CAの中点をそれぞれP₁，Q₁，R₁とします。
　　　
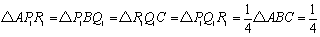
△P₁BQ₁の各辺P₁B，BQ₁，Q₁P₁の中点をそれぞれP₂，Q₂，R₂とすると、
　　　
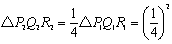
となります。
以下同様にP_n，Q_n，R_nをとっていくと、
　　　
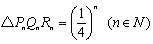
よって、
　　　
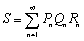
ここで、
　　　T_n=四角形P_n-1P_nQ_nQ_n-1の面積　（n∈N，A=P₀，C=Q₀）
とおくと、
　　　T_n：△P_nQ_nR_n=3：1
　　　∴　

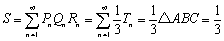
(4) 公比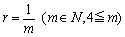の無限等比級数
　　　
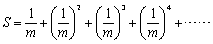
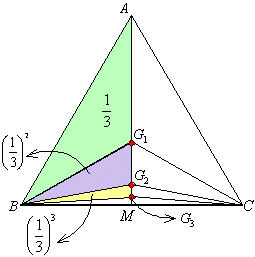
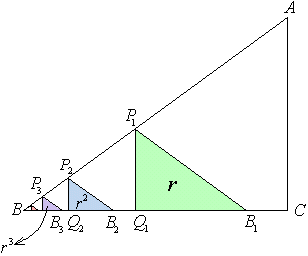
三角形ABCの辺AB，CB上にそれぞれ、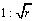となる点P₁，Q₁をとり、さらに辺CB上に、Q₁B=Q₁B₁なる点B₁をとると、
　　　△P₁Q₁B₁=△P₁BQ₁=r△ABC=r
　次に△P₁BQ₁の辺P₁B，Q₁B上にそれぞれ、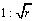となる点P₂，Q₂をとり、辺BQ₁上に、Q₂B=Q₂B₂なる点B₂をとると、
　　△P₂Q₂B₂=△P₂BQ₂=ｒ△P₁BQ₁=r²
　以下、同様に△P_nQ_nB_nを作ると、
　　　△P_nQ_nB_n=rⁿ
よって、
　　　
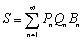
となります。
　ここで、
　　　△P_n-1BQ_n-1：△P_nQ_nB_n=1：ｒ　（n∈N，A=P₀，C=Q₀）
ですから、
　　　T_n=四角形P_n-1P_nQ_nQ_n-1の面積
とおくと、
　　　T_n：△P_nQ_nB_n=1-r：r
　よって、
　　　
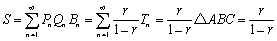
(1),(2),(3),(4)より、公比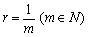について、無限等比数列の和を見ることができました。

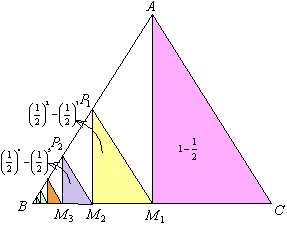(5) 公比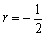の無限等比級数
　　　
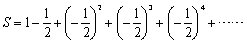
　三角形ABCにおいて、辺BCの中点をM₁とすると、
　　　
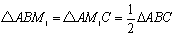
　よって
　　　
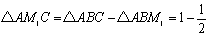
次に辺ABの中点をP₁とすると、
　　　
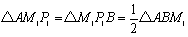
さらに辺BM₁の中点をM₂とすると、
　　　
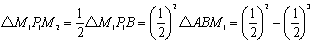
以下同様の操作を続けていくと、
　　　
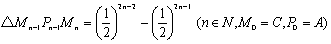
ここで、
　　　T_n=四角形P_n-1P_nM_nM_n-1の面積
とおくと、
　　　T_n：△M_n-1P_n-1M_n=3：2
ですから、
　　　

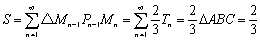
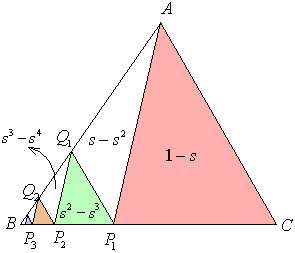(6) 公比r（-1＜r＜0）の無限等比級数

　　　S=1+r+r²+r³+・・・
　　　R=-s（0＜s＜1）
とすると、
　　　S=1-s+s²-s³+s⁴+・・・
三角形ABCにおいて、辺BCをs：1-sの比に内分する点をP₁とすると、
　　　△P₁AB=s，△P₁CA=1-s
辺BAをs：1-sの比に内分する点をQ₁とすると、
　　　△P₁Q₁B=s△P₁AB=s²
辺BP₁をs：1-sの比に内分する点をP₂とすると、
　　　△P₁Q₁P₂=(1-s)P₁Q₁B=(1-s)s²=s²-s³
以下同様の操作を続けていくと、
　　　△P_n-1Q_n-1P_n=s^2n-2-s^2n-1（P₀=C，Q₀=A，n∈N）
　またT_n=四角形Q_n-1Q_nP_nP_n-1の面積とおくと、
　　　T_n：△P_n-1Q_n-1P_n=1+s：1
　　　
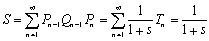
　　　したがって
　　　

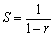
(7) 公比r（-1＜r＜1）の無限等比級数

(1)～(6)までで、公比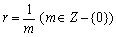の場合についてその収束をみることができました。
さらに、(４)の無限等比級数の証明は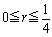である実数ｒについても成立するのは明らかですから(6)とあわせて、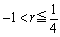および、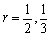で無限等比級数はその収束を三角形の面積として見ることができます。
では、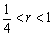なる実数ｒを公比とする場合はどうかというと、無限等比数列の和は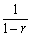で与えられ、
　　　
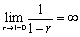
となりますから、面積１の三角形を分割して表現することは難しくなります。
　そこで、座標平面上の直線を利用することで、三角形の面積を切り出すことを考えてみましょう。
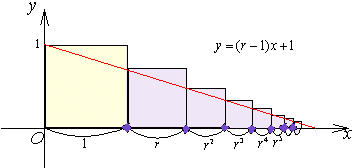
　等比数列の公比をr（0＜r＜1）とし、直線
　　　y=(r-1)x+1
を考えます。この直線とx軸との交点は、
　　　
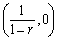
ですから、直線の傾きr-1から無限等比級数の収束、発散が分かります。
ここで、ｘに順次、
　　　1，r+1，r²+r+1，r³+r²+r+1，・・・
を代入すると、
　　r，r²，r³，r⁴，・・・
これから右図のように正方形を作っていくと、等比数列の無限個の和を見ることができます。
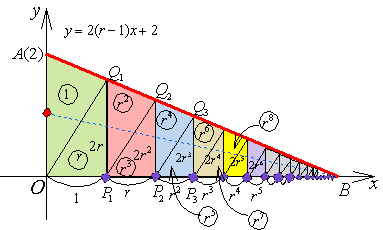　次に、直線y=(r-1)x+1をｙ軸方向に２倍に拡大した直線
　　　y=2(r-1)x+2
を考えてみます。
このとき、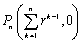に対応した直線上の点Q_nは、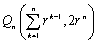となります。
したがって、
　　　S_n=△Q_n-1P_n-1Q_nの面積，T_n=P_n-1Q_nP_nの面積　（P₀=0，Q₀=A）
とすると
　　　
　　　
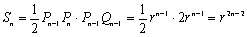
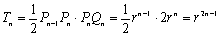
　これから
　　　
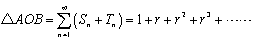
となります。また、
　　　
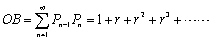
極限は線分の長さと、三角形の面積の両方でみることができます。
　以上より、公比0＜r＜1の場合もその収束を三角形の面積として表現できますから、-1＜r＜1のすべての収束が目で見ることができるようになりました。