
栤戣俀
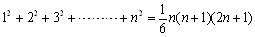 偱偁傞偙偲傪巊偭偰偔偩偝偄丅
偱偁傞偙偲傪巊偭偰偔偩偝偄丅
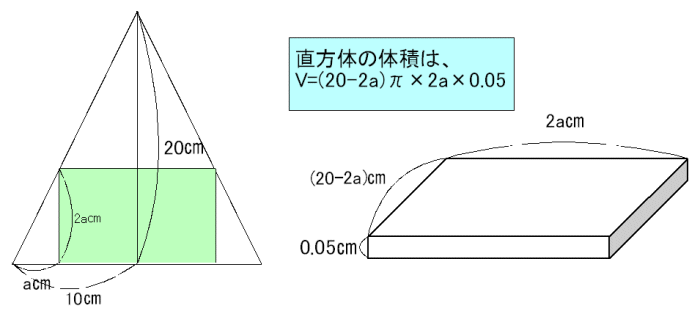
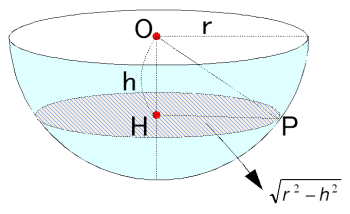
丂侾夞傝傎偖偟偨墌廃(挿曽宍偺墶偺挿偝)偼奜懁偐傜弴偵
丂丂丂(20-0.1)兾,(20-0.2)兾,(20-0.3)兾,乧乧,(20-19.8)兾,(20-19.9)兾
偲側傝傑偡丅
丂摨條偵丄傎偖偟偨挿曽宍偺廲偺挿偝偼奜懁偐傜弴偵
丂丂丂0.1,0.2,0.3,乧乧乧,19.9
偲側傝傑偡丅
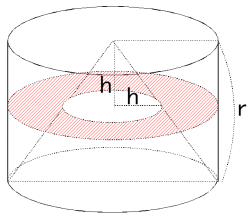
丂偟偨偑偭偰偦傟偧傟偺挿曽宍偺柺愊偵巻偺岤偝0.05噋傪妡偗偨捈曽懱偺懱愊偺榓V偼丄
丂丂丂V= (20-0.1)兾亊0.1亊0.05
丂丂丂丂+(20-0.2)兾亊0.2亊0.05
丂丂丂丂+乧乧乧乧
丂丂丂丂+(20-19.8)兾亊19.8亊0.05
丂丂丂丂+(20-19.9)兾亊19.9亊0.05
丂丂丂={2亊(1+2+3+乧乧+199)-(0.1)2(12+22+32+乧乧+1982+1992)}亊0.05兾
丂偙偙偱丄丂1+2+3+乧乧+199= 1/2亊199亊200=19900
丂傑偨丄12+22+32+乧乧+1982+1992=1/6亊199亊200亊399=199亊100亊133
偲側傝傑偡丅
丂埲忋傛傝懱愊V偼
丂丂丂V={2亊19900-199亊133}亊0.05兾=199亊67亊0.05兾=666.7兾(cm3)
丂偙傟偐傜懱愊偼丄栺2093(cm3)偲側傝傑偡丅
栤戣俁
楙廗栤戣
栤戣侾
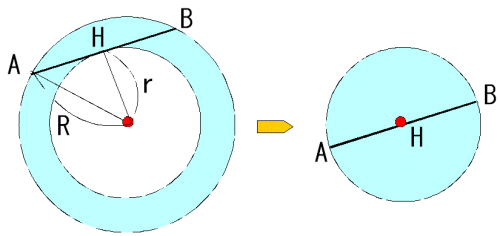
栤戣俀
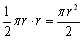
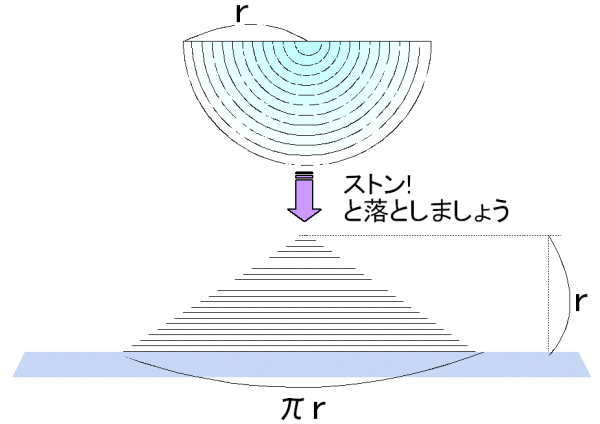
栤戣俁
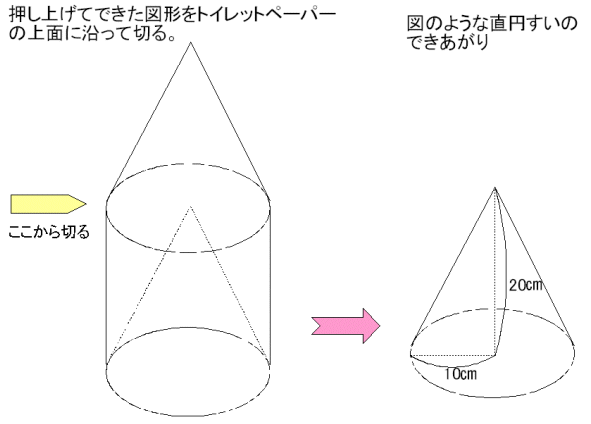
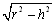 偱偁傞墌偺柺愊偵堦抳偟傑偡丅偙傟傪愊傒廳偹傞偲恾傛傝丄
偱偁傞墌偺柺愊偵堦抳偟傑偡丅偙傟傪愊傒廳偹傞偲恾傛傝丄
栤戣係
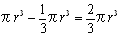
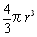
丂杮峞偼丆悢妛婎慴偺曗彆揑嫵嵽偺堦椺偲偟偰採埬偡傞傕偺偱偁傞丏
丂悢妛婎慴偱偼丆偦偺巜摫偼乽恖娫乿傗乽幮夛惗妶乿傪僉乕儚乕僪偲偟偰丆恎嬤側帠徾偺悢棟揑峫嶡傪偡傞偙偲傪梫媮偟偰偄傞丏偨偩丆棟榑揑側峫嶡偼怺擖傝偟側偄偲偄偆敍傝傕偁傞偨傔丆帺慠偲捈姶揑側傾僾儘乕僠偱偺揥奐偲側傞丏傑偨丆峫嶡偺堦庤抜偱偁傞乽寁嶼乿偵偮偄偰傕嬌椡攔彍偟丆峫嶡偟側偗傟偽側傜側偄丏乽偱偒傞乿偙偲傛傝傕乽傢偐傞乿偙偲偑廳帇偝傟偰偄傞偺偱偁傞丏
丂摉慠丆恎嬤側帠徾偼恎嬤側慺嵽偐傜峫嶡偺擖岥傪峫偊傞偲慻傒偟堈偄偙偲偵側傞丏偩偐傜丆僩僀儗僢僩儁乕僷乕偼岲椺偲偄偊傞丏偦偺慺嵽偺廮傜偐偝偼丆僶乕儉僋乕僿儞忬偵姫偒偮偄偨恾宍傪偄偐傛偆偵傕壛岺偑偱偒傞丏枅擔巊梡偟偰偄傞乽僩僀儗僢僩儁乕僷乕乿偺懚嵼姶偲偦偺姶怗偺乽廮傜偐偝乿偼丆拪徾揑側僀儊乕僕傪傕廮傜偐偔偟丆憐憸忋偱丆梕堈偵壛岺偺曄壔傪捛偭偰偄偗傞偺偱偁傞丏
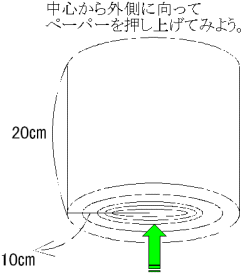
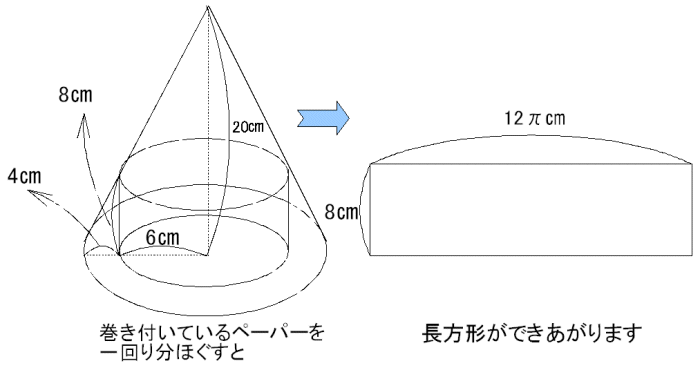
丂杮峞偱偼丆僩僀儗僢僩儁乕僷乕傪巊偭偰丆僇僶儕僄儕偺尨棟偵傛傞愊暘奣擮偺巜摫傪帋傒偰偄傞丏廬棃傛傝丆墌拰偺懱愊傗儁乕僷乕傪堷偒怢偽偟偨偲偒偺巻偺挿偝偺媮傔曽偵偮偄偰偼椙偔抦傜傟偰偄傞偙偲偱偁傞偑丆偙偙偱偼丆僩僀儗僢僩儁乕僷乕傪拞怱偐傜墴偟崬傒愗傝庢偭偰偱偒傞捈墌偡偄偺懱愊偲丆巆偭偨晹暘偺僩僀儗僢僩儁乕僷乕偐傜媴偺懱愊傪媮傔偰偄傞丏
丂偨偩丆傛偔峫偊傟偽丆杮暥偱愢柧偟偰偄傞傛偆側宍偱墌偡偄偺廃傝偵儁乕僷乕偑姫偒庢傜傟傞傢偗偱偼側偄偙偲偼丆婥偑晅偔偲巚偆丏廮傜偐側拪徾揑僀儊乕僕傪媡庤偵庢偭偨婾傝偱偁傞丏幚嵺偵偼儁乕僷乕偼墌偡偄偵梿慁忬偵姫偒晅偄偰偄偔偼偢偱偁傞丏杮暥偺傛偆側姫偒偮偒曽偺捈墌偡偄傪嶌傞偵偼丆墌拰傪嶍偓愗偭偰丆偔傝敳偐側偗傟偽側傜側偄丏
丂傑偨丆恾偱峫偊偰偄傞僩僀儗僢僩儁乕僷乕偺僒僀僘偼丆敿宎10們倣丆崅偝20們倣偱偁傞偐傜丆偢偄傇傫偱偐偄丏幚嵺偺戝偒偝傪寁應偡傞偲丆(変偑壠偱巊梡偟偰偄傞傕偺偼)敿宎6們倣丆崅偝12們倣埵偱偁傞偐傜丆偄偔傜側傫偱傕偙偺戝偒偝偼側偄偩傠偆丆偲偄偆偙偲偵側傞丏偝傜偵丆杮暥偱偼悢楍偺榓傪寁嶼偝偣偰偄傞偑丆偙傟偼慜弎偟偨悢妛婎慴偵偍偗傞乽寁嶼偺攔彍乿偺栤戣偵掞怗偡傞丏帺慠悢偺榓偖傜偄偼丆僈僂僗彮擭偺傾僀僨傾偱娙扨偵愢柧偱偒傞偑丆暯曽悢偺榓偼偦偆偼偄偐側偄丏偩偐傜嫵壢彂偵偍偄偰傕偙偺寁嶼偺埖偄偼偢偄傇傫偰偙偢偭偰偍傝丆巜摫梫椞偵増偆偨傔偵丆梐嬥偺暋棙朄偺傛偆偵巭傓傪偊偢寁嶼偑昁梫側応崌偼揹戩傪棙梡偝偣偰偄傞偺偱偁傞丏
丂偩偑丆幚嵺偵偼悢妛揑巚峫偼抦宐(傾僀僨傾)偲抦幆(寁嶼)偺椉椫偱惉傝棫偮傢偗偩偐傜寁嶼傪100亾攔彍偡傞偙偲側偳偁傝偊側偄丏抦宐傪巊偭偰乽柺搢側寁嶼傪岺晇偟偰娙扨偵偡傞乿偙偲傕悢妛偺戝帠側巚峫偱偁傞偟丆抦幆偲抦宐偼撈棫偟偨幵椫偱偼側偔悢妛揑巚峫偲偄偆僄儞僕儞偵捈寢偟偨嬱摦椫偲峫偊傞傋偒側偺偱偁傞丏
丂偟偐偟丆杮峞傪扨撈偺暘栰偲懆偊傞偺偱偼側偔丆杮棃偺悢妛偑偦偆偱偁傞傛偆偵懠暘栰偲偺桳婡揑寢崌偺忋偵惉傝棫偮偲峫偊傞側傜偽丆僩僀儗僢僩儁乕僷乕偺戝偒偝偺栤戣偼丆棫懱偺憡帡斾傪埖偆暘栰偲棈傔傟偽傛偄丏暯曽悢偺榓偵偮偄偰偼丆僺儔儈僢僪忬偵攝楍偟偨悢偺攝楍偐傜帇妎揑偵尒弌偡偙偲偼傛偔抦傜傟偰偄傞偐傜丆尰抧挷払揑偵帠慜巜摫偡傞偙偲偼壜擻偱偁傞丏偦偆偄偭偨壽戣夝寛偺嵼傝曽偺乽廮傜偐偝乿傕悢妛婎慴偺巜摫偵偼昁梫晄壜寚偲側偭偰偔傞丏
丂婎杮揑偵悢妛婎慴偼侾偐傜偺弌敪偱偁傞丏暘栰偺奣擮揑側崪巕偼嫵壢彂偵埖傢傟傞偑丆偦傟傪掕拝偝偣傞偨傔偺擏晅偗偼偢偄傇傫尰応偺忬嫷偵傛偭偰堘偭偰偔傞偩傠偆丏儈僯儅儉偼侾偩偑丆儅僢僋僗偼尷傝側偔晄掕側抣偱偁傝丆尰応愝掕偺摓払栚昗偵傛偭偰寛掕偝傟傞丏
丂偦偟偰丆偄傛偄傛暯惉侾俆擭係寧丆悢妛婎慴偼戝偄側傞壽戣傪傕偭偰丆尰応偵嶲擖偡傞丏