
札幌藻岩高校 中村 文則



札幌藻岩高校 中村 文則


 【材 料】 本時で使用する素材
【材 料】 本時で使用する素材
【下ごしらえ】
 【調 理】
【調 理】
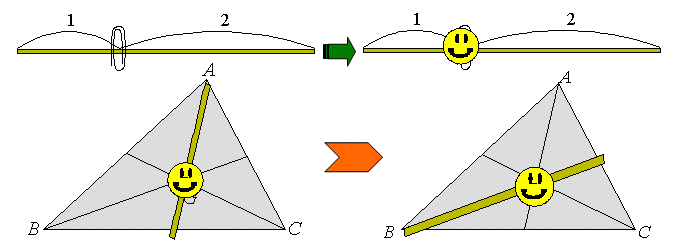
《基本編1》 〜重心をメイクる
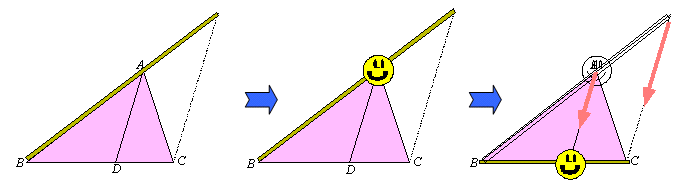
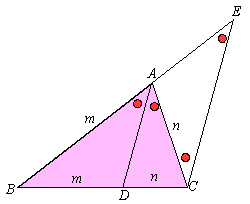 証明)
証明)AE=ECより三角形ACEは二等辺三角形。 ∴ ∠ACE=∠AEC また、∠AEC+∠ACE=∠BAC ここで、線分ADは角Aの二等分線であるから、 ∠BAD=∠CAD=∠AEC=∠ACE よって、∠DAC=∠ACEより、DA//CE(錯角が等しい) 以上より、 AB:AC=BA:AE=BD:DC |

|
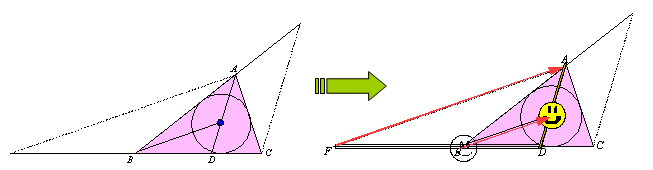
「ジェラシー大作戦」 ある高校にアイドルちゃんと呼ばれる女の子がいる。彼女は容姿もプロポーションも抜群で、しかも努力家であると言う。彼女は陸上部に所属し、放課後はいつも陸上グランドで走る練習をしている。一方、あこがれ君は同じ学校でのサッカー部のゴールキーパーである。アイドルちゃんに熱烈に恋焦がれており、放課後はゴールキーパーの位置から走っている彼女に、いつもラブサインを送りつづけている。 このことを知ったジェラシー君の心境はおだやかでない。彼は、あこがれ君の意図をなんとか妨害しなければと固く決意し、視察を続けた結果、次のことに気がついた。 あこがれと、君アイドルちゃんを結ぶ線分を2:1に内分する点に彼が立つと、彼に遮られてあこがれ君からはアイドルちゃんが見えなくなってしまうのである。 ジェラシー君の妨害作戦が成功するためには、彼はどのような走り方(動き)をしたらよいだろうか。
………大山斉先生著 「教具の工夫〜いくつかの実例〜」から原文引用
|

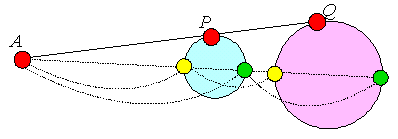
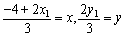 より、
より、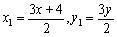
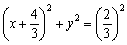

| 定点と猫を結ぶ線分を1:1の比に内分する点の軌跡 |

| 定点と蝶を結ぶ線分を3:2の比に外分する点の軌跡 |
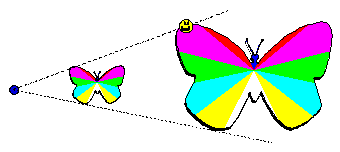
まとめ
簡単な興具の代表選手は、輪ゴムであることは、異論のないことだと思います。
伸び縮みが可能な輪ゴムは、トポロジカルな話題を提供します。初期の頃の数実研の研究発表においても、安房先生(当時札幌東校)がゴムひもで分点の軌跡を視覚提示したことは、まだまだ記憶に新しいことです。そして、そのアイデアをベースとして、同僚であった大山先生(現双葉高校)により「ジェラシー大作戦」が生み出されました。
無味乾燥な式の羅列になりがちであった分点の軌跡の説明が見事にドラマとして蘇ったのです。ただ、脚本は珠玉であっても、演出がつまらなければ、視聴率はがた落ちするものです。ここは演出家たる教師の力量が、問われる場面であるといえます。この場合、ゴムひもの利用は極めて有効な理解手段ではあるのですが、「アイドルちゃん」に教師が手を添えて動かすと、視聴者である生徒は、その方向に意識を集中してしまいます。アイドルちゃんがグルッと円を描いても、可哀想かな、ジェラシー君の動きは粗雑に扱われ、いつの間にか「なにも残らぬ軌跡」を描き終わっているのです。そのことに演出家が気が付かなければこの時点でせっかくの脚本は死んだといえるでしょう。主役はアイドルちゃんでなくジェラシー君であり、ジェラシー君をどう引き立てるかが演出家の腕の見せ処なのです。
 さて、その一方法として、本文では、小興具「クリップとマグネット」を使っています。動点にクリップを挟み、そのクリップに厚紙で切り抜いた派手キャラなんかを挟んで動かすと、視聴者の視線はそちらに移動するものです。アイドルちゃんとジェラシー君の間を行き来する視線を操りながら、軌跡を埋めていきましょう。
さて、その一方法として、本文では、小興具「クリップとマグネット」を使っています。動点にクリップを挟み、そのクリップに厚紙で切り抜いた派手キャラなんかを挟んで動かすと、視聴者の視線はそちらに移動するものです。アイドルちゃんとジェラシー君の間を行き来する視線を操りながら、軌跡を埋めていきましょう。
ところで、マグネットも最近は随分凝ったものが売られてます。百円ショップを覗くと、あることあること(ちなみに、私の興具の大半は、ここで調達しています。蛇足ながら、生活必需品も)。貧乏教師にとっては大変有難い店ができたものです。本文中にある、「スマイルマーク」のマグネットは、4個もついて百円。この値段、感動ものです。興具を捜し求めて店内を一回りするいろんなアイデアが生まれてくるものです。
話が脱線してしまいました。本文の前半の部分についても、触れておきます。
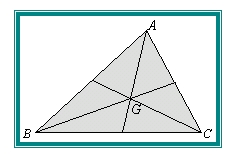
重心は「三中線の交点」ですが、「どうして中線が一点で交わるか」ということは、理論で分かっていても、体感は難しいものです。中線の1本を引き、2:1の比に内分する点にスマイルマークを貼り、他の中線上に移すと、最初に引いた中線上にスマイルマークが重なることが簡単に確認できます。垂心や外心についても同様に理解できるでしょう。
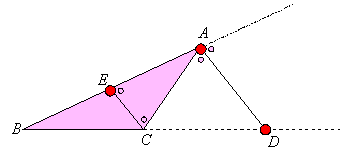
次に、角の二等分線分についてですが、角の比と線分の比を混同している生徒が意外と多いことに驚かされます。「角の二等分線と対辺との交点は、対辺の中点」と思っている生徒が随分いるのです。角の二等分線のコンパスでの作図は理解していても、三角形の内角を二等分する段階で、中線の考えが混じってしまうのでしょうか。これは「目見当による図形の作図」の典型的誤りではないかと思います。生徒が三角形ABCにおいて、内角Aの二等分線を引く場合、頂点Aから、対辺BCに向かって目検討で直線を引こうとします。人間の不器用な手は、自然と易きに流れ、BCの中点近くの点で結んでしまうのです。
本来、三角形の内角の二等分線は、本文でも説明している、AB:AC=BD:DCの関係をしっかりと押さえ(もちろんこの関係は外角の二等分線でも成立します)、まず、辺BC上に、分点Dをとってから、むしろ点Dから点Aへつなぎ、線を結ぶべきではないかと思います。この角の二等分線の性質は、方べきの定理や三平方の定理のような立派な名前を冠することもない数多くの三角形の性質の一つに過ぎないのですが、とても重要な性質であり、本文では内心の作図も試みています。
ところで、軌跡問題は、私にとっては実はとても思い入れの深い問題でもあります。線分を一定の比に分ける点の軌跡は、マジックハンドの腕の部分で説明されることは周知のことです。パンタグラフともいいます。
もう40年ほど昔になるでしょうか。両親に連れられて出かけた神社の縁日。チロチロとゆらめく提灯の灯を追って、境内につながる階段をワクワク登っていきます。両脇には、いっぱいの夜店が建ち並んでいます。威勢のいいお兄さんの掛け声に誘われて、ふと目を移すと、パンタグラフの器具を片手にもってお兄さんが、それを台の上においてパンタグラフの端点でアトムの絵をなぞり始めます。興味津々、キラキラ輝いた子供達の目がパンタグラフに注がれます。すると、端点の緩やかな動きに合わせて、関節部の一つに差し込まれた鉛筆が、縮小されたミニアトムを流れるように描いていくのです。いわゆる手製のコピー機(拡大・縮小機)です。その不思議な動きに心奪われて、両親にねだり買って貰ったのですが、残念ながら、1年もしないうちに紛失してしまいました。
やがて数学の教員になってから、その器具のことが無性に気になり始めたのです。だから、軌跡の授業はいつも次の言葉で結ぶことにしてます。
「先生が小さかった頃、縁日の夜店に、拡大機・縮小機が売られていたんだ。昔せっかく買ってもらったのになくしてしまったものだから、夜店をみると、先生いつも探して歩くんだけど、どこにもないんだよね。誰か、見たことのある人いないだろうか。いたら教えてください。」
まだ、朗報はありません。