

忳傟側偄傕偺傪忳傜側偄堊偵乧乧
丂悢妛偺廗摼偺夁掱偵偼丄忳傟傞傕偺偲忳傟側偄傕偺偑偁傞偲峫偊傞丅
丂悢妛俙偱偼丄場悢暘夝(忔朄岞幃)偺埫婰偼忳傟側偄傕偺偲偄偊傞丅扨偵揥奐偡傟偽丄偙傟傜偺岞幃偺徹柧偼娙扨側偺偩偑丄偩偐傜偲偄偭偰丄棟孅偱妎偊傞傕偺偱偼側偄丅岞幃偼摢偺拞偵扏偒崬傑側偗傟偽側傜側偄偺偩丅偦偟偰丄偦偺埫婰傪慜採偵弶傔偰丄摍幃丄晄摍幃偺徹柧偺傛偆側丄乽峫偊傞乿応柺偺栤戣偵庢傝慻傔傞偺偱偁傞丅
丂偩偐傜丄戝嶨攃偵尵偊偽丄忳傟側偄傕偺偼乽抦幆乿偱偁傝丄忳偭偰偄偄傕偺偼乽抦宐乿偲偄偆偙偲偵側傞偺偩傠偆偟丄抦宐偑抦幆傪忋夞傞偙偲偼堦斒偵偼偁傝偊側偄偺偱偁傞丅
丂偲偙傠偱丄悢妛嘥偺擇師娭悢偺暯曽姰惉乮堦斒宍偐傜昗弨宍傊偺曄宍乯傕丄忳傟側偄傕偺偱偁傞丅幉偺曽掱幃傗捀揰偑暘偐偭偰偙偦偺曻暔慄偺僌儔僼偱偁傝丄暯曽姰惉偑偱偒側偗傟偽壗堦偮栤戣偼夝偗側偄丅偩偑丄幚偼偙偺忳傟側偄傕偺偼側偐側偐庤嫮偄丅帟醳偄傑偱偵丄巚偆傛偆側掕拝偵偼帄傜側偄偺偱偁傞丅偩偐傜枅擭丄嫵巘偺嬯擸偼丄屲寧昦偲偲傕偵偙偙偐傜巒傑傞丅
丂偦偺憺偒暯曽姰惉偲偺埆愴嬯摤偺巜摫傪丄巚峫(帋峴偱偼側偄)嶖岆揑偵傑偲傔偰傒傛偆丅
仜棟憐揑曄宍朄
堦斒偵丄昗弨宍傊偺曄宍朄偺僗僞僀儖偼師偺傛偆側棳傟偵側傞丅
丂俀師幃偺曄宍偼丄
俶倧倲倕乯
丂偙偆偄偆寁嶼傪偡傞惗搆偼丄俀師偺崁偺師偵掕悢崁偺挷惍傪偟偰偟傑偭偨偨傔偱偁傝丄摢偺拞偱偺儕僼儗僀儞偑偆傑偔偱偒側偺偱偁傞丅
仜僀儞僷僋僩揑曄宍朄
丂暯曽姰惉偱巊傢傟傞岞幃偼丄
丂偱偁傞偑丄偙傟偼丄姰慡暯曽幃偲傒傞傋偒偱偼側偄丅
偲傒偰丄擇忔嵎偺岞幃偲傒傞曽偑帺慠偱偁傠偆丅暯曽姰惉偼丄俀師丄侾師偺崁傑偱挷惍偱偒傟偽丄掕悢崁偼偍傑偗偵傇傜壓偑偭偰偄傞傒偨偄側傕傫偱偁傞丅偝傜偵丄倫亖俀倎 偲偍偗偽丄
偙偺嵍曈偐傜塃曈偺曄宍傪
丂丂丂丂丂丂丂敿暘堷偔俀忔
偲偄偆偙偲偽偱報徾偯偗偰傒傛偆丅
丂敿暘堷偔俀忔偲彞偊偮偯偗偰偄傟偽側傫偲偐側傞偺偩偑丄幚嵺偵惗搆偵傗傜偣偰傒傞偲丄妵屖偱妵偭偰妵屖傪偼偢偡偲偄偆嶌嬈偑偄傑偄偪忋庤偔偱偒側偄丅摿偵丄俀師偺崁偺學悢偑丄晧悢偱偁偭偨傝丄暘悢偱偁偭偨傜乮晧悢偺暘悢偩偭偨傜嵟埆乯偍庤忋偘偱偁傞丅壗偲偐俀師偺崁偺學悢傪堄幆偟側偄偱寁嶼偱偒側偄傕偺偐偲峫偊偨偺偑師偺曽朄丅
仜僗儕儉揑曄宍朄
椉曈傪俀師偺崁偺學悢偱妱傞偲丄
丂偙偺曄宍朄偼丄曄宍偺棳傟偐傜傒傟偽丄椉曈傪妱傞偲偄偆憖嶌偐傜丄寁嶼偺夁掱偑侾僗僥僢僾抶傟傞傕偺偱偁傞偑丄偦偺寁嶼撪梕偼嬌傔偰扨弮偱丄妋幚側傕偺偱偁傞丅
丂敿暘堷偔俀忔偺僀儊乕僕偑偁傟偽扤偱傕娫堘偄側偔偱偒傞丅俀師偺崁偑丄晧悢偱偁傠偆偑丄暘悢偱偁傠偆偑傑偭偨偔巟忈偼側偄丅妵屖偺庢傝奜偟偺傛偆偵摢傪捝傔傞偙偲偼側偄偺偱偁傞丅壗偲側偔慡懱傪俀師偺崁偺學悢偱妱傞偙偲偵丄掕悢崁偺寁嶼偑柺搢偵側傞傛偆側報徾傪庴偗傞偑幚嵺偼丄傓偟傠寁嶼偼妝側応崌偺曽偑懡偄乮偄傠偄傠偲傗偭偰傒偨寢壥偐傜偺寢榑乯丅
丂偨偩丄嵟屻偺抜奒偱丄俀師偺崁偺學悢傪尦偵栠偡偺傪朰傟傞惗搆偑偄傞偲偄偆婋尟惈偑崅偄偺偑擄揰偱偼偁傞偑丅
仜僶僀僷僗揑曄宍朄
丂扨弮偵暯曽姰惉傪偟偰偟傑偆庤傪堦偮徯夘丅
丂偙傟偼丄x偺峆摍幃偱偁傞偐傜丄塃曈偺倶偵揔摉側抣傪戙擖偡傟偽丄q偼媮傔傜傟傞丅
丂埲忋偺偙偲傛傝丄師偺傛偆側暯曽姰惉偑峫偊傜傟傞丅
丂偲傝偁偊偢丄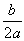 傪寁嶼偟偰丄姰慡暯曽幃傪嶌傞丅
傪寁嶼偟偰丄姰慡暯曽幃傪嶌傞丅
偲偡傞丅偁偲偼丄嘆丆嘇偺倶偵揔摉側悢抣傪戙擖偟丄偦偺嵎傪偲傟偽q偺抣偲側傞丅
椺偊偽丄嘇偺妵屖撪偺抣傪峫椂偟偰丄倶亖亅侾傪戙擖偡傞偲丄
偲側傞丅
Ex)
丂偙偺偲偒倶亖侽偺応崌偑捠忢偺暯曽姰惉偺夁掱偱摼傜傟傞寁嶼偱偁傞偑丄偦傟偵斾傋丄倶亖侾傪戙擖偟偨曽偑寁嶼偼悘暘妝側偙偲偵婥偑偮偔丅梫椞偝偊丄撣傒崬傔偰偟傑偊偽丄娙扨偵暯曽姰惉偑偱偒傞偺偱偁傞丅抦幆偲偟偰偺暯曽姰惉偑丄乽戙擖偡傞嵟揔側抣傪峫偊傞乿偲偄偆抦宐偺晹暘偵偪傚偭偲孹偄偨曄宍朄偲偄偊傞偩傠偆丅丂丂
丂丂
仜枛婜揑曄宍朄
丂埲忋偺偄偢傟偺曽朄傕嫅愨偟偰偟傑偆惗搆傕巆擮側偑傜偄傞丅偦偆偄偆応崌偼巭傓廔偊側偄丅
丂偙傟傪埫婰偟傠偲偄偆偙偲偵側傞丅偙偺埫婰偼偦偆擄偟偄傕偺偱偼側偄丅敾暿幃丄幉偺曽掱幃偲偄傠偄傠側梫慺傪娷傫偩傕偺偩偐傜丄彨棃揑偵傕埫婰偟偰偍偄偨曽偑栶偵偨偮丅偨偩丄幚嵺偵偙傟傪巊偭偰暯曽姰惉偺寁嶼偟偰傒傞偲丄堄奜偲掕悢崁偺寁嶼偑栵夘側応崌偑懡偄偺偱偁傞丅椺偊偽丄倎偺抣傪暘悢抣偲峫偊偰傒傟偽暘偐傞偩傠偆丅寁嶼椡偑側偔丄棟憐揑曄宍偑偱偒側偄惗搆偵寢嬊偼寁嶼椡傪梫媮偟偰偟傑偆偙偲偵側傞丅
偁 偲 偑 偒
乽墌偭偰丄墌斦偱偟傚乿丂彫丒拞妛峑偺愭惗偲偍榖傪偡傞婡夛偑偁偭偨偲偒偵墌偺掕媊偑榖戣偲側偭偨丅
乽偊偭丠丄拞恎偑偁傞傫偱偡偐乿
乽擄偟偄栤戣偱偡偹偉乿
丂墌斦偲墳偊偨偺偼彫妛峑偺愭惗丅彫妛峑偱偼丄掕媊偲偄偆傛傝偼墌傪F幆硞箓閭苽陚蓚▊膩A帇妎丄怗妎偲偄偆姶妎偺柺偱巜摫偣偞傞傪摼側偔丄愗傝敳偐傟偨宍偲偟偰偺恾宍揑側懆偊曽偲側傞丅偙傟偑崅峑偵側傞偲丄偡偙傇傞奣擮揑側僆僽僕僃僋僩偵曄梕偡傞丅墌偼丄敿宎偲拞怱偲偄偆梫慺偑梌偊傜傟偨偲偒偺揰偺婳愓偱偁傝丄 側傞曽掱幃偑昞傢偡傕偺偼丄墌偺旂(墌廃)偱偁傝拞恎偼敳偗棊偪傞丅嶰妏宍傕慠傝丄曻暔慄傕慠傝丅梫偼恾宍偦偺傕偺偑偳偆戙悢揑偵昞尰偝傟傞偐偲偄偆偙偲偑榑揰側偺偱偁傞丅
丂偝偰丄乽擄偟偄栤戣偱偡偹偉乿偲媈栤傪搳偘偐偗偰偄傞偺偼拞妛峑偺愭惗丅偦偺棫応偼幚偵旝柇偱偁傞丅嬶徾奣擮揑側恾宍偲偟偰偺墌偐傜拪徾奣擮揑側婳愓偲偟偰偺墌傊偺嫶搉偟傪偟偰偄傞偺偑拞妛偱偁傝丄惗搆偺屄乆偺惛恄揑敪払傪峫椂偟側偑傜偺巜摫偲側傞丅偦傟偼丄惗搆偺棟夝椡塢乆偲偄偆傛傝丄擼偺憐憸揑側椞堟偺嫋梕検偺栤戣偱偁傞丅塃擼偼姶妎擼偲偄傢傟傞偑丄偦偺椞堟偱偺墌偺擣幆偼梕堈偱偁傝丄側傫傜栤戣傕側偄丅偟偐偟丄埨堈偵擣幆偱偒傞偐傜偙偦丄榑棟揑巚峫擼偲偟偰偺嵍擼傊偺愗懼偊偑崲擄偵側傞丅偦偆偟偰丄偄偮傑偱傕塃擼偵偟偑傒偮偄偰偄傞偲丄榑棟揑偵柌尒傞偙偲傪嵍擼偑榑棟揑偵嫅愨偟偰偟傑偆偺偱偁傞丅偦偺僞僀儈儞僌傪屄乆偺惗搆傪娤嶡偟側偑傜悇偟検傝丄巜摫偡傞偙偲偼惛恄柺偱偺掅擭楊壔偑嫨偽傟傞拞丄嬌傔偰偦偺敾抐偑擄偟偔戝曄側偺偑尰忬偱偁傠偆丅偝偰丄忳傟傞傕偺偲忳傟側偄傕偺傕偙偺娭學偵帡偰偄傞丅曻暔慄偲偄偆恊偟傒傗偡偄尵梩偼偄偮偺娫偵偐乽擇師娭悢偺僌儔僼乿偵僨僼僅儖儊偝傟丄曻暔慄偺曄壔偑偳偆擇師娭悢偺奺崁偺學悢偵娭梌偡傞偺偐偑偦偺僥乕儅偲側偭偰偄傞丅椉嬌偵埵抲偟偰偄傞姶妎揑側曻暔慄偲榑棟揑側擇師娭悢偼丄僶儔儞僗傪庢傝側偑傜栤戣夝寛偺拞偱憃曽岦偵峴偒棃偟丄偦偺揤鈍偺幉傪扴偭偰偄傞偺偑暯曽姰惉偺曄宍側偺偱偁傞丅偩偐傜偙偺晹暘傪忳傞偙偲偼丄榑棟偲姶妎傪暘抐偡傞偙偲偱偁傝丄偦偺寢壥丄惗搆偺嫵嵽偵懳偟偰偺嫽枴丄堄梸偼媫懍偵椻偊崬傫偱偟傑偆丅
丂偦偺忳傟側偄暯曽姰惉偺巜摫偺拞偵傕丄姶妎揑側晹暘偲榑棟揑側晹暘偑偁傞傛偆側婥偑偡傞丅椺偊偽丄棟憐揑曄宍朄偼榑棟揑巚峫偺怓崌偄偑嫮偄丅偩偑丄偙偺榑棟揑巚峫偵傕姶妎揑側梀傃偺晹暘偑側偄偲暯曽姰惉偺嶌嬈偼堄梸偺柺偱峴偒媗傑偭偰偟傑偆丅偙傟偵懳偟丄僗儕儉揑曄宍朄偺乽敿暘堷偔擇忔乿偼丄姶妎擼偵慽偊傞尵梩偺梀傃偱偁傝丄椉曈傪俀師偺崁偺學悢偱妱傝丄嶌嬈偺扨弮壔丄岠棪壔偡傞偙偲傕丄塃擼傊偺摥偒偐偗偺傂偲偮偲偄偊傞偩傠偆丅偦偆偟偰栤戣偺杮幙傪僗儕儉壔偟側偑傜丄榑棟揑偵暯曽姰惉傪扏偒崬傫偱偄偔丅僗儕儉揑曄宍朄偼姶妎揑巚峫偺傕偺偲偄偊傞丅偩偑丄偙偺曄宍朄偑丄悢妛榑棟偺拞偱堦娧惈傪曐偰傞偐偳偆偐偼媈傢偟偄丅
丂嵟廔揑偵偼丄
偲偄偆僟僀儗僋僩揑側曄宍偱側偗傟偽栤戣夝寛傊偺忈奞偑偳偙偐偵巆傞偺偱偁傞丅偙偺曄宍偼丄棟榑偑惉挿偟偨抦妎偺傕偺偲偄偊傞丅
丂僗儕儉揑曄宍朄偱偼丄俆寧昦偲偲傕偵巒傑傞暯曽姰惉巜摫偵偍偗傞嫵巘偺嬯擸偑丄傎傫偺彮偟愭憲傝偝傟偨偩偗側偺偐傕偟傟側偄丅