交わらない２円の交点を通る直線の存在

－北数教数実研の試み－

埼玉大学　岡部　恒治，　　札幌新川高校　中村　文則

０．はじめに

　一昨年の秋、岡部は、中村より北数教（北海道算数数学教育会）数実研のホームページ『数学のいずみ』の存在を知らされました。そこで、同じ問題を別の（しかも興味深い）切り口で研究しているグループがあることを知りました。これをまとめようと話していたのですが、種々の事情で遅くなり、間もなく次期指導要領の発表が迫っています。そこで、高校の数学のありかたとからめてお話しします。以下の文は１～３は岡部が、４以降は中村が担当しています。なお、このような研究実践活動は北数教の他にもあるでしょうし、既に同じことを発表していた方がいるかもしれません。この文が『数セミ』でのいろいろな活動紹介のきっかけになれば、とも思います。

１．受験数学は誰が作ったか

　発端は『数学のいずみ』に中村が掲載した、以下の刺激的な文である。

「２つの円
　　x2+y2=1　　………①　　　 　　x2+y2-6x-8y+16=0　　………②
の交点を通る直線は何か」
という問題を、①－②より
　　6x+8y-17=0
としてしまうのは、テクニック偏重の受験数学の最たるものである。」 　実は、この後にこの直線の意味について、さまざまな検討が加えられる。このことが主要なテーマですが、この文章から派生した問題もコメントすべきでしょう。

　この文の中の「受験数学」について、ＳＥＧの古川昭夫氏が「これは教え方だけの問題ではないのか。受験数学というものが本当にあるのか？あるとしたら、それを作ったのは誰？」という鋭く的を射た問いかけを発しました。それからいろいろと論争がありました。この中で、岡山大付属中の川上公一氏の次の意見を特に明記しておきます。｢ここから授業が始まると思う」。中村が問いかけたのも、「そこで終わるのは問題だ」という意味で、まさしく同じ意見なのです。

　これに関連して、ちょっと気になるのは、大学人の数学の内容に触れない｢受験数学」への非難です(例えば本誌９月号の巻頭言)。受験の数学は、高校での数学の理解を問うもので、数学の内容に問題がなければ、これがおかしいのは、試験のしかたが悪いことになるでしょう。それを出題している側の｢受験数学｣への非難は論理的に成り立たないと思います。

　一番の問題は、｢受験数学｣という名前によって、｢そんなものはやらなくとも良い｣として、高校生を数学から遠ざけてしまうことです。

２．責任はどこに

　今の話に関連して、本誌12月号の｢次期カリキュラムはどうなるか｣の記事も気になりました。そこには、教課審の会議で秋山委員が「(数学の教科の)３割削減を決定した責任を我々に負わせないように」と噛みついたとあります。秋山委員の気持ちはよくわかるのですが**)、むしろ教課審の責任を明確にすべきではないでしょうか。責任の所在が曖昧のままでは、何年かたって技術力が落ちたときに、数学者や現場にその責任を転嫁されるのが見えています(共通一次試験導入に熱心だった元首相が、後に｢こんな画一テストはけしからん｣と述べた例もあります)。あるいは、｢受験産業｣という仮想敵に矛先をもっていくことも考えられます。

　とかく教育問題は、リアリティのない議論が横行しています。その最大の原因は、責任の転嫁です。

**)しかし，朝日新聞（6月23日付）での3割削減に肯定的ともとれるインタビュー記事との落差はいまだに理解できない。


３．二円の接点までの距離が等しい点の軌跡

　さて、川上先生の意見に同意したのは、高校の｢受験数学｣と思われている部分にも、おもしろい問題が隠されていると言う意味です。その点では、この｢２つの円の交点を通る直線の問題｣はさまざまの切り口があり、まさに「ここから授業が始まる」良い例だと思います。まずは、数学の先生に「数学はおもしろい」と思ってほしいのです。

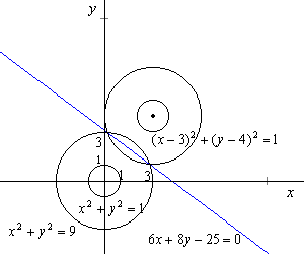
　ようやく、本題に戻りました。この問題について私が最初に考えたのは、センター試験問題の解答を書いているときでした。２つの円の半径が等しいときの、２円の対称線の直線の式を求める問題です。例えば、

x2+y2=1　　………③　　　 　　x2+y2-6x-8y+24=0　　………④
はともに半径１の円である。対称線の方程式を求めよ。

がそうです。これも③－④で計算した
　　6x+8y-25=0
となります。

　もちろん、面倒な計算をすれば、③－④で出る理由はつけられるので、そのままにしていました。

　その後、５年前に開かれた筑波大の公開講座「数学を深く楽しく学ぼう」(責任者吉田稔氏)に参加して、筑波大付属高校の利根川誠氏による方程式の解と作図の講義を中高生と一緒に聴く機会がありました。この講義では、かなり代数的に作図を扱っていましたが、この講義で提出された問題の別解を考えているうちに、 ③－④の意味が見えてきました。

　つまり、さきほどの問題は③と④の右辺に同じ数を加えて、二円の半径を同時に大きくすれば２交点を通る直線の式で、それが③－④の計算で良かった理由だったのです。
右辺に8を加えて、円の半径を3にしたとき

　さて、一般の場合も、同じことが言えます。最初の二円の式①、②の右辺に適当な数 を加えて、
　　x2+y2=1+r2　　………①´
　　x2+y2-6x-8y+24=r2　　………②´

　こんどは交わるようにします(図参照)。そうすると、
　　①－②=①´－②´　となっています。

　この直線上の点Pは(円の外では)、｢①´と②´へPから接線を引いたときに、Pからそれぞれの接点までの距離が等しい｣という条件を満たす点でもあります。つまり、図では、PT=PSとなっています。

　これは①と②の関係では、PU＝PVも示せます。つまり、①－②から出てくる直線の式は、｢①と②へPから接線を引いたときに、Pからそれぞれの接点までの距離が等しい｣ということなのです。これが、二円がたまたま交わったときには、交点を通る直線になっているだけのことだというわけです。

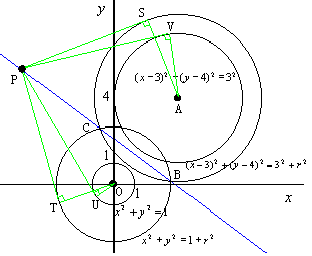　三平方の定理より
　　PT2=PO2+(1+r2)
　　PS2=PA2+(32+r2)

一方、方べきの定理から
　　PT2=PB･PC=PS2
　　　∴　PO2+(1+r2)=PA2+(32+r2)
　　　∴　 PO2+1=PA2+32
　　　∴　 PU2=PV2




４．空間内の２曲線の交線の影

　視点を変えてみましょう。①,②の右辺に加えた増分z2を空間におけるz成分とみます。
　　x2+y2=1+z2　　………④
　　x2+y2-6x-8y+16=z2　　………⑤
　このとき曲線は、[fig A]のように、z軸方向に双曲面を描き、2曲線の交わりである双曲線のxy平面への射影が求める直線であることが分かります。同様に、増分をzとしたのが[fig B]で、放物面を描きます。

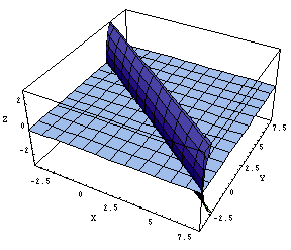
　2円の差から得られる直線6x+8y-17=0は、このように空間的には2曲線の交わりを表す曲線のxy平面への射影とみることで、説明がつけられます。
[fig A][fig B]
　一般に空間内の２つの曲線を
　　　f(x，y，z)
　　　g(x，y，z)
とすれば、このとき、
　　　f(x，y，0)=x2+y2-1
　　　g(x，y，0)=x2+y2-6x-8y+16
であれば、同様の直線が得られます。
　　　h(x，y，z)=f(x，y，z)-g(x，y，z)
に対して、
　　　g(x，y，0)=6x+8y-17
となればよいわけですから、必ずしも、交わりを表す曲線のｘｙ平面への射影を考える必要もないことになります。すなわち、
　　　x2+y2=1+z2　　………⑥
　　　x2+y2-6x-8y+16=z　　………⑦
のとき、⑥－⑦から得られる
　　　6x+8y-z2+z-17=0
とxy平面との交線とみても良いのです。[fig C]

[fig C]

５．2球面の交わりとして

　ところで、この２円の交線の問題は、３年前、北数教数実研の夏季セミナーで話題になったものでした。

「2円が交わっていなくとも、2円の方程式の差をとると、直線の方程式が得られるが、この直線は何を意味するか。」
　生徒の単純な疑問が始まりです。得られた直線を原式の円に代入すると、方程式は虚数解となりますから、直線上の点 は虚数の組です。存在しない直線の存在が要求されたわけです。数学的(代数的)にはいろいろな説明がつけられますが、教育的にはどう解釈されるべきでしょう。

　次のようなアプローチが報告されました。

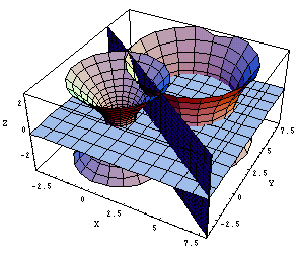
　交わらない2円を、空間内の2球面とxy平面との交線と考えます。
　　　f(x，y，z)=x2+y2+z2-2az-1
　　　g(x，y，z)=x2+y2-6x-8y-2az+16
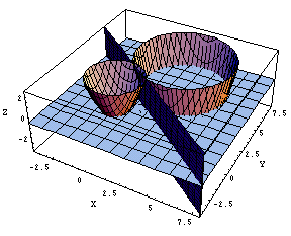
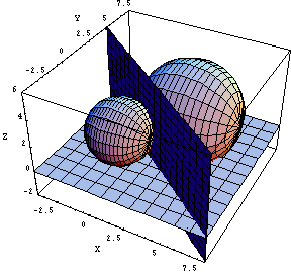
　このとき、f(x，y，z)=0、g(x，y，z)=0 で表される2球面において、a→∞とすると、その交わりを表している円の半径は増加し、円弧はxy平面に近づき、直線6x+8y-17=0に近似していきます。

　球面という身近な空間素材から、イメージが膨らみ、円弧が直線になってｘｙ平面上に落ちていく様子が連想できればと思います。［fig D］

[fig D]

６．虚円のイメージ化

　さらに、研究会では、xy平面を複素化し直線の影を探る試みが早苗雅史氏(札幌稲北高校教諭)により報告されました。

　簡単のために２つの円を次のようにします。
　　　C1：x2+y2=1　　………⑧
　　　C2：(x-3)2+y2=1　　………⑨

　ここで、x∈R、y∈Cとし、
　　　y=u+vi　(u，v∈R)
とおきます。⑧に代入し整理すると、
　　　(x2+u2-v2)+2uvi=1
　　　∴x2+u2-v2=1　　(一葉双曲面)
　　　uv=0　　　(二平面)

　同様にyを⑨に代入すると
　　　(x-3)2+u2-v2=1（一葉双曲面）
　　　uv=0　　　(二平面)
が得られます。

　これから、u=0(xy平面)では、
　　　x2+v2=1，　　(x-3)2-v2=1　　（二双曲線）

　また、v=0(xy実平面)では、
　　　x2+u2=1，　　(x-3)2+u2=1　　(二円)
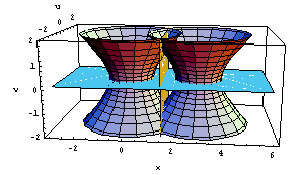
を表し、これらの曲面と平面を同時に描画したのが、[fig Ｅ]となります。平面v=0(xy実平面)ではもともとの2円C1とC2は交わっていませんが、yが虚数であるとき、xv平面上では双曲線が広がり、その交線の影が、2円の差として得られる平面x=2/3の一部として、浮かび上がってくることがわかります。[fig Ｅ]

[fig E]

７．数学感の視覚化

　二円の交線問題は、数学と教育学の間の多くの人達に論議され、研究会では疑似虚平面の説明により一応の収束をみました。論議を呼んだ理由はそれが(高校生に対しての)数学的な難しさと面白さを併せもっているからです。二円の差として得られる直線上の点(x，y)を虚数の組とみて４次元を構築することは無理でも、曲線の交線の影と捉えることは可能です。

　こういった教育学的側面からのアプローチが高校から大学の数学の架け橋(これを受験数学というのでしょうか)を面白いものとしていくのだと思います。今回の場合、その討論の場を提供したのはネットワーク型教材データベース「数学のいずみ」やインターネット上の仮想会議(バーチャルコンファレンス)でした。インターネットを通したオンラインの数学アイデアの相乗りは、閉塞的傾向にある数学教育をビジュアルに変革していくのかもしれません。

＊このレポートは「1999年 数学セミナー 2月号」に掲載されたものを，ホームページように作成しなおしたものです。